【原创】二分图匹配 与 匈牙利算法

二分图

先来看看什么是二分图。

二分图的概念

部图

在了解二分图之前，我们现在看看图论中的部图。
部图在图论中有这样的定义：

一个图的节点集可分成若干个子集，使得每一条边的两端点不在同一子集内.若一个图的节点集能分成k个两两不交的非空子集，使得这个图的每一条边的两端点不在同一个子集内，则称其为k部图。如果
k=2时，称为2部图，k=3时，称为3部图。特别的，称2部图为偶图。
如果每一个部中每一个顶点都与其他部的所有顶点都有连边，则称其为完全k部图。

比如下图：

就是一个偶图。

是三部图。

是完全偶图。

像这种，只能一个点一部，是六部图。

简而言之，部图就像老师把班级（图）分组（分部）。有些学生（点）之间会讲话（连边），老师肯定不希望他们分在同一个组，所以老师就把班级分成了k组，这k组中每个人都不会讲话（没有边）。这就叫k部图。
（尽管这种状况基本不会发生）

在编程里，二分图就是偶图。我们称其中一部为X部，相对的，另一个部就称为Y部。

二分图的性质

定理Ⅰ：

一个无向二分图所有回路的长度必为偶数。

这是一个图为二分图的充要条件。

证明：

必要性：
设二分图G里，有任意一个回路C{v0,v1,v2,…,vk}。
根据二分图定义：这些点必定轮流出现在X部，Y部。
因为C是回路，所以vk和v0一定在同一个部。
不妨设{v0,v2,v4,….,vk}在X部，{v1,v3,v5,….,vk-1}在Y部。
因此k必为偶数。

充分性的证明较为复杂，请读者查看以下链接：二分图。

二分图的判定

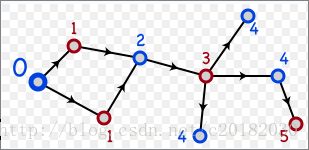
如上图，在一个连通图中，任选一个顶点v，定义一个距离编号d，置d[v]=0，然后把它的邻接点的编号置为1。对于所有d为1的顶点，它的所有邻接点（若未被编号）的d置为2。以此类推。
这个过程可以用一次BFS实现。
BFS结束后，依次搜索每一条边，若它的两个端点编号的奇偶性相同，那么该图一定不是二分图。
搜索结束后，如果每条边都满足，那么它就是二分图。
不是连通图，在每一个连通块里进行判断。

二分图匹配

匹配的概念

在一个二分图G里，挑选一个子图M，如果M的边集{E}中所有的边都不依附于相同的顶点，则称M为G的一个匹配。其中边集里边的数量称为这个匹配的数量。

说简单点，就是挑选一些边，这些边的顶点都不同，这就是匹配。
如图，就是一个数量为3的匹配。

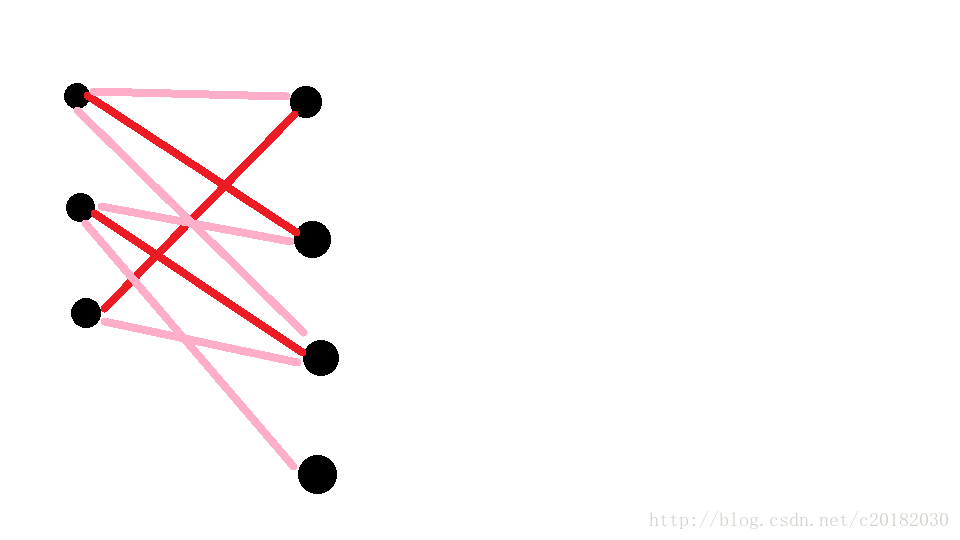
当然，任意一个二分图里，匹配不唯一。

最大匹配与完全、完备匹配

最大匹配

一个二分图内数量最大的匹配称为最大匹配，即参与匹配的边最多。

完全匹配与完备匹配

一个二分图内，如果每个顶点都参与了匹配，则称这个匹配为完全匹配，也叫完备匹配。

那么，怎么找最大匹配呢？
别急，我们先来看看什么是增广路径。

增广路径

增广路径的定义

对于任意一个匹配M，P是二分图G中连接两个未匹配顶点的路径（两点属于不同部），如果这条路径上，∈M与∉M的边交替出现，则称P为M的一条增广路径，也叫交错轨。

根据定义，我们可以总结出增广路径的三大条件：

1. 连接两个未匹配的顶点的的路径。（可以是一条又一条拼凑起来的一条路径）
2. 这两个顶点分属两部。
3. 匹配边与未匹配边交替出现。
   如图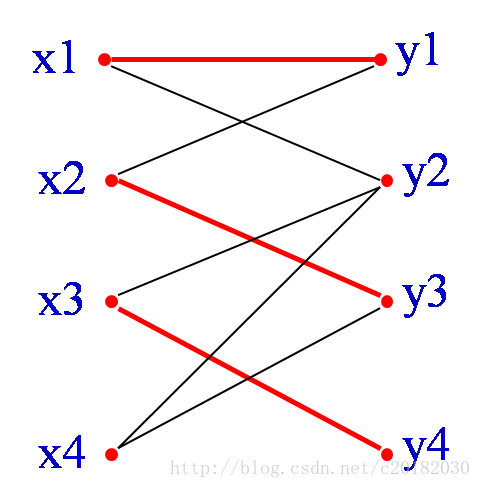，，从X部未匹配的顶点x4出发，x4→y3→x2→y1→x1→y2就是一条增广路径。

增广路径的性质

定理Ⅱ ：

增广路径的长度一定是奇数。

证明：

假设这条增广路径从X部出发，到Y部结束，途径点集{a1,b1,a2,b2,…..,ak,bk}。
因此，一定会途径偶数个点，因此它的长度一定为2k-1，是个奇数。
Q.E.D.

定理Ⅲ

对增广路径取反，可以得到一个更大的增广路径。当图中没有增广路径时，一定是最大匹配。

这个定理的证明很简单，因为增广路径有奇数条边，而且是先选的未匹配的边，因此取反以后（即把路径上不在匹配里的组成一个匹配，原来的那个匹配的踢出匹配），匹配里的边一定会+1。
由此可以想到一个递归的算法，不断地找增广路径，然后不断地取反，然后就可以找到最大匹配了。

匈牙利算法

提出者与历史

1965年由匈牙利科学家Edmonds提出，因此被称为匈牙利算法，是一种求二分图最大匹配的算法。

原理与基本流程

上文已经提过，大致的流程是这样的：

(1)置M为空
(2)找出一条增广路径P，通过取反操作获得更大的匹配M’代替M
(3)重复(2)操作直到找不出增广路径为止

算法的实现

找增广路径

我们决定用dfs来找增广路径。
从X部一个未匹配的顶点u开始，找一个未访问的邻接点v（v一定是Y部顶点）。对于v，分两种情况：
(1)如果v未匹配，则已经找到一条增广路
(2)如果v已经匹配，则取出v的匹配顶点w(w一定是X部顶点)，边(w,v)目前是匹配的，根据“取反”的想法，要将(w,v)改为未匹配，(u,v)设为匹配，能实现这一点的条件是看从w为起点能否新找到一条增广路径P’。如果行，则u-v-P’就是一条以u为起点的增广路径。

因此我们可以大致写出一个伪代码：

cx[i]表示与X部i点匹配的Y部顶点编号
cy[i]表示与Y部i点匹配的X部顶点编号
bool dfs(int u)                       //寻找从u出发的增广路径
{
     for each v∈u的邻接点
        if (v未访问)
         {
                标记v已访问;
                if (v未匹配 || dfs(cy[v]))
                {
                    cx[u] = v ;   cy[v] = u ; 
                    return true;        //有从u出发的增广路径
                 }
          }
       return false;                    //无法找到从u出发的增广路径
}
void EK( ) 
{
     int ans = 0 ;
     memset(cx , 0xff , sizeof(cx)) ; memset(cy , 0xff , sizeof(cy)) ;
     for (int i = 0 ; i <= nx ; i++) 
        if (cx[i] == -1) //如果i未匹配
        { 
            memset(visit , false , sizeof(visit)) ; 
             ans += dfs(i) ; 
        }
       return ans ;
} 

匈牙利算法的代码

使用邻接矩阵：

bool dfs(int R)
{
//CR[i][j]是邻接矩阵，如果i,j有边，则CR[i][j]为1
//C是这条增广路径
    for(int i=1;i<=n;i++)
    {
        if(CR[R][i] && !vis[i])
        {
            vis[i]=1;
            if(C[i]==0 or dfs(C[i]))
            {
                C[i]=R;
                return 1;
            }   
        }
    }
    return 0;
}
void EK()
{
    int ans=0;
    for(int i=1;i<=n;i++)
    {
        memset(vis,0,sizeof vis);
        if(dfs(i)) ans++;
    }
    printf("%d\n",ans);
}

匈牙利算法的时空分析

时间复杂度：
dfs()：邻接矩阵： O(n²)，邻接表：O(n+m)
EK() : 邻接矩阵：O(n³) , 邻接表：O(n*m)

空间复杂度：
邻接矩阵：O(n^2)
邻接表： O(m+n)

最大匹配与最小点覆盖

最小点覆盖的定义

在二分图中挑选一个点集，使得这些点与这些点的直接邻接点覆盖整个点集。

könig定理

在一个二分图中，最小点覆盖的数量等于最大匹配的数量。

证明：

事实上，你只需要在最大匹配里，每条边挑一个顶点，就可以覆盖全图了。

如果觉得这个证明太水，想看具体证明，可以点击这里。
以下证明也转自这个网站：http://www.matrix67.com/blog/archives/116。

假如我们已经通过匈牙利算法求出了最大匹配（假设它等于M），下面给出的方法可以告诉我们，选哪M个点可以覆盖所有的边。
匈牙利算法需要我们从右边的某个没有匹配的点，走出一条使得“一条没被匹配、一条已经匹配过，再下一条又没匹配这样交替地出现”的路（交错轨，增广路）。但是，现在我们已经找到了最大匹配，已经不存在这样的路了。换句话说，我们能寻找到很多可能的增广路，但最后都以找不到“终点是还没有匹配过的点”而失败。我们给所有这样的点打上记号：从右边的所有没有匹配过的点出发，按照增广路的“交替出现”的要求可以走到的所有点（最后走出的路径是很多条不完整的增广路）。那么这些点一定组成了最小覆盖点集。
首先，为什么这样得到的点集点的个数恰好有M个呢？答案很简单，因为每个点都是某个匹配边的其中一个端点。如果右边的哪个点是没有匹配过的，那么它早就当成起点被标记了；如果左边的哪个点是没有匹配过的，那就走不到它那里去（否则就找到了一条完整的增广路）。而一个匹配边又不可能左端点是标记了的，同时右端点是没标记的（不然的话右边的点就可以经过这条边到达了）。因此，最后我们圈起来的点与匹配边一一对应。
其次，为什么这样得到的点集可以覆盖所有的边呢？答案同样简单。不可能存在某一条边，它的左端点是没有标记的，而右端点是有标记的。原因如下：如果这条边不属于我们的匹配边，那么左端点就可以通过这条边到达（从而得到标记）；如果这条边属于我们的匹配边，那么右端点不可能是一条路径的起点，于是它的标记只能是从这条边的左端点过来的（想想匹配的定义），左端点就应该有标记。
最后，为什么这是最小的点覆盖集呢？这当然是最小的，不可能有比M还小的点覆盖集了，因为要覆盖这M条匹配边至少就需要M个点（再次回到匹配的定义）。
证完了。