机器学习经典算法-决策树学习之ID3算法

机器学习经典算法-决策树学习之ID3算法

简介

　　决策树是一种常用的分类方法，他是一种监督学习，首先给定一些实例样本，每个样本都有一组属性和一个事先确定的类别，通过学习得到一个分类器，这个分类器能够对新出现的实例给出其分类。
　　下图给出一棵典型的决策树，这棵决策树根据天气情况分类是否适合“打网球”（机器学习Tom M.Mitchell）。

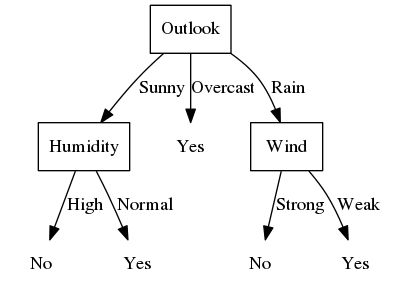
　　通常决策树代表实例属性值约束的合取的析取式，上例表示的决策树对应于

(Outlook＝Sunny⋀Humidity=Normal)⋁(Outlook=Overcast)

⋁(Outlook=Rain⋀Wind=Weak)

对于实例

<Outlook=Sunny,Temperature=Hot,Humidity=High,Wind=Strong>

将沿着 Outlook→Humidity→No 的路径得到该天气不适合打网球。

本文数据集（出自机器学习Tom M.Mitchell）如下：

Outlook	Temperature	Humidity	Wind	PlayTennis
Sunny	Hot	High	Weak	No
Sunny	Hot	High	Strong	No
Overcast	Hot	High	Weak	Yes
Rain	Mild	High	Weak	Yes
Rain	Cool	Normal	Weak	Yes
Rain	Cool	Normal	Strong	No
Overcast	Cool	Normal	Strong	Yes
Sunny	Mild	High	Weak	No
Sunny	Cool	Normal	Weak	Yes
Rain	Mild	Normal	Weak	Yes
Sunny	Mild	Normal	Strong	Yes
Overcast	Mild	High	Strong	Yes
Overcast	Hot	Normal	Weak	Yes
Rain	Mild	High	Strong	No

决策树适用的问题
- 实例是由“属性-值”对表示的
- 目标函数具有离散的输出值
- 可能需要析取的描述
- 训练数据可以包含错误
- 训练数据可以包含缺少属性值的实例

　　本文试图实现一个简单的决策树算法，因而并不能涵盖以上所有的范围，尤其是最后两条，事实上，本文最终的实现要求数据不包含错误且属性和目标输出都是离散的值。

用信息增益确定最佳分类属性

　　ID3算法的核心问题是如何选取一个最佳的分类属性，也就是为什么上图所举的例子要选取Outlook作为第一层的分类属性。ID3算法采用一种称为“信息增益（information gain）”的统计属性来衡量各个属性区分训练样例的能力。
　　为了学习信息增益，首先需要了解信息论中广泛应用的一个概念：熵（entropy）。熵用来度量事物的无序性，比如某个属性的值全部相同，它的熵就是0，一般的，如果目标属性具有c个不同的值，那么集合S相对于c个状态的熵定义为：

Entropy(S)=∑i=1c−pilog2pi

其中 pi 是S中第i类属性值占的比例。
　　信息增益描述的就是数据集合S以某个属性A分类而导致的熵的降低，其定义为：

Gain(S,A)=Entropy(S)−∑v∈Value(A)|Sv||S|Entropy(Sv)

其中 Sv 是S中属性A的值为v的子集 Sv={s∈S|A(s)=v} ， Values(A) 是属性A所有可能值的集合。
　　以上述数据为例，用S表示数据集，S中目标属性包含5个 No 和9个 Yes ，则 Entropy(S)=Entropy([9,5])=−(9/14)log2(9/14)−(5/14)log2(5/14)≈0.940 ，如果以属性Outlook进行分类，则每个类别包含的目标属性个数如下：

PlayTennis	yes	no
Sunny	2	3
Overcast	4	0
Rain	3	2

　　所以Entropy(SSunny)=−(2/5)log2(2/5)−(3/5)log2(3/5)=0.971，同理Entropy(SOvercast)=0， Entropy(SRain)=0.971。
　　

Gain(S,A)=Entropy(S)−∑v∈Value(A)|Sv||S|Entropy(Sv)

≈0.940−514∗0.971−414∗0−514∗0.971≈0.247

　　同理可得其他属性的信息增益

属性	Outlook	Temperature	Humidity	Wind
信息增益	0.247	0.029	0.152	0.048

由于根据属性Outlook进行分类可以使得数据集的信息熵下降最快，因此采用属性Outlook进行第一步的分类。

决策树学习算法描述

算法描述如下：

ID3(data, target, attr)
    创建root结点
    如果所有数据目标属性一致，则返回值为该属性值的叶结点
    如果attr为空，则返回叶结点，值为数据中目标属性最普遍的值
    否则，做以下步骤
        在attr中找出分类能力最好的属性A
        对于属性A的每个可能的值ai
            增加一个新的子树，对应于A = ai
            令data_i为data中满足A的属性值为ai的子集
            如果data_i为空
                子树包含一个叶结点，值为data中目标属性最普遍的值
            否则，子树为ID3(data_i, target, attr - {A})
    返回root

算法实现

　　原则上来说，本节应当是上一节的内容，单独分出本节出自于以下考虑：

1. 代码是作者根据机器学习（Tom M.Mitchell） 上的描述和自己的想法实现的，可能与原算法有所出入；
2. 测试样例只有一个，不能保证代码的正确性；
3. 如果读者有自己的思路，那么阅读作者的代码会大大限制读者的想象力；
4. 代码简介如下。

决策树结点结构体

class ID3_Node
{
    int    attr_index; // 属性下标
    int    target_value; // 如果该结点为叶结点，则保存属性的值
    double gain; // 信息增益

    std::vector child; // 子结点的指针
    friend class ID3;
};

保存了最基本的内容，未设置接口，而是将ID3 设置为友元类，方便访问数据，但不建议这样做。

ID3 算法的主类

class ID3
{
    typedef std::vector<std::string>            vs;
    typedef std::vector                     vvs;
    typedef std::vector<int>                    vi;
    typedef std::vector                     vvi;
    typedef std::unordered_map<std::string,int> usi;
    typedef std::vector                    vusi;
private:
    std::string target_attr;  // 目标属性
    vs          headers;      // 各个属性的名称
    vvi         datas;        // 将属性映射到整数后的数据集，并按列保存
    vusi        attr_to_int;  // 属性到整数的映射
    vvs         int_to_attr;  // 整数到属性的映射
    vi          attrs_size;   // 每个属性有多少个不同的属性值
    int         num_attr;     // 属性数量
    int         num_data;     // 数据集大小
    int         target;       // 目标属性在headers中的下标
    ID3_Node*   root;         // 决策树根结点指针
    const static double log2;

    // ... functions
};

　　类型的数据部分，其中大部分的注释可以表明数据的作用，主要思路就是将以字符串形式表示的属性值映射成整数类型，便于保存和计算，假设属性值的个数远远小于数据集的大小。datas按列保存的意思是，datas[i][j] 表示第j条数据的第i个属性值，进行颠倒是因为一般进行访问所有数据的某一个属性，这样可以使得访问位于临近的内存区域。
　　将函数省略是因为：没有原因。

开始构建决策树

ID3_Node* ID3::_build_tree(const vi& data_list, const vi& attr_list)
{
    // 当前数据集中的一个目标属性值
    auto      &dl           = data_list;
    auto      &al           = attr_list;
    int       one_of_target = datas[target][dl[0]];
    ID3_Node* node          = new ID3_Node;
    bool      flag          = std::all_of(dl.begin(), dl.end(),[&](int x)
            {
                return (datas[target][x] == one_of_target);
            });

    // 如果当前数据集所有目标属性相同，则建立一个叶子结点
    if(flag)
    {
        node->attr_index   = target;
        node->target_value = one_of_target;
        node->gain         = 0;
    }
    // 如果当前属性值为空，则建立一个叶结点
    // 值为当前数据集中出现次数最多的目标属性值
    else if(al.empty())
    {
        node->attr_index = target;
        vi tmp;
        tmp.resize(attrs_size[target], 0);
        for(auto& i : dl)
            ++tmp[datas[target][i]];
        int max_index = -1, max_value = -1;
        for(int i = 0; i < (int)tmp.size(); ++i)
            if(max_value < tmp[i])
                max_value = tmp[i], max_index = i;
        node->target_value = max_index;
        node->gain = 0;
    }
    else
    {
        // 使用最好的属性来建立分支
        double current_gain;
        int best_attr    = _find_best_attr(dl, al, current_gain);
        node->attr_index = best_attr;
        node->gain       = current_gain;
        int attr_size    = attrs_size[best_attr];

        // 按照属性值分离数据集
        vvi data_i;
        data_i.resize(attr_size);
        for(auto& x : dl)
            data_i[datas[best_attr][x]].push_back(x);

        for(int i = 0; i < attr_size; ++i)
        {
            ID3_Node* p = nullptr;

            // 如果当前属性值对应的数据集为空，建立叶结点
            // 值为原数据集中出现最多的目标属性的值
            if(data_i[i].empty())
            {
                vi tmp;
                tmp.resize(attr_size, 0);
                for(auto& x : dl)
                    ++tmp[datas[target][x]];
                int max_index = -1, max_value = -1;
                for(int k = 0; k < attr_size; ++k)
                    if(max_value < tmp[k])
                        max_value = tmp[k], max_index = k;

                p               = new ID3_Node;
                p->attr_index   = target;
                p->target_value = max_index;
                p->gain         = 0;
            }
            else
            {
                // 分支结点的属性列表
                vi attr_i;
                for(auto& j : al)
                    if(j != best_attr) attr_i.push_back(j);
                p = _build_tree(data_i[i], attr_i);
            }

            node->child.push_back(p);
        }
    }

    return node;
}

以上是按照上一节的算法描述实现的，基本上每处注释对应算法描述中的一句话，如果看懂了算法描述的话，这里还是不难理解的。

寻找最佳分类属性

遍历当前属性列表，找到使得信息增益最大的属性值

/*
 *
 * function: _find_best_attr 查找当前最优的属性
 * data_list: 当前数据集
 * attr_list: 当前属性集
 * current_gain: 保存最优属性对应的增益值
 *
 */
int ID3::_find_best_attr(const vi& data_list, 
        const vi& attr_list,
        double& best_gain)
{
    best_gain = -1;
    int best_attr = -1;
    for(auto &attr : attr_list)
    {
        double current_gain = _gain(data_list, attr);
        if(best_gain < current_gain)
            best_gain = current_gain, best_attr = attr;
    }
    assert(best_attr != -1);
    return best_attr;
}

计算每个属性的信息增益

/*
 * function: ID3::_gain 获取以当前属性进行分支对数据集的增益
 * data_list: 数据集
 * attr: 属性
 *
 */
double ID3::_gain(const vi& data_list, int attr)
{
    double entropy_S = _entropy(data_list);
    double data_size = (double)data_list.size();
    // 按照当前属性将数据集分成子数据集
    vvi data_i;
    data_i.resize(attrs_size[attr]);
    for(auto& j : data_list)
        data_i[datas[attr][j]].push_back(j);
    // 求信息增益
    double sub_entropy = 0;
    for(int i = 0; i < (int)data_i.size(); ++i)
        sub_entropy += data_i[i].size() * _entropy(data_i[i]) / data_size;

    return entropy_S - sub_entropy;
}

计算每个属性值的熵

/*
 * function: ID3::_entropy 计算数据集的熵
 * data_list: 数据集
 *
 */
double ID3::_entropy(const vi& data_list)
{
    double entropy_sv = 0;
    double data_size = (double)data_list.size();
    vi tmp;
    tmp.resize(attrs_size[target], 0);
    for(auto &j : data_list)
        ++tmp[datas[target][j]];
    for(int i = 0; i < (int)tmp.size(); ++i)
    {
        if(tmp[i] != 0)
        {
            double d = tmp[i] / data_size;
            entropy_sv -= d * log(d) / log2;
        }
    }
    return entropy_sv;
}

输出结果

　　树形结构不方便直观地展示。代码实现了两种输出。

最简单的表示方法
root
.son1
..grandson1
..grandson2
.son2
.son3

使用dot语言保存
dot文件是一个文本文件，描述了图表的组成元素以及它们之间的关系，具体可以使用搜索引擎搜索Graphviz，本文第一张示例图就是这样画出来的。

小结

　　本文实现的程序没有考虑属性值为连续的情况，而C4.5算法在ID3算法的基础上做了改进，作者本来计划的是实现C4.5算法，考虑了一下还是从最基本的开始做起吧。
　　本文只做决策树学习算法入门使用，实现的ID3算法也是最基础的部分，并未考虑扩展的情况，因此对一些不规范 的数据并不能很好地处理。
　　如果发现了错误，欢迎指出。
　　查看本文源码