Java实现哈夫曼树及简易编码解码

一、基本概念

  首先了解哈夫曼树之前先要知道的知识点，这些也都是树（不是书）中的概念：

1、路径和路径长度

  在一棵树中，从一个结点往下可以达到的孩子或孙子结点之间的通路，称为路径。通路中分支的数目称为路径长度。若规定根结点的层数为1，则从根结点到第L层结点的路径长度为L-1。

2、结点的权及带权路径长度

  若将树中结点赋给一个有着某种含义的数值，则这个数值称为该结点的权。结点的带权路径长度为：从根结点到该结点之间的路径长度与该结点的权的乘积。

3、树的带权路径长度

  树的带权路径长度规定为所有叶子结点的带权路径长度之和，记为WPL。

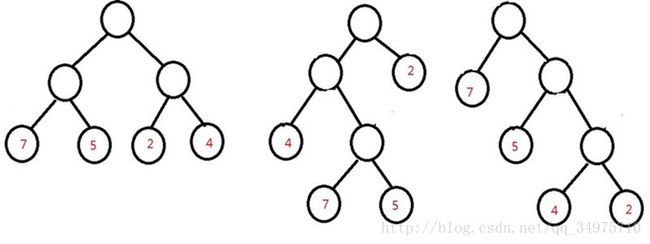
他们的带权长度分别为：
WPL1：7*2+5*2+2*2+4*2=36
WPL2：7*3+5*3+2*1+4*2=46
WPL3：7*1+5*2+2*3+4*3=35
第三棵树的带权路径长度最小。
给定n个带权值的叶子结点，若树的带权路径长度达到最小，称这样的二叉树为最优二叉树，也称为哈夫曼树(Huffman Tree)。

二、构建哈夫曼树

1. 将所有带权值的结点按权值从小到大排列；

2. 依次选取权值最小的结点放在树的底部，权值小的在左边(取出的结点相当于从这些结点的集合中剔除)；

3. 生成一个新节点作为这两个结点的父节点，且父节点的权值等于这两个结点权值之和，然后要把这个新结点放回我们需要构成树的结点中，继续进行排序；

4. 重复上述2、3步骤，直至全部节点形成一棵树，此树便是哈夫曼树，最后生成的结点即为根节点。这样构成的哈夫曼树，所有的存储有信息的结点都在叶子结点上。

例如：有四个结点 A、B、C、D，权值分别为2，3，1，5，构建哈夫曼树的过程如下

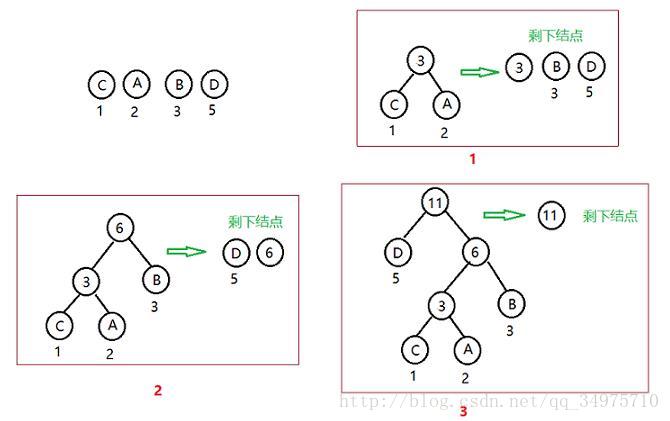
当第三次合并后就只剩下一个结点，此时这四个结点便构成了一个哈夫曼树，最后结点为树的根节点。

三、哈夫曼编码

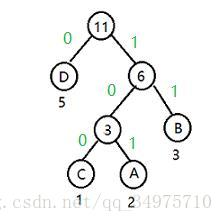
  从根节点出发，每个父节点都会有分支，现在给左右分支各赋予一个数值，做分支表示‘0’，有分支表示‘1’。当从根节点一直数到叶子结点过程中所经历的左右分支以‘0’、’1’表示时，每个叶子结点会形成一个特定的编码，这个就是哈夫曼编码，如上图中四个叶子结点的编码分别为：
A：101
B：11
C：100
D：0

  在电文传输中，需要将电文中出现的每个字符进行二进制编码。在设计编码时需要遵守两个原则：
（1）发送方传输的二进制编码，到接收方解码后必须具有唯一性，即解码结果与发送方发送的电文完全一样；
（2）发送的二进制编码尽可能地短。下面我们介绍两种编码的方式。

1 等长编码

  这种编码方式的特点是每个字符的编码长度相同（编码长度就是每个编码所含的二进制位数）。假设字符集只含有4个字符A，B，C，D，用二进制两位表示的编码分别为00，01，10，11。若现在有一段电文为：ABACCDA，则应发送二进制序列：00010010101100，总长度为14位。当接收方接收到这段电文后，将按两位一段进行译码。这种编码的特点是译码简单且具有唯一性，但编码长度并不是最短的。

2.不等长编码

  在传送电文时，为了使其二进制位数尽可能地少，可以将每个字符的编码设计为不等长的，使用频度较高的字符分配一个相对比较短的编码，使用频度较低的字符分配一个比较长的编码。例如，可以为A，B，C，D四个字符分别分配0，00，1，01，并可将上述电文用二进制序列：000011010发送，其长度只有9个二进制位，但随之带来了一个问题，接收方接到这段电文后无法进行译码，因为无法断定前面4个0是4个A，1个B、2个A，还是2个B，即译码不唯一，因此这种编码方法不可使用。
  因此，为了设计长短不等的编码，以便减少电文的总长，还必须考虑编码的唯一性，即在建立不等长编码时必须使任何一个字符的编码都不是另一个字符的前缀。
  这个问题可以采用哈夫曼编码解决。

四、构建哈夫曼树

将一个字符串中出现的字符生成其对应的哈夫曼编码，分为以下几步：
1. 统计出现的字符及频率
2. 将各个字符创建为叶子结点，频率为结点的权值，用链表保存这些叶子结点
3. 将结点队列中的结点按权值升序排列
4. 取出权值最小的两个结点构建父节点（要从链表中删除取出的结点），将新生成的父节点添加到结点链表，并从新排序
5. 重复4步骤，直到只剩下一个结点
6. 返回最后的结点，即为哈夫曼树的根节点。

结点类：

/**
 * 节点类
 * @author LiRui
 *
 */
public class HNode {

    public String code = "";// 节点的哈夫曼编码
    public String data = "";// 节点的数据
    public int count;// 节点的权值
    public HNode lChild;
    public HNode rChild;

    public HNode() {
    }

    public HNode(String data, int count) {
        this.data = data;
        this.count = count;
    }

    public HNode(int count, HNode lChild, HNode rChild) {
        this.count = count;
        this.lChild = lChild;
        this.rChild = rChild;
    }

    public HNode(String data, int count, HNode lChild, HNode rChild) {
        this.data = data;
        this.count = count;
        this.lChild = lChild;
        this.rChild = rChild;
    }

}

哈夫曼树类（为了省事都放在一个类里了，代码较长）：

/**
 * 哈夫曼树类
 * @author LiRui
 *
 */
public class Huffman {
    private String str;// 最初用于压缩的字符串    
    private HNode root;// 哈夫曼二叉树的根节点
    private boolean flag;// 最新的字符是否已经存在的标签
    private LinkedList charList;// 存储不同字符的队列 相同字符存在同一位置
    private LinkedList NodeList;// 存储节点的队列

     private class CharData {
         int num = 1; // 字符个数
         char c; // 字符

         public CharData(char ch){
             c = ch;
         }
     }

    /**
     * 构建哈夫曼树
     * 
     * @param str
     */
    public void creatHfmTree(String str) {
        this.str = str;

        NodeList = new LinkedList();
        charList = new LinkedList();

        // 1.统计字符串中字符以及字符的出现次数
        // 以CharData类来统计出现的字符和个数
        getCharNum(str);

        // 2.根据第一步的结构，创建节点
        creatNodes();

        // 3.对节点权值升序排序
        Sort(NodeList);

        // 4.取出权值最小的两个节点，生成一个新的父节点
        // 5.删除权值最小的两个节点，将父节点存放到列表中
        creatTree();

        // 6.重复第四五步，就是那个while循环
        // 7.将最后的一个节点赋给根节点
        root = NodeList.get(0);
    }

    /**
     * 统计出现的字符及其频率
     * 
     * @param str
     */
    private void getCharNum(String str) {

        for (int i = 0; i < str.length(); i++) {
            char ch = str.charAt(i); // 从给定的字符串中取出字符
            flag = true;

            for (int j = 0; j < charList.size(); j++) {
                CharData data = charList.get(j);

                if(ch == data.c){ 
                    // 字符对象链表中有相同字符则将个数加1
                    data.num++;
                    flag = false;
                    break;
                }
            }

            if(flag){
                // 字符对象链表中没有相同字符则创建新对象加如链表
                charList.add(new CharData(ch)); 
            }

        }

    }

    /**
     * 将出现的字符创建成单个的结点对象
     */
    private void creatNodes() {

        for (int i = 0; i < charList.size(); i++) {
            String data = charList.get(i).c + "";
            int count = charList.get(i).num;

            HNode node = new HNode(data, count); // 创建节点对象
            NodeList.add(node); // 加入到节点链表
        }

    }

    /**
     * 构建哈夫曼树
     */
    private void creatTree() {

        while (NodeList.size() > 1) {// 当节点数目大于一时
            // 4.取出权值最小的两个节点，生成一个新的父节点
            // 5.删除权值最小的两个节点，将父节点存放到列表中
            HNode left = NodeList.poll();
            HNode right = NodeList.poll();

            // 在构建哈夫曼树时设置各个结点的哈夫曼编码
            left.code = "0";
            right.code = "1";
            setCode(left);
            setCode(right);

            int parentWeight = left.count + right.count;// 父节点权值等于子节点权值之和
            HNode parent = new HNode(parentWeight, left, right);

            NodeList.addFirst(parent); // 将父节点置于首位
            Sort(NodeList); // 重新排序，避免新节点权值大于链表首个结点的权值
        }
    }

    /**
     * 升序排序
     * 
     * @param nodelist
     */
    private void Sort(LinkedList nodelist) {
        for (int i = 0; i < nodelist.size() - 1; i++) {
            for (int j = i + 1; j < nodelist.size(); j++) {
                HNode temp;
                if (nodelist.get(i).count > nodelist.get(j).count) {
                    temp = nodelist.get(i);
                    nodelist.set(i, nodelist.get(j));
                    nodelist.set(j, temp);
                }

            }
        }

    }

    /**
     * 设置结点的哈夫曼编码
     * @param root
     */
    private void setCode(HNode root) {

        if (root.lChild != null) {
            root.lChild.code = root.code + "0";
            setCode(root.lChild);
        }

        if (root.rChild != null) {
            root.rChild.code = root.code + "1";
            setCode(root.rChild);
        }
    }

    /**
     * 遍历
     * 
     * @param node
     *            节点
     */
    private void output(HNode node) {

        if (node.lChild == null && node.rChild == null) {
            System.out.println(node.data + ": " + node.code);
        }
        if (node.lChild != null) {
            output(node.lChild);
        }
        if (node.rChild != null) {
            output(node.rChild);
        }
    }

    /**
     * 输出结果字符的哈夫曼编码
     */
    public void output() {
        output(root);
    }



    /***********************以下是编解码的实现*************************/

    private String hfmCodeStr = "";// 哈夫曼编码连接成的字符串

    /**
     * 编码
     * @param str
     * @return
     */
    public String toHufmCode(String str) {

        for (int i = 0; i < str.length(); i++) {
            String c = str.charAt(i) + "";
            search(root, c);
        }

        return hfmCodeStr;
    }

    /**
     * 
     * @param root 哈夫曼树根节点
     * @param c 需要生成编码的字符
     */
    private void search(HNode root, String c) {
        if (root.lChild == null && root.rChild == null) {
            if (c.equals(root.data)) {
                hfmCodeStr += root.code; // 找到字符，将其哈夫曼编码拼接到最终返回二进制字符串的后面
            }
        }
        if (root.lChild != null) {
            search(root.lChild, c);
        }
        if (root.rChild != null) {
            search(root.rChild, c);
        }
    }


    // 保存解码的字符串
    String result="";
    boolean target = false; // 解码标记
    /**
     * 解码
     * @param codeStr
     * @return
     */
    public String CodeToString(String codeStr) {

        int start = 0;
        int end = 1;

        while(end <= codeStr.length()){
            target = false;
            String s = codeStr.substring(start, end);
            matchCode(root, s); // 解码
            // 每解码一个字符，start向后移
            if(target){
                start = end;
            }
            end++;
        }

        return result;
    }

    /**
     * 匹配字符哈夫曼编码，找到对应的字符
     * @param root 哈夫曼树根节点
     * @param code 需要解码的二进制字符串
     */
    private void matchCode(HNode root, String code){
        if (root.lChild == null && root.rChild == null) {
            if (code.equals(root.code)) {
                result += root.data; // 找到对应的字符，拼接到解码字符穿后
                target = true; // 标志置为true
            }
        }
        if (root.lChild != null) {
            matchCode(root.lChild, code);
        }
        if (root.rChild != null) {
            matchCode(root.rChild, code);
        }

    }
}

下面测试：

public static void main(String[] args) {

        Huffman huff = new Huffman();// 创建哈弗曼对象

        String data = readFile(); // 读取本地文件（自己写的方法，不想写可以自己随便定一个字符串）
        huff.creatHfmTree(data);// 构造树

        huff.output(); // 显示字符的哈夫曼编码

        // 将目标字符串利用生成好的哈夫曼编码生成对应的二进制编码
        String hufmCode = huff.toHufmCode(data); 
        System.out.println("编码:" + hufmCode);

        // 将上述二进制编码再翻译成字符串
        System.out.println("解码：" + huff.CodeToString(hufmCode));            
    }

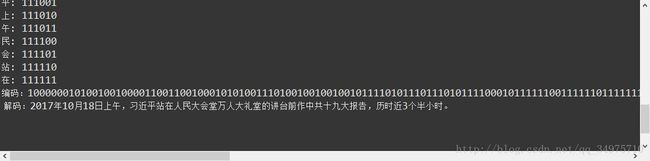
好了，大致过程解释这样子了（PS：这里的编解码只是做个演示，实际的没这么简单）。

---

生活不只是敲代码，如果你或你身边的人喜欢摄影或者生活的点点滴滴，可以关注下面的公众号~