hdu3685 Rotational Painting 求多边形重心和凸包

http://acm.hdu.edu.cn/showproblem.php?pid=3685

Rotational Painting

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 2614    Accepted Submission(s): 737

Problem Description

Josh Lyman is a gifted painter. One of his great works is a glass painting. He creates some well-designed lines on one side of a thick and polygonal glass, and renders it by some special dyes. The most fantastic thing is that it can generate different meaningful paintings by rotating the glass. This method of design is called “Rotational Painting (RP)” which is created by Josh himself. 

You are a fan of Josh and you bought this glass at the astronomical sum of money. Since the glass is thick enough to put erectly on the table, you want to know in total how many ways you can put it so that you can enjoy as many as possible different paintings hiding on the glass. We assume that material of the glass is uniformly distributed. If you can put it erectly and stably in any ways on the table, you can enjoy it. 

More specifically, if the polygonal glass is like the polygon in Figure 1, you have just two ways to put it on the table, since all the other ways are not stable. However, the glass like the polygon in Figure 2 has three ways to be appreciated. 

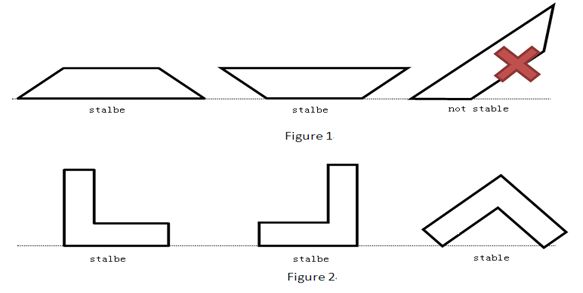
Pay attention to the cases in Figure 3. We consider that those glasses are not stable.

 

Input

The input file contains several test cases. The first line of the file contains an integer T representing the number of test cases. 

For each test case, the first line is an integer n representing the number of lines of the polygon. (3<=n<=50000). Then n lines follow. The ith line contains two real number x _i and y _i representing a point of the polygon. (x _i, y _i) to (x _i+1, y _i+1) represents a edge of the polygon (1<=in,y _n) to (x ₁, y ₁) also represents a edge of the polygon. The input data insures that the polygon is not self-crossed.

 

Output

For each test case, output a single integer number in a line representing the number of ways to put the polygonal glass stably on the table.

 

Sample Input

2 4 0 0 100 0 99 1 1 1 6 0 0 0 10 1 10 1 1 10 1 10 0

 

Sample Output

2 3

Hint

The sample test cases can be demonstrated by Figure 1 and Figure 2 in Description part.

 

Source

2010 Asia Hangzhou Regional Contest

题意：给一个多边形，问有几种稳定的摆放方式。。

思路：很简单。。。求出多边形的重心，然后由于不一定是凸多边形，所以再求下多边形凸包，枚举凸包的每一条边，看重心做垂足是否在边上，注意题目要求垂足在端点不算。。可以用点积看夹角是不是锐角来判断垂足位置。。

/**
 * @author neko01
 */
//#pragma comment(linker, "/STACK:102400000,102400000")
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include