二部图------KM算法、匈牙利算法

二分图的概念

二分图又称作二部图，是图论中的一种特殊模型。 
设G=(V, E)是一个无向图。如果顶点集V可分割为两个互不相交的子集X和Y，并且图中每条边连接的两个顶点一个在X中，另一个在Y中，则称图G为二分图。 

二分图的性质

定理：当且仅当无向图G的每一个回路的次数均是偶数时，G才是一个二分图。如果无回路，相当于任一回路的次数为0，故也视为二分图。

二分图匹配

给定一个二分图G，在G的一个子图M中，M的边集{E}中的任意两条边都不依附于同一个顶点，则称M是一个匹配。 
图中加粗的边是数量为2的匹配。 

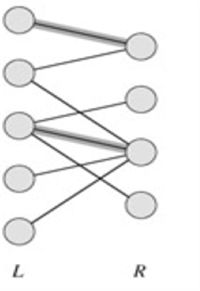
最大匹配

选择边数最大的子图称为图的最大匹配问题(maximal matching problem) 
如果一个匹配中，图中的每个顶点都和图中某条边相关联，则称此匹配为完全匹配，也称作完备匹配。 
图中所示为一个最大匹配，但不是完全匹配。 

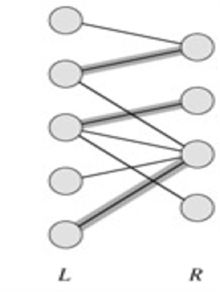
增广路径

增广路径的定义：设M为二分图G已匹配边的集合，若P是图G中一条连通两个未匹配顶点的路径（P的起点在X部，终点在Y部，反之亦可），并且属M的边和不属M的边(即已匹配和待匹配的边)在P上交替出现，则称P为相对于M的一条增广路径。 
增广路径是一条“交错轨”。也就是说, 它的第一条边是目前还没有参与匹配的,第二条边参与了匹配,第三条边没有..最后一条边没有参与匹配,并且起点和终点还没有被选择过，这样交错进行,显然P有奇数条边（为什么？）

寻找增广路径
 
红边为三条已经匹配的边。从X部一个未匹配的顶点x4开始，找一条路径： 
x4,y3,x2,y1,x1,y2x4,y3,x2,y1,x1,y2 
因为y2是Y部中未匹配的顶点，故所找路径是增广路径。 
其中有属于匹配M的边为{x2,y3},{x1,y1} 
不属于匹配的边为{x4,y3},{x2, y1}, {x1,y2} 
可以看出：不属于匹配的边要多一条！

 
如果从M中抽走{x2,y3},{x1,y1}，并加入{x4,y3},{x2, y1}, {x1,y2}，也就是将增广路所有的边进行”反色”,则可以得到四条边的匹配M’={{x3,y4}, {x4,y3},{x2, y1}, {x1,y2}} 
容易发现这样修改以后,匹配仍然是合法的,但是匹配数增加了一对。另外,单独的一条连接两个未匹配点的边显然也是交错轨.可以证明,当不能再找到增广轨时,就得到了一个最大匹配.这也就是匈牙利算法的思路. 
可知四条边的匹配是最大匹配

增广路径性质
由增广路的定义可以推出下述三个结论：

P的路径长度必定为奇数，第一条边和最后一条边都不属于M，因为两个端点分属两个集合，且未匹配。
P经过取反操作可以得到一个更大的匹配M’。
M为G的最大匹配当且仅当不存在相对于M的增广路径。
匈牙利算法
用增广路求最大匹配(称作匈牙利算法，匈牙利数学家Edmonds于1965年提出) 
算法轮廓：

置M为空
找出一条增广路径P，通过取反操作获得更大的匹配M’代替M
重复2操作直到找不出增广路径为止
找增广路径的算法
我们采用DFS的办法找一条增广路径： 
从X部一个未匹配的顶点u开始，找一个未访问的邻接点v（v一定是Y部顶点）。对于v，分两种情况：

如果v未匹配，则已经找到一条增广路
如果v已经匹配，则取出v的匹配顶点w(w一定是X部顶点)，边(w,v)目前是匹配的，根据“取反”的想法，要将(w,v)改为未匹配，(u,v)设为匹配，能实现这一点的条件是看从w为起点能否新找到一条增广路径P’。如果行，则u-v-P’就是一条以u为起点的增广路径。
匈牙利算法
cx[i]表示与X部i点匹配的Y部顶点编号 
cy[i]表示与Y部i点匹配的X部顶点编号

//伪代码
bool dfs(int u)//寻找从u出发的增广路径
{
    for each v∈u的邻接点
        if(v未访问){
            标记v已访问;
            if(v未匹配||dfs(cy[v])){
                cx[u]=v;
                cy[v]=u; 
                return true;//有从u出发的增广路径
            }
        }
    return false;//无法找到从u出发的增广路径
}
//代码
bool dfs(int u){
    for(int v=1;v<=m;v++)
        if(t[u][v]&&!vis[v]){
            vis[v]=1;
            if(cy[v]==-1||dfs(cy[v])){
                cx[u]=v;cy[v]=u;
                return 1;
            }
        }
    return 0;
}
void maxmatch()//匈牙利算法主函数
{
    int ans=0;
    memset(cx,0xff,sizeof cx);
    memset(cy,0xff,sizeof cy);
    for(int i=0;i<=nx;i++) 
        if(cx[i]==-1)//如果i未匹配
        { 
            memset(visit,false,sizeof(visit)) ; 
            ans += dfs(i); 
        }
    return ans ;
} 

 

一般对KM算法的描述，基本上可以概括成以下几个步骤： 
（1） 初始化可行标杆 
（2） 用匈牙利算法寻找完备匹配 
（3） 若未找到完备匹配则修改可行标杆 
（4） 重复（2）（3）直到找到相等子图的完备匹配 


KM算法是用于寻找带权二分图最佳匹配的算法。 

二分图：所有顶点可以分成两个集：X和Y，其中X和Y中的任意两个在同一个集中的点都不相连，而来自X集的顶点与来自Y集的顶点有连线。当这些连线被赋于一定的权重时，这样的二分图便是带权二分图。 

二分图匹配是指求出一组边，其中的顶点分别在两个集合中，且任意两条边都没有相同的顶点，这组边叫做二分图的匹配，而所能得到的最大的边的个数，叫做二分图的最大匹配。 

匈牙利算法

一般用于寻找二分图的最大匹配。算法根据一定的规则选择二分图的边加入匹配子图中，其基本模式为： 

初始化匹配子图为空 
While 找得到增广路径 
Do 把增广路径添加到匹配子图中 

增广路径有如下特性： 
1. 有奇数条边 
2. 起点在二分图的X边，终点在二分图的Y边 
3. 路径上的点一定是一个在X边，一个在Y边，交错出现。 
4. 整条路径上没有重复的点 
5. 起点和终点都是目前还没有配对的点，其他的点都已经出现在匹配子图中 
6. 路径上的所有第奇数条边都是目前还没有进入目前的匹配子图的边，而所有第偶数条边都已经进入目前的匹配子图。奇数边比偶数边多一条边 
7. 于是当我们把所有第奇数条边都加到匹配子图并把条偶数条边都删除，匹配数增加了1. 

例如下图，蓝色的是当前的匹配子图，目前只有边x0y0，然后通过x1找到了增广路径：x1y0->y0x0->x0y2 

 

其中第奇数第边x1y0和x0y2不在当前的匹配子图中，而第偶数条边x0y0在匹配子图中，通过添加x1y0和x0y2到匹配子图并删除x0y0，使得匹配数由1增加到了2。每找到一条增广路径，通过添加删除边，我们总是能使匹配数加1. 

增广路径有两种寻径方法，一个是深搜，一个是宽搜。

例如从x2出发寻找增广路径

深搜，x2找到y0匹配，但发现y0已经被x1匹配了，于是就深入到x1，去为x1找新的匹配节点，结果发现x1没有其他的匹配节点，于是匹配失败，x2接着找y1，发现y1可以匹配，于是就找到了新的增广路径。

宽搜，x2找到y0节点的时候，由于不能马上得到一个合法的匹配，于是将它做为候选项放入队列中，并接着找y1，于是匹配成功返回。相对来说，深搜要容易理解些，其栈可以由递归过程来维护，而宽搜则需要自己维护一个队列，并对一路过来的路线自己做标记，实现起来比较麻烦。 

对于带权重的二分图来说，我们可以把它看成一个所有X集合的顶点到所有Y集合的顶点均有边的二分图（把原来没有的边添加入二分图，权重为0即可），也就是说它必定存在完备匹配（即其匹配数为min(|X|,|Y|)）。为了使权重达到最大，我们实际上是通过贪心算法来选边，形成一个新的二分图（我们下面叫它二分子图好了），并在该二分图的基础上寻找最大匹配，当该最大匹配为完备匹配时，我们可以确定该匹配为最佳匹配。（在这里我们如此定义最大匹配：匹配边数最多的匹配和最佳匹配：匹配边的权重和最大的匹配。） 

贪心算法总是将最优的边优先加入二分子图，该最优的边将对当前的匹配子图带来最大的贡献，贡献的衡量是通过标杆来实现的。下面我们将通过一个实例来解释这个过程。 

有带权二分图： 

 
算法把权重转换成标杆，X集跟Y集的每个顶点各有一个标杆值，初始情况下权重全部放在X集上。由于每个顶点都将至少会有一个匹配点，贪心算法必然优先选择该顶点上权重最大的边（最理想的情况下，这些边正好没有交点，于是我们自然得到了最佳匹配）。最初的二分子图为：（可以看到初始化时X标杆为该顶点上的最大权重，而Y标杆为0） 

 
从X0找增广路径，找到X0Y4；从而从X1找不到增广路径--->必须往二分子图里边添加新的边，使得X1能找到它的匹配，同时使权重总和添加最大。由于X1通往Y4而Y4已经被X0匹配，所以有两种可能，①为X0找一个新的匹配点并把Y4让给X1，②为X1找一个新的匹配点，现在我们将要看到标杆的作用了。

根据传统的算法描述，能够进入二分子图的边的条件为L(x)+L(y)>=weight(xy)。当找不到增广路径时，对于搜索过的路径上的XY点，设该路径上的X顶点集为S，Y顶点集为T，对所有在S中的点xi及不在T中的点yj，计算d=min{(L(xi)+L(yj)-weight(xiyj))}，从S集中的X标杆中减去d，并将其加入到T集中的Y的标杆中，由于S集中的X标杆减少了，而不在T中的Y标杆不变，相当于这两个集合中的L(x)+L(y)变小了，也就是，有新的边可以加入二分子图了。从贪心选边的角度看，我们可以为X0选择新的边而抛弃原先的二分子图中的匹配边，也可以为X1选择新的边而抛弃原先的二分子图中的匹配边，因为我们不能同时选择X0Y4和X1Y4，因为这是一个不合法匹配，这个时候，d=min{(L(xi)+L(yj)-weight(xiyj))}的意义就在于，我们选择一条新的边，这条边将被加入匹配子图中使得匹配合法，选择这条边形成的匹配子图，将比原先的匹配子图加上这条非法边组成的非法匹配子图的权重和（如果它是合法的，它将是最大的）小最少，即权重最大了。好绕口的。用数学的方式表达，设原先的不合法匹配（它的权重最大，因为我们总是从权重最大的边找起的）的权重为W，新的合法匹配为W’，d为min{W-W’i}。在这个例子中，S={X0, X1}，Y={Y4}，求出最小值d=L(X1)+L(Y0)-weight(X1Y0)=2，得到新的二分子图： 

 
重新为X1寻找增广路径，找到X1Y0，可以看到新的匹配子图的权重为9+6=15，比原先的不合法的匹配的权重9+8=17正好少d=2。 
接下来从X2出发找不到增广路径，其走过的路径如蓝色的路线所示。形成的非法匹配子图：X0Y4，X1Y0及X2Y0的权重和为22。在这条路径上，只要为S={X0，X1，X2}中的任意一个顶点找到新的匹配，就可以解决这个问题，于是又开始求d。 
d=L(X0)+L(Y2)-weight(X0Y2)=L(X2)+L(Y1)-weight(X2Y1)=1. 
新的二分子图为： 

 

重新为X2寻找增广路径，如果我们使用的是深搜，会得到路径：X2Y0->Y0X1->X1Y4->Y4X0->X0Y2，即奇数条边而删除偶数条边，新的匹配子图中由这几个顶点得到的新的权重为21；如果使用的是宽搜，会得到路径X2Y1，另上原先的两条匹配边，权重为21。假设我们使用的是宽搜，得到的新的匹配子图为： 

 
接下来依次类推，直到为X4找到一个匹配点。 

KM算法的最大特点在于利用标杆和权重来生成一个二分子图，在该二分子图上面找最大匹配，而且，当些仅当找到完备匹配，才能得到最佳匹配。标杆和权重的作用在于限制新边的加入，使得加入的新边总是能为子图添加匹配数，同时又令权重和得到最大的提高。 

下面是匈牙利算法的dfs和bfs实现，是用c++实现的： 

Cpp代码 

//---------------------DFS---------------------------------  
#include  
#include  
using namespace std;  
  
#define MAXN 10  
int graph[MAXN][MAXN];  
int match[MAXN];  
int visitX[MAXN], visitY[MAXN];  
int nx, ny;  
  
bool findPath( int u )  
{  
    visitX[u] = 1;  
    for( int v=0; v  
#include  
using namespace std;  
  
#define MAXN 10  
int graph[MAXN][MAXN];  
//在bfs中，增广路径的搜索是一层一层展开的，所以必须通过prevX来记录上一层的顶点  
//chkY用于标记某个Y顶点是否被目前的X顶点访问尝试过。  
int matchX[MAXN], matchY[MAXN], prevX[MAXN], chkY[MAXN];  
int queue[MAXN];  
int nx, ny;  
  
int bfsHungarian()  
{  
    int res = 0;  
    int qs, qe;  
    memset( matchX, -1, sizeof(matchX) );  
    memset( matchY, -1, sizeof(matchY) );  
    memset( chkY, -1, sizeof(chkY) );  
  
    for( int i=0; i= 0 )  
                            prevX[matchY[v]] = u;  
                        else    //到达了增广路径的最后一站  
                        {  
                            flag = 1;  
                            int d=u, e=v;  
                            while( d!=-1 )  //一路通过prevX找到路径的起点  
                            {  
                                int t = matchX[d];  
                                matchX[d] = e;  
                                matchY[e] = d;  
                                d = prevX[d];  
                                e = t;  
                            }  
                        }  
                    }  
                }  
                qs++;  
            }  
            if( matchX[i] != -1 )  
                res++;  
        }  
    }  
    return res;  
}  

最优匹配算法因为是项目需要，我用的是java。 

Java代码 

public class KuhnMunkres {  
      
    private int maxN, n, lenX, lenY;  
    private double[][] weights;  
    private boolean[] visitX, visitY;  
    private double[] lx, ly;  
    private double[] slack;  
    private int[] match;  
      
    public KuhnMunkres( int maxN )  
    {  
        this.maxN = maxN;  
        visitX = new boolean[maxN];  
        visitY = new boolean[maxN];  
        lx = new double[maxN];  
        ly = new double[maxN];  
        slack = new double[maxN];  
        match = new int[maxN];  
    }  
      
    public int[][] getMaxBipartie( double weight[][], double[] result )  
    {  
        if( !preProcess(weight) )  
        {  
            result[0] = 0.0;  
            return null;  
        }  
        //initialize memo data for class  
        //initialize label X and Y  
        Arrays.fill(ly, 0);  
        Arrays.fill(lx, 0);  
        for( int i=0; i= 0 )  
                result[0] += weights[match[i]][i];  
        }  
        return matchResult();  
    }  
      
    public int[][] matchResult()  
    {  
        int len = Math.min(lenX, lenY);  
        int[][] res = new int[len][2];  
        int count=0;  
        for( int i=0; i=0 && match[i]maxN || lenY>maxN )  
            return false;  
        Arrays.fill(match, -1);  
        n = Math.max(lenX, lenY);  
        weights = new double[n][n];  
        for( int i=0; i