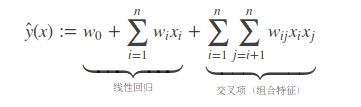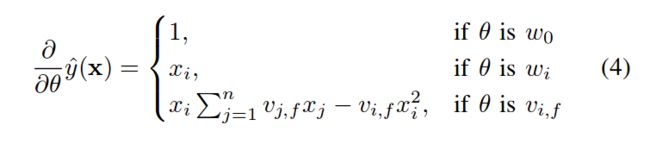传统推荐算法(四) 手把手教你用tensorflow实现FM算法

1.FM背景与简介

FM主要是为了解决稀疏数据下的特征组合问题。2010年，日本大阪大学(Osaka University)的 Steffen Rendle 在矩阵分解(MF)、SVD++[2]、PITF[3]、FPMC[4] 等基础之上，归纳出针对高维稀疏数据的因子机(Factorization Machine, FM)模型[13]。因子机模型可以将上述模型全部纳入一个统一的框架进行分析[1]。目前，FM被广泛的应用于广告预估模型中，相比LR而言，效果强了不少。

1.1 稀疏数据

高维的稀疏矩阵是工程中常见的问题，比如下图：

图中每一个样本对应多个属性，分别是User,Movie,Other Movies rated,Time,Last Movie rated，由于这些属性都是categorical类型，所以一般进行One-hot编码转换为数值类型，但是由于每个属性都有多个离散的取值，所以One-hot编码之后样本空间相比原来变大了许多，而特征矩阵也会变得非常稀疏。假设有10000部电影，有10000个用户，单看前两条，每个样本的二阶交叉特征维度就是一亿维，但是每个特征中只有两维取值不为0，非常稀疏。在CTR/CVR预测时，One-Hot编码常会导致样本的稀疏性，样本的稀疏性是实际问题中不可避免的挑战。

同时通过观察大量的样本数据可以发现，某些特征经过关联之后，与label之间的相关性就会提高。如：“USA”与“Thanksgiving”、“China”与“Chinese New Year”这样的关联特征，对用户的点击有着正向的影响。换句话说，来自“China”的用户很可能会在“Chinese New Year”有大量的浏览、购买行为，而在“Thanksgiving”却不会有特别的消费行为。这种关联特征与label的正向相关性在实际问题中是普遍存在的，如“化妆品”类商品与“女”性，“球类运动配件”的商品与“男”性，“电影票”的商品与“电影”品类偏好等。[5]。

显然，不同特征之间是有关联的，表示特征之间的关联，一种直接的方法是构建组合特征[5]。那么怎么组合特征呢？

1.2 FM模型

SVM就曾通过多项式核函数来实现特征的交叉。实际上，多项式是构建组合特征的一种非常直观的模型。我们先看一下二阶多项式的建模：

外层求和i实际上只取到了n-1，显然组合特征有n(n-1)/2个，如果特征有万级别，那么参数就有亿级别，这种计算量是很大的。

而且在稀疏性普遍存在的应用场景种，二次项参数的训练非常困难。以为每一个wij在训练时都要要求xi,xj不为零，否则梯度下降时梯度恒为零，而实际上xi,xj同时非零的情况非常少见，这会导致大部分参数无法学习，模型的性能也可想而知。那么如何解决二次项参数的训练问题呢？

矩阵分解提供了思路，矩阵分解吧rating矩阵分为user矩阵和item矩阵的乘积来进行低秩近似，这里FM引入辅助向量V来表示W:

这样有什么好处呢？[6]中的解释我觉得非常好：

2.FM模型求解

目前FM模型的求解方法主要有以下三种[12]：
随机梯度下降法（Stochastic Gradient Descent, SGD）
交替最小二乘法（Alternating Least Square Method，ALS）
马尔科夫链蒙特卡罗法（Markov Chain Monte Carlo，MCMC）

FM论文里给出了SGD求解方法，这了直接把论文里的求解粘贴过来，然后步步解读：

第一步到第二步根据这个公式理解：

这样理解起来不太直观，可以把第一步的式子看成是对矩阵上三角元素的求和，结果就是二分之一矩阵所有元素减去对角线元素的和。

第二步到第三部是直接展开。第三步到第四步我写了个详细的过程：

其实就是利用了多重求和的一个基本公式：

引入辅助向量V之前，计算复杂度为O(n²)，引入V之后，为O(kn²)，而通过2.1中的交叉项求解，我们知道，计算复杂度为O(kn)。一般来说k远小于n，我们可以FM可以在线性时间对新样本进行预测。

之后就可以用梯度下降法求解了，FM模型的梯度为：

3. FM优缺点分析

跑完了代码，有兴趣再来看看优缺点吧。

优点

1)FM模型可以在非常稀疏的数据中进行参数估计；
2)FM模型拥有线性的时间复杂度，可以在亿级别的大数据；
3)FM模型是一个通用模型，可以用在任何特征值为实值的情况下;
4)FM模型可以将上千万维的特征压缩为几百维甚至几十维，极大地减少了模型的参数，参数大大减少，模型的泛化能力也大大增强。

缺点

引用下知乎用户“屈伟”的说法[11]：

4.期待已久的tensorflow实战

数据处理

首先来看数据处理函数：

def vectorize_dic(dic, ix=None, p=None):
    if(ix == None):
        d = count(0)
        ix = defaultdict(lambda:next(d))
        
    n = len(list(dic.values())[0])
    g = len(list(dic.keys()))
    nz = n*g
    
    col_ix = np.empty(nz, dtype=int)
    
    i = 0
    for k, lis in dic.items():
        col_ix[i::g] = [ix[str(k)+str(el)] for el in lis]
        i += 1
    
    row_ix = np.repeat(np.arange(n), g)
    data = np.ones(nz);print('data.shape ', data.shape)

    if(p == None):
        p = len(ix)
        
    ixx = np.where(col_ix < p)
    
    return csr.csr_matrix(
        (data[ixx], (row_ix[ixx], col_ix[ixx])), shape=(n, p)), ix

这份代码里最难理解的就是这个函数，因为里面的小知识点较多。但是我们把握核心就行了，就是这个csr.csr_matrix。由于数据过于稀疏，只需要存储有用的信息(非零值)即可。csr_matrix提供了两种不错的表示方法。

第一种：

csr_matrix((data, (row_ind, col_ind)), [shape=(M, N)])

其中row_ind和col_ind代表data中数据所在的行和列，就这么简单。这个也是程序中用到的方法。
第二种：

csr_matrix((data, indices, indptr), [shape=(M, N)])

indicies代表列，indptr的长度为行数加1，其中的第i个元素代表前i-1行中的data数据个数，那么第n+1个元素就是是len(data)，即data中的所有数据。我们根据indptr可以确定data中每个元素所在的行数，根据indices确定每个元素的列数，那么矩阵就可以唯一确定了。这种表示方法推荐看[10]中的解读。

了解csr_matrix之后，我们就要关注row_ind和col_ix了。样本数为n，属性数为g，那么row_ind表示为(0,0,…0,1,1,…1,…,n-1,n-1,…,n-1)也就不难理解，每g个元素表示一个样本的行。那么col_ix也就很明显了，就是样本的各属性取值再one-hot编码向量中的位置。

这个函数我推荐大家把每个变量打印出来看看，就知道是什么意思了。博主在原来代码的基础上，加了一些调试代码(就是打印出关键变量)方便大家理解代码。觉得这个函数不好理解的可以试试。

静态图定义

首先看一下各种变量定义：

n, p = x_train.shape
# number of latent factors
k = 10
# design features of users
X = tf.placeholder('float', shape=[None, p])
# target vector
Y = tf.placeholder('float', shape=[None, 1])

# bias and weights
w0 = tf.Variable(tf.zeros([1]))
W = tf.Variable(tf.zeros([p]))

# matrix factorization factors, randomly initialized
V = tf.Variable(tf.random_normal([k, p], stddev=0.01))

# estimation of y, initialized to 0
Y_hat = tf.Variable(tf.zeros([n, 1]))

W这里的定义可以当成行向量来理解，看看Y_hat就知道列向量怎么定义了。

然后定义损失函数和优化器：

# calculate output with FM equation
linear_terms = tf.add(w0, tf.reduce_sum(tf.multiply(W, X), 1, keepdims=True))
pair_interactions = tf.multiply(0.5, 
                                tf.reduce_sum(
                                    tf.subtract(
                                        tf.pow(tf.matmul(X,tf.transpose(V)), 2), 
                                        tf.matmul(tf.pow(X, 2), tf.pow(tf.transpose(V), 2))), 
                                    1, keepdims=True))
Y_hat = tf.add(linear_terms, pair_interactions)
lambda_w = tf.constant(0.001, name='lambda_w')
lambda_v = tf.constant(0.001, name='lambda_v')
l2_norm = tf.reduce_sum(tf.multiply(lambda_w, tf.pow(W,2)))+tf.reduce_sum(tf.multiply(lambda_v, tf.pow(V,2)))
error = tf.reduce_mean(tf.square(tf.subtract(Y, Y_hat)))
loss =  tf.add(error, l2_norm)

optimizer = tf.train.GradientDescentOptimizer(learning_rate=0.01).minimize(loss)

原作者对l2_norm的处理我觉得有些问题，做了些改进。问题不大。

这里对矩阵的处理推荐大家看着代码自己尝试一下，不然下次自己可能写不出来。关键是要时刻注意各种变量的shape。

训练和测试

# In[77]: train process
epoches = 2
batch_size = 100

init = tf.global_variables_initializer()
sess = tf.Session()

sess.run(init)

for epoch in tqdm(range(epoches), unit='epoch'):
    perm = np.random.permutation(x_train.shape[0])
    for bx, by in batcher(x_train[perm], y_train[perm], batch_size):
        sess.run(optimizer, feed_dict={
            X:bx.reshape(-1, p),
            Y:by.reshape(-1, 1)
        })


# In[81]: test process


errors = []
for bx, by in batcher(x_test, y_test):
    errors.append(sess.run(error, feed_dict={
        X:bx.reshape(-1, p),
        Y:by.reshape(-1, 1)
    }))
RMSE = np.sqrt(np.array(errors).mean())
print(RMSE)

sess.close()

这里使用tqdm可以再jupyter notebook上实时显示训练进度。

本文参考python2代码：
https://github.com/babakx/fm_tensorflow/blob/master/fm_tensorflow.ipynb

完整代码网址：
https://github.com/wyl6/Recommender-Systems-Samples/tree/master/RecSys%20Traditional/MF/FM

参考

[1] https://tracholar.github.io/machine-learning/2017/03/10/factorization-machine.html

[2] S. Rendle and L. Schmidt-Thieme, “Pairwise interaction tensor factorization for personalized tag recommendation,” in WSDM ’10: Proceedings of the third ACM international conference on Web search and data mining. New York, NY, USA: ACM, 2010, pp. 81–90.

[3] S. Rendle, C. Freudenthaler, and L. Schmidt-Thieme, “Factorizing personalized markov chains for next-basket recommendation,” in WWW ’10: Proceedings of the 19th international conference on World wide web. New York, NY, USA: ACM, 2010, pp. 811–820.

[4]: A two-stage ensemble of diverse models for advertisement ranking in KDD Cup 2012[C]//KDDCup. 2012.

[5] https://plushunter.github.io/2017/07/13/%E6%9C%BA%E5%99%A8%E5%AD%A6%E4%B9%A0%E7%AE%97%E6%B3%95%E7%B3%BB%E5%88%97%EF%BC%8826%EF%BC%89%EF%BC%9A%E5%9B%A0%E5%AD%90%E5%88%86%E8%A7%A3%E6%9C%BA%EF%BC%88FM%EF%BC%89%E4%B8%8E%E5%9C%BA%E6%84%9F%E7%9F%A5%E5%88%86%E8%A7%A3%E6%9C%BA%EF%BC%88FFM%EF%BC%89/

[6] https://zhuanlan.zhihu.com/p/37963267

[7] https://zhuanlan.zhihu.com/p/35753471

[8] https://docs.scipy.org/doc/scipy/reference/generated/scipy.sparse.csr_matrix.html

[9] https://blog.csdn.net/u012871493/article/details/51593451

[10] https://blog.csdn.net/u012871493/article/details/51593451

[11] https://www.zhihu.com/question/62109451

[12] https://zhuanlan.zhihu.com/p/61096338

[13] Rendle, S. (2010, December). Factorization machines. In 2010 IEEE International Conference on Data Mining (pp. 995-1000). IEEE.

公众号

更多精彩内容请移步公众号:推荐算法工程师

感觉公众号内容不错点个关注呗