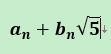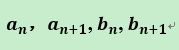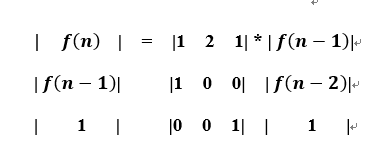一类常见的矩阵快速幂题型 总结
Googlecode jam 2008 Round 1A(c.Numbers)
【题意】计算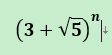
的小数点前三位数，不足三位补0,正整数n的最大值为20亿。
【前提】：满足
的值在【0，1】范围
首先将
展开之后可以发现
的形式，同样的，有
因此，
是个整数，
其中
这正是解题的关键！
由于
所以的整数部分等于
根据以上的推导
只要高效的求出an就可以解决这个问题了
由于
为观察仔细，进一步展开得：
得出
的递推关系
因此，可以用矩阵表示这个递推关系，使用矩阵快速幂，在O（logn）的时间里求出和,由于此题只要取前3位，因此对1000取模就可以了
代码：
#include
#include
#include
#include
using namespace std;
typedef long long LL;
const LL siz=2; // max size of the matrix,
#define MODD(a,b) (((a%b)+b)%b)
LL A,B,N,M,ret;
struct mut{
LL mat[siz][siz];
mut(){
memset(mat,0,sizeof(mat));
}
void init(LL a,LL b,LL c,LL d){
mat[0][0]=a;
mat[0][1]=b;
mat[1][0]=c;
mat[1][1]=d;
}
mut operator *(const mut &c){
mut res;
for(int i=0; i>=1;
AC=AC*AC;
}
return ans;
}
int main()
{
int t;
scanf("%d",&t);
while(t--){
scanf("%lld",&N);
M=1000;
AC.init(3,5,1,3);
mut ans=poww(N);
printf("%03lld\n",MODD(2*ans.mat[0][0]-1,M));
}
return 0;
} HDU 2256 Problem of Precision
【题意】：
【思路】和上题思路一样：
代码：
/*
* Problem: HDU No.2256
* Running time: 15MS
* Complier: G++
* Author: javaherongwei
* Create Time: 23:56 2015/9/21 星期一
*/
#include
#include
#include
#include
using namespace std;
typedef long long LL;
const LL siz=2; // max size of the matrix,
#define MODD(a,b) (((a%b)+b)%b)
LL A,B,N,M,ret;
struct mut{
LL mat[siz][siz];
mut(){
memset(mat,0,sizeof(mat));
}
void init(LL a,LL b,LL c,LL d){
mat[0][0]=a;
mat[0][1]=b;
mat[1][0]=c;
mat[1][1]=d;
}
mut operator *(const mut &c){
mut res;
for(int i=0; i>=1;
AC=AC*AC;
}
return ans;
}
int main(){
int t;
scanf("%d",&t);
while(t--){
scanf("%lld",&N);
M=1024;
AC.init(5,12,2,5);
mut ans=poww(N);
printf("%lld\n",MODD(2*ans.mat[0][0]-1,M));
}
return 0;
} HDU 1575 Tr A
【题目链接】：click here~~
24K纯裸的矩阵计算：
【题意】：给定一个n*n的矩阵要求矩阵的k次幂之后的矩阵的对角线的和
代码：
/*
* Problem: HDU No.1575
* Running time: 0MS
* Complier: G++
* Author: javaherongwei
* Create Time: 8:10 2015/9/22 星期二
*/
#include
#include
#include
#include
using namespace std;
typedef long long LL;
#define MODD(a,b) (((a%b)+b)%b)
LL A,B,K,M,ret;
LL N;
LL siz; // max size of the matrix,
struct mut{
LL mat[10][10];
mut(){
memset(mat,0,sizeof(mat));
}
void init(){
for(int i=0; i>=1;
AC=AC*AC;
}
return ans;
}
int main(){
int t;scanf("%d",&t);
while(t--){
scanf("%d %lld",&N,&K);M=9973;siz=N;
for(int i=0; i CodeForces 185A Plant
【题目链接】
点击打开cf 185A
【思路】: 递推+矩阵快速幂
分析:
1 题目要求找到在n年后向上三角形的个数
2 写出前面的几个数F(0) = 1 , F(1) = 3 , F(2) = 10 , F(3) = 36 ，我们可以发现每一个向上三角形在后面形成的时候必然是分成了3个向上+1个向下的，总共分成了4个，这是包含了向下的，所以要减去，然后发现F(1向下)=1，F(2想下)=3-1=2，因此向下的可以推出关系：
从而找到通项公式 ：
构造矩阵：
之后就是矩阵快速幂了
代码：
/*
* Problem: CodeForces 185A
* Running time: 8MS
* Complier: G++
* Author: javaherongwei
* Create Time: 9:10 2015/9/22 星期二
*/
#include
#include
#include
#include
using namespace std;
typedef long long LL;
#define MODD(a,b) (((a%b)+b)%b)
LL A,B,K,M,ret;
LL N;
const int siz=2; // max size of the matrix,
struct mut{
LL mat[siz][siz];
mut(){
memset(mat,0,sizeof(mat));
}
void init(LL a,LL b,LL c,LL d){
mat[0][0]=a;mat[0][1]=b;
mat[1][0]=c;mat[1][1]=d;
}
mut operator *(const mut &c){
mut res;
for(int i=0; i>=1;
AC=AC*AC;
}
return ans;
}
int main(){
//int t;scanf("%d",&t);
// while(t--){
while(~scanf("%lld",&N)){
M=1e9+7;
AC.init(4,-1,0,2);
mut ans=poww(N);
printf("%lld\n",MODD(ans.mat[0][0]*1+ans.mat[0][1]*1,M));
}
return 0;
} HDU 2842 Chinese Rings
【题目链接】点击打开hdu2842
【思路】: 矩阵快速幂
【分析】:
1 题目的意思是给定n个环，和一些规则：
If the first k rings are all off and the (k + 1)th ring is on, then the (k + 2)th ring can be taken off or taken on with one step. (0 ≤ k ≤ 7)
要把所有的环全部拆下最少需要的步数
2 题目规定如果要拆第n个环，那么第n-1个要挂着，n-2环要被拆下。那么我们设f(n)表示拆下前n个环的最少的步骤
那么考虑第n个环的情况，第n-1个环必须要挂着，n-2环要拆下，那么这一步就要f(n-2)，拆下第n个需要1步。然后只剩下第n-1个环，由于n-1环需要第n-2环挂着，所以我们需要把前n-2个环挂上去，所以需要f(n-2)，剩下n-1个需要拆下需要f(n-1)。那么总的需要:
3 接下来利用矩阵快速幂即可
代码：
/*
* Problem: HDU 2842
* Running time: 0MS
* Complier: G++
* Author: javaherongwei
* Create Time: 9:10 2015/9/22 星期二
*/
#include
#include
#include
#include
using namespace std;
typedef long long LL;
#define MODD(a,b) (((a%b)+b)%b)
LL A,B,K,M,ret;
LL N;
const int siz=3; // max size of the matrix,
struct mut{
LL mat[siz][siz];
mut(){
memset(mat,0,sizeof(mat));
}
void init(LL a1,LL a2,LL a3,LL b1,LL b2,LL b3,LL c1,LL c2,LL c3){
mat[0][0]=a1;mat[0][1]=a2;mat[0][2]=a3;
mat[1][0]=b1;mat[1][1]=b2;mat[1][2]=b3;
mat[2][0]=c1;mat[2][1]=c2;mat[2][2]=c3;
}
mut operator *(const mut &c){
mut res;
for(int i=0; i>=1;
AC=AC*AC;
}
return ans;
}
int main(){
//int t;scanf("%d",&t);
// while(t--){
while(~scanf("%lld",&N),N){
if(N==1){
puts("1");
continue;
}
M=200907;
AC.init(1,2,1,1,0,0,0,0,1);
mut ans=poww(N-2);
printf("%lld\n",MODD(ans.mat[0][0]*2+ans.mat[0][1]*1+ans.mat[0][2]*1,M));
}
return 0;
}