双向循环链表的插入排序
前两篇博文,我讨论了链表的冒泡排序和选择排序(以Linux内核链表为例),这篇文章,我想说说插入排序。
一、复习数组的插入排序
插入排序在算法思想中属于“减治法”。
减治法的基本思想是:规模为n的原问题的解与较小规模的子问题的解之间具有某种关系。由于存在这种关系,所以只需求解其中一个较小规模的子问题就可以得到原问题的解。
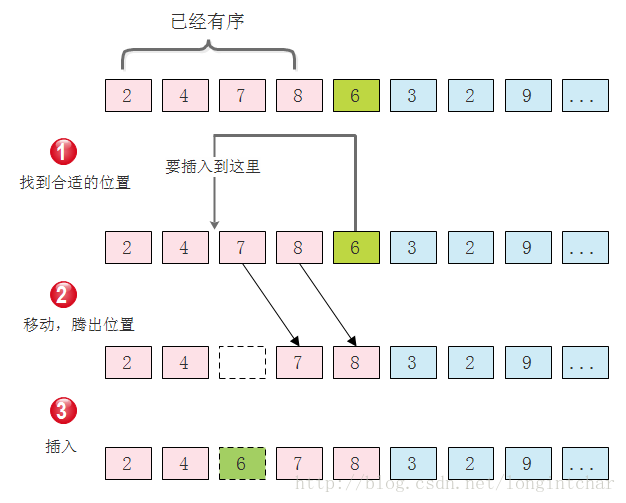
插入排序就是基于“减治法”中的“减一技术”实现的。如果题目要求对a[0]到a[n-1]进行排序,我幻想从a[0]到a[n-2]已经是有序的了,那么我需要做的就是在这些有序的元素中为a[n-1]找到一个合适的位置,然后把它插到那里就行。
虽然插入排序基于递归思想,可从顶至下实现;但是,从底至上地实现这个算法——使用迭代会效率更高。从a[1]开始,到a[n-1]为止,a[i]被插入到数组的前i个有序元素中的适当位置上(但是,和选择排序不同,这个位置一般来说并不是它的最终位置)。
示意图如下:
二、内核链表的插入排序
完整代码如下。(list.h文件这里就不列了,有需要的话可以参考我的博文http://blog.csdn.net/longintchar/article/details/78034827)
#include 以上代码运行结果如下:
6 4 7 9 2 8 5 1 3 7
1 2 3 4 5 6 7 7 8 9
三、代码解析
1. swap函数
可以参考我的博文http://blog.csdn.net/longintchar/article/details/78638975
2. list_for_each_from宏
#define list_for_each_from(cur, head) \
for (; cur != head; cur = (cur)->next)这个宏表示从当前结点开始遍历,一直到链表尾端。
3. list_for_each_reverse_continue宏
#define list_for_each_reverse_continue(cur, head) \
for (cur = (cur)->prev; cur != (head); cur = (cur)->prev)这个宏表示从当前结点的前一个结点开始,逆序遍历,一直到第一个结点。
4. __list_add函数
static inline void __list_add(struct list_head *new,
struct list_head *prev,
struct list_head *next)
{
next->prev = new;
new->next = next;
new->prev = prev;
prev->next = new;
} 把new指向的结点插入到prev和next结点之间。
5. insert_sort函数
void insert_sort(struct list_head *head,
int(*cmp)(struct list_head *a,
struct list_head *b))
{
struct list_head *i, *j,*temp;
i = head->next->next; //i指向第2个结点
list_for_each_from(i,head){ //i从第2个结点开始遍历,因为第1个已经有序
j = i->prev; //j指向i的前一个结点
if (cmp(j, i) <= 0) //从表头开始,按照升序排列
continue;
list_for_each_reverse_continue(j,head){
if(cmp(j,i) <= 0)
break;
}
temp = i->next; //因为下文要删除i结点,所以记录i结点的下一个结点
list_del(i);
__list_add(i,j,j->next); //把i插入到j的后面
i = temp->prev; //i指针归位
}
}6~7行:i从第二个结点开始,一直遍历到最后一个结点;
第10行:j指向i结点的前驱,如果j结点小于等于i结点,说明i不需要插入,它已经在合适的位置(不一定是最终位置)上了,此时进入下一轮迭代;
第12~14行:能执行到第12行,说明j结点大于i结点,这时候我们要做的是——从j向前找,找到第一个小于等于i的结点,这个结点用j指示。找到后跳出这层循环。
17~18行:我们需要把i结点插入到j的后面。
16和19行:因为i结点移动了,所以i指针需要归位,第16行记录了i结点的下一个结点,叫temp,第19行让i指向temp的前驱,完成归位。为什么要归位?可以参考我的博文 http://blog.csdn.net/longintchar/article/details/78638975 中的4.4节。
【完】