1:快速排序
快速排序的最坏情况时间复杂度为Θ(n^2)。虽然最坏情况时间复杂度很差,但是快速排序通常是实际排序应用中最好的选择,因为它的平均性能很好。它的期望运行时间复杂度为Θ(n lg n),而且Θ(n lg n)中蕴含的常数因子非常小,而且它还是原址排序的。
2:基本思想
快速排序采用分治法进行排序,首先在数组中选择一个元素P,根据元素P将数组划分为两个子数组,在元素P左侧的子数组的所有元素都小于或等于该元素P,右侧的子数组的所有元素都大于元素P。
下面是对一个典型子数组A[p...r]排序的分治过程的三个步骤:
a、分解:数组A[p..r]被划分为两个子数组A[p..q-1]和A[q+1..r]使得A[p..q-1]中的每个元素都小于等于A(q),而且,元素A(q)小于等于A[q+1..r]中的元素。下标q也在这个划分过程中进行计算。
b、解决:通过递归调用快速排序,对子数组A[p..q-1]和A[q+1...r]排序。
c、合并:快速排序对子数组采用就地排序,将两个子数组的合并并不需要操作。
该算法的伪代码如下:
QUICKSORT( A, p, r )
if p < r
then q =PARTITION( A, p, r );
QUICKSORT( A,p, q - 1);
QUCKSORT( A, q+ 1, r );
该算法的关键部分就是PARTITION,PARTITION不仅将数组分为两个子数组,而且返回选择key元素的位置。
partition子程序的伪代码如下,该过程的时间复杂度为Θ(n):
PARTITION( A, p, r )
x = A[r]; //选取最后一个元素为比较值(主元,pivot element)
i = p - 1; //i是分界点,i之前(包括i)的元素都小于x,i之后,j之前的元素都大于x
for( j = p; j <= r - 1;j ++ )
if ( A[j] <= x )
{
i ++;
exchange(A[i], A[j] );
}
exchange( A[i+1] ,A[r] );
return i + 1;
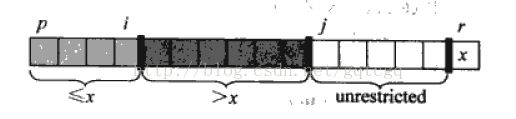
在PARTITION中,首先选择一个主元,根据该主元对数组进行划分,划分为4部分,如下图所示:
对照代码中的部分,这4部分包括:
a:范围pki中, A[k]x;
b:范围i+1kj-1中,A[k];
c:范围jkr-1中,数组元素未划分,最终都要划分到上面俩范围之一;
d:k=r,则A[k]x;
3:快速排序的性能
快速排序的运行时间依赖于划分是否平衡,如果划分平衡,那么快速排序算法性能与归并排序一样,如果划分不平衡,那么快速排序的性能就接近于插入排序了。
最坏情况下,每次划分的两个子问题都分别包含了n-1个元素和0个元素。划分的时间代价为O(n),因为对一个大小为0的数组进行递归调用后,返回了T(n)=O(1),故算法的运行时间可递归的表示为:
T(n) = T(n-1) + T(0) + O(n)= T(n-1) + O(n)
该递归式的解为:T(n) =Θ(n^2)。因此,最坏情况下,也就是数组中元素已经排好序的时候,快速排序的时间复杂度为Θ(n^2),而在同样的情况下,插入排序的时间复杂度为O(n)。
最好的情况,每次划分都是平均的划分为n/2个元素子数组,此时递归式为:T(n) = 2T(n/2) + O(n)
该递归式可得T(n) = O(nlgn)。
快速排序的平均运行时间更接近于其最好情况,而非最坏情况,事实上,任何一种常数比例的划分都会产生深度为Θ(nlg n)的递归树,其中每一层的代价都是O(n),因此,只要划分是常数比例的,算法的运行时间总是O(n lgn)。
4:快速排序的随机化版本
当输入的数据是随机排列的时候,快速排序的时间复杂度是O(n lgn)。但是在实际中,输入并不总是随机的,因此需要在算法中引入随机性,可以对输入进行重新排列是算法实现随机化, 也可以进行随机抽样,随机抽样是从数组A[p…r]中随机选择一个元素作为主元,算法如下:
RANDOMIZED-PARTITION(A, p, r)
I = RANDOM(p,r)
exchange A[r] with A[i]
return PARTITION(A, p, r)
RANDOMIZED-QUICKSORT(A, p, r)
if p < r
q = RANDOMIZED -PARTITION(A, p, r );
QUICKSORT( A, p, q -1);
QUCKSORT( A, q + 1, r);
5:尾递归
普通的快速排序需要两次的递归调用,分别针对左子数组和右子数组,可以使用尾递归技术消除QUICKSORT中第二个递归调用,也就是用循环代替它,好的编译器都具有这种功能:
TAIL-RECURSIVE-QUICKSORT(A, p, r)
while p < r
q = PARTITION(A, p, r)
TAIL-RECURSIVE-QUICKSORT(A,p, q-1)
p = q+1
6:完整代码如下:
int partition(int *set, int begin, int end)
{
int i, j, k;
int x;
x = set[end];
i = begin - 1;
for(j = begin; j <= end - 1; j++)
{
if(set[j] <= x)
{
i++;
exchange(set+i, set+j);
}
}
exchange(set+i+1, set+end);
return i+1;
}
void quicksort(int *set, int begin, int end)
{
int index;
if(begin < end)
{
index = partition(set, begin, end);
quicksort(set, begin, index-1);
quicksort(set, index+1, end);
}
}