前言
最近遇到一个问题,需要在以一个坐标为中心的区域内生成一组均匀分布的随机点,首先想到的就是以圆作为区域。
圆内随机点
方法1:
根据\(x^{2}+y^{2}=R^{2}\),那么自让想到可以先随机生成[-R,R]间的横坐标x,然后生成[\(-\sqrt{R^{2}-X^{2}},\sqrt{R^{2}-X^{2}}\)]范围内的随机数y,那么(x,y)自然也就是在圆内的随机点了。
写一段代码看一看:
def random_point_in_circle(point_num, radius):
for i in range(2,point_num+1):
x=random.uniform(-radius,radius)
y_max=math.sqrt(radius*radius-x*x)
y=random.uniform(-y_max,y_max)
plt.plot(x,y,'*',color="blue")
def main():
pi = np.pi
theta = np.linspace(0, pi * 2, 1000)
R = 1
x = np.sin(theta) * R
y = np.cos(theta) * R
plt.figure(figsize=(6, 6))
plt.plot(x, y, label="cycle", color="green", linewidth=2)
plt.title("random_points_in_circle")
random_point_in_circle(4000, R)
plt.legend()
plt.show()
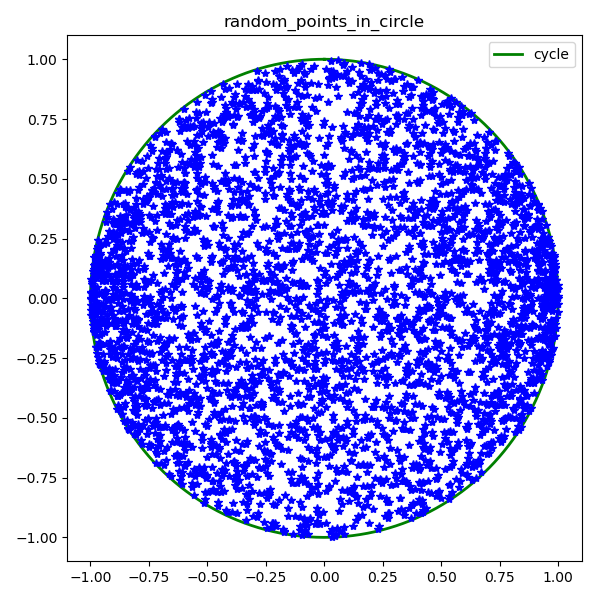
if __name__=="__main__":
main()看到这个图应该立刻就知道哪里出错了,当x越靠近圆的边缘的话,y的范围就会越小,所以两边边缘的点会非常密集,不能算"均匀分布"。
方法2:
然后就会想到能否利用面积这个概念呢?因为上一个方法出错在边缘处,即y的范围会随着x的范围的变化而发生变化,所以如果在一个矩形区域内生成随机点,就会是均匀分布的;然后如果在圆内就保留下来这个点:
def random_point_in_circle(point_num, radius):
for i in range(2,point_num+1):
while True:
x=random.uniform(-radius,radius)
y=random.uniform(-radius,radius)
if(x**2)+(y**2)<(radius**2):
break
plt.plot(x,y,'*',color="blue")
def main():
pi = np.pi
theta = np.linspace(0, pi * 2, 1000)
R = 1
x = np.sin(theta) * R
y = np.cos(theta) * R
plt.figure(figsize=(6, 6))
plt.plot(x, y, label="cycle", color="green", linewidth=2)
plt.title("random_points_in_circle")
random_point_in_circle(4000, R)
plt.legend()
plt.show()
if __name__=="__main__":
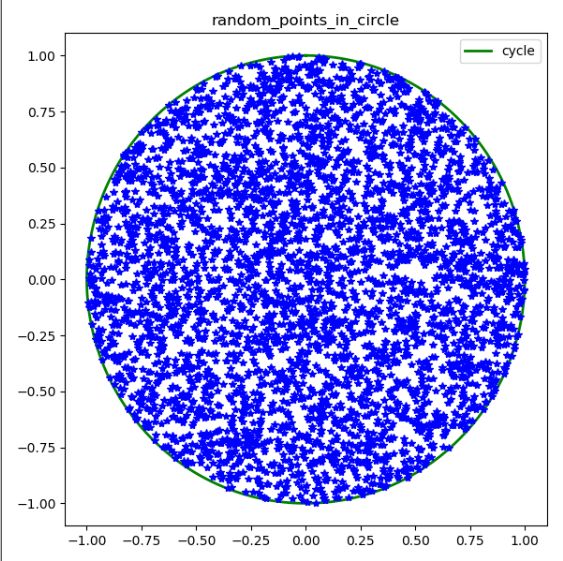
main()效果很OK:
但是这种方法的缺点就是会有较大的开销,想想看我们是按矩形范围内产生的点,最后会在圆内的点的概率只有\(\frac{\pi R^{2}}{(2R)^{2}}=\frac{\pi}{4}\)
### 方法3:
那么我们能否考虑用极坐标呢,可以消除y的范围对x的范围敏感的问题。利用\(x=R*cos(\theta)\)与\(y=R*sin(\theta)\),先随机生成[\(0,2\pi\)]内的\(\theta\),然后随机生成[0,R]内的r:
def random_point_in_circle(point_num, radius):
for i in range(2,point_num+1):
theta=random.random()*2*np.pi
r=random.uniform(0,radius)
x=r*math.cos(theta)
y=r*math.sin(theta)
plt.plot(x,y,'*',color="blue")
def main():
pi = np.pi
theta = np.linspace(0, pi * 2, 1000)
R = 1
x = np.sin(theta) * R
y = np.cos(theta) * R
plt.figure(figsize=(6, 6))
plt.plot(x, y, label="cycle", color="green", linewidth=2)
plt.title("random_points_in_circle")
random_point_in_circle(4000, R) # 修改此处来显示不同算法的效果
plt.legend()
plt.show()
if __name__=="__main__":
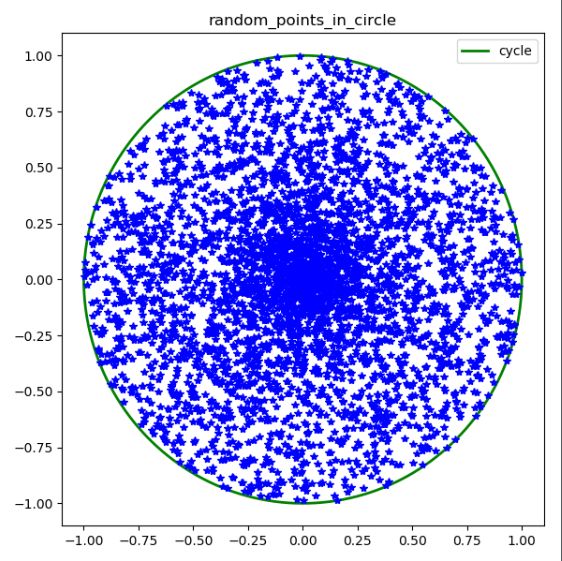
main()边缘的点会比较稀疏的原因是这样的,由于r是在[0,R]之间等概率产生的,所以可以认为同一个r的生成的随机点是相同的,但是圆的半径会变大,同样数量的点就会显得稀疏了。
方法4:
在这里我们先引入一条定理:令\(R=r^{2}\),R在[0,1]上是均匀分布,\(\theta\)在[\(0,2\pi\)]上是均匀分布,且R与\(\theta\)相互独立,令\[x=r*cos(\theta)=\sqrt{R}*cos(\theta)\]
\[y=r*sin(\theta)=\sqrt{R}*sin(\theta)\]
那么我们有(x,y)是均匀分布。
如果要证明(x,y)是均匀分布,由对称性我们只需要证明(x,y)在第一象限为均匀分布即可,即需要证明(x,y)的联合概率密度\(f(x,y)=\frac{1}{S}=\frac{1}{\pi /4}\)
首先我们知道连续性随机向量变换的联合分布的一个定理:
设(X,Y)是联合概率密度为\(f(x,y)\)的连续性随机向量,\(g_{1}(x,y),g_{2}(x,y)\) \(\xi=g_{1}(X,Y), \eta=g_{2}(X,Y)\)。如果对任何非负连续的二元函数\(h(\mu,\upsilon)\)成立,则有:
\[\iint h[g_{1}(x,y),g_{2}(x,y)]f(x,y)dx dy=\iint h(\mu,\upsilon)p(\mu,\upsilon)d\mu d\upsilon\]
放上代码:
def random_point(car_num,radius):
for i in range(1, car_num + 1):
theta = random.random() * 2 * np.pi
r = random.uniform(0, radius)
x = math.cos(theta) * (r ** 0.5)
y = math.sin(theta) * (r ** 0.5)
plt.plot(x, y, '*', color="blue")
def main():
pi = np.pi
theta = np.linspace(0, pi * 2, 1000)
R = 1
x = np.sin(theta) * R
y = np.cos(theta) * R
plt.figure(figsize=(6, 6))
plt.plot(x, y, label="cycle", color="green", linewidth=2)
plt.title("random_points_in_circle")
random_point(4000, R) # 修改此处来显示不同算法的效果
plt.legend()
plt.show()
if __name__=="__main__":
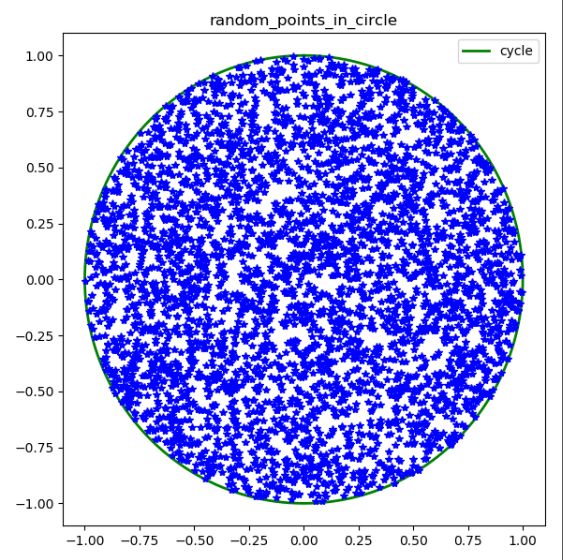
main()结果如下:
应该是比较满意的了。