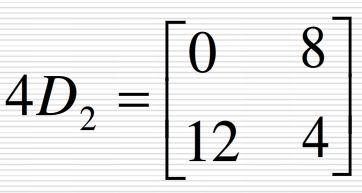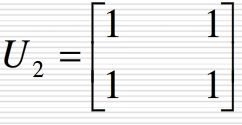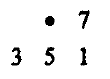数字加网(三)— —调频加网算法及实现
数字加网(一)— —概念及分色合成
数字加网(二)— —调幅加网算法及实现
数字加网(三)— —调频加网算法及实现
调频加网算法主要是抖动法与误差扩散法,前者又可以分为有序抖动和无序抖动,是点过程;后者是相邻过程。
有序抖动算法
Bayer抖动算法
算法公式
最具代表性的有序抖动算法,是1973年Bayer提出的Bayer算法,其递推公式如下:
令D1=0,n=2可以求出抖动矩阵
然后就可以继续推导出D4的抖动矩阵,推导过程如下
同理,我们可以推出D8的抖动矩阵
【注】一般处理采用D8的抖动矩阵
Python代码
### Digital Screening
### Author: Sin_Geek
### Date: 2015-05-17
from PIL import Image
time = 8
K = 8
L = 8
N = 63
im = Image.open('lena0.jpg').convert('L')
im2 = Image.new("1",(im.size[0]*time,im.size[1]*time))
#Bayer Ordered Dithering
Mask=[0,32,8,40,2,34,10,42,
48,16,56,42,50,18,58,26,
12,44,4,36,14,46,6,38,
60,28,52,20,62,30,54,22,
3,35,11,43,1,33,9,41,
51,19,59,27,49,17,57,25,
15,47,7,39,13,45,5,37,
63,31,55,23,61,29,53,21]
for m in range(im2.size[1]):
k = m % K
for n in range(im2.size[0]):
l = n % L
pix = int(im.getpixel((m/time,n/time))/255.0*N+0.5)
if pix > Mask[k*L+l]:
im2.putpixel((m,n),1)
else:
im2.putpixel((m,n),0)
im2.save("FM_Bayer.bmp")效果图
Halftone抖动算法
算法公式
其抖动矩阵如下:
Python代码
### Digital Screening
### Author: Sin_Geek
### Date: 2015-05-17
from PIL import Image
time = 8
K = 8
L = 8
N = 63
im = Image.open('lena0.jpg').convert('L')
im2 = Image.new("1",(im.size[0]*time,im.size[1]*time))
#Halftone Ordered Dithering
Mask=[28,10,18,26,36,44,52,34,
22,2,4,12,48,58,60,42,
14,6,0,20,40,56,62,50,
24,16,8,30,32,54,46,38,
37,45,53,35,29,11,19,27,
49,59,61,43,23,3,5,13,
41,57,63,51,15,7,1,21,
33,55,47,39,25,17,9,31]
for m in range(im2.size[1]):
k = m % K
for n in range(im2.size[0]):
l = n % L
pix = int(im.getpixel((m/time,n/time))/255.0*N+0.5)
if pix > Mask[k*L+l]:
im2.putpixel((m,n),1)
else:
im2.putpixel((m,n),0)
im2.save("FM_Halftone.bmp")效果图
Screw抖动算法
算法公式
其抖动矩阵如下:
Python代码
### Digital Screening
### Author: Sin_Geek
### Date: 2015-05-17
from PIL import Image
time = 8
K = 8
L = 8
N = 63
im = Image.open('lena0.jpg').convert('L')
im2 = Image.new("1",(im.size[0]*time,im.size[1]*time))
#Screw Ordered Dithering
Mask=[64,53,42,26,27,43,54,61,
60,41,25,14,15,28,44,55,
52,40,13,5,6,16,29,45,
39,24,12,1,2,7,17,30,
38,23,11,4,3,8,18,31,
51,37,22,10,9,19,32,41,
59,50,36,21,20,33,47,56,
63,58,49,35,34,48,57,62]
for m in range(im2.size[1]):
k = m % K
for n in range(im2.size[0]):
l = n % L
pix = int(im.getpixel((m/time,n/time))/255.0*N+0.5)
if pix > Mask[k*L+l]:
im2.putpixel((m,n),1)
else:
im2.putpixel((m,n),0)
im2.save("FM_Screw.bmp")效果图
CoarseFatting抖动算法
算法公式
其抖动矩阵如下:
Python代码
### Digital Screening
### Author: Sin_Geek
### Date: 2015-05-17
from PIL import Image
time = 8
K = 8
L = 8
N = 63
im = Image.open('lena0.jpg').convert('L')
im2 = Image.new("1",(im.size[0]*time,im.size[1]*time))
#CoarseFatting Ordered Dithering
Mask=[4,14,52,58,56,45,20,6,
16,26,38,50,48,36,28,18,
43,35,31,9,11,25,33,41,
61,46,23,1,3,13,55,60,
57,47,21,7,5,15,53,59,
49,37,29,19,17,27,39,51,
10,24,32,40,42,34,30,8,
2,12,54,60,51,44,22,0]
for m in range(im2.size[1]):
k = m % K
for n in range(im2.size[0]):
l = n % L
pix = int(im.getpixel((m/time,n/time))/255.0*N+0.5)
if pix > Mask[k*L+l]:
im2.putpixel((m,n),1)
else:
im2.putpixel((m,n),0)
im2.save("FM_CoarseFatting.bmp")效果图
无序抖动算法
所谓的无序抖动,指的就是生成抖动矩阵的过程是无序随机的,但是在计算机里一般使用的是伪随机的方法,一般有平方取中法、乘同余发生器、素数模乘同余法、组合乘同余法等,但是都不能取得满意的效果,其原因是无论怎样产生随机数,由于最大点距和最小点距不受控制,都有不规则聚集现象。所以,纯理论的随机加网算法是行不通的。下面只展示两种伪随机的方法,仅仅只为看看效果~
全局伪随机抖动算法
算法公式
即抖动矩阵为图像大小,矩阵里的值全部使用伪随机生成。
Python代码
### Digital Screening
### Author: Sin_Geek
### Date: 2015-05-17
from PIL import Image
import random
time = 8
K = 8
L = 8
N = 63
im = Image.open('lena0.jpg').convert('L')
im2 = Image.new("1",(im.size[0]*time,im.size[1]*time))
for m in range(im2.size[1]):
k = m % K
for n in range(im2.size[0]):
l = n % L
pix = int(im.getpixel((m/time,n/time))/255.0*N+0.5)
if pix > random.randint(0,64):
im2.putpixel((m,n),1)
else:
im2.putpixel((m,n),0)
im2.save("FM_Random.bmp")效果图
局部伪随机抖动算法
算法公式
在这抖动矩阵取的是8阶的,矩阵里的值使用伪随机生成。
Python代码
### Digital Screening
### Author: Sin_Geek
### Date: 2015-05-17
from PIL import Image
import random
time = 8
K = 8
L = 8
N = 63
im = Image.open('lena0.jpg').convert('L')
im2 = Image.new("1",(im.size[0]*time,im.size[1]*time))
Mask = [0]*im.size[0]*time*im.size[1]*time
for i in range(63):
Mask[i] = random.randint(0,64)
for m in range(im2.size[1]):
k = m % K
for n in range(im2.size[0]):
l = n % L
pix = int(im.getpixel((m/time,n/time))/255.0*N+0.5)
if pix > Mask[k*L+l]:
im2.putpixel((m,n),1)
else:
im2.putpixel((m,n),0)
im2.save("FM_Random_1.bmp")效果图
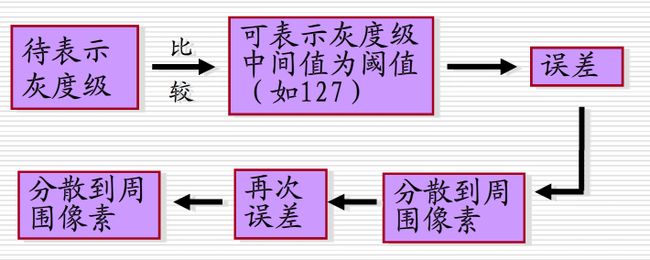
误差扩散算法
在原图像的归一化采集输入信号中加入误差过滤器的输出值得到信号值。然后进行阈值处理可得到表示信号。把在表示信号产生中出现的误差扩散到周围相邻区域的信号,然后重复上述步骤。如图所示
Floyd-Steinberg算法
算法公式
误差扩散方式
Python代码
### Digital Screening
### Author: Sin_Geek
### Date: 2015-05-17
from PIL import Image
time = 8
N = 144
im = Image.open('lena0.jpg').convert('L')
im2 = Image.new("1",(im.size[0]*time,im.size[1]*time))
pix =[0.0]*im2.size[0]*im2.size[1]
for m in range(im2.size[1]):
for n in range(im2.size[0]):
pix[m*im2.size[0]+n] = im.getpixel((m/time,n/time))*N/255.0+0.5
for m in range(im2.size[1]-1):
for n in range(1,im2.size[0]-1):
if pix[m*im2.size[0]+n] <= 72:
nError = pix[m*im2.size[0]+n]
im2.putpixel((m,n),0)
else:
nError = pix[m*im2.size[0]+n]-N
im2.putpixel((m,n),1)
pix[m*im2.size[0]+n+1] += nError*7/16.0
pix[(m+1)*im2.size[0]+n-1] += nError*3/16.0
pix[(m+1)*im2.size[0]+n] += nError*5/16.0
pix[(m+1)*im2.size[0]+n+1] += nError*1/16.0
im2.save("FM_Floyd_Steinberg.bmp")效果图
蛇形Floyd-Steinberg算法
算法公式
扩散方式与Floyd-Steinberg算法一样,但扫描方式不同,Floyd-Steinberg算法是遵循从左到右,从上到下。换一种扫描方式就得到了蛇形Floyd-Steinberg算法,扫描的方式是类似蛇形,从左到右再从右到左,再从左道右循环下去
Python代码
### Digital Screening
### Author: Sin_Geek
### Date: 2015-05-17
from PIL import Image
time = 8
N = 144
im = Image.open('lena0.jpg').convert('L')
im2 = Image.new("1",(im.size[0]*time,im.size[1]*time))
pix =[0.0]*im2.size[0]*im2.size[1]
for m in range(im2.size[1]):
for n in range(im2.size[0]):
pix[m*im2.size[0]+n] = im.getpixel((m/time,n/time))*N/255.0+0.5
for m in range(im2.size[1]-1):
if m%2 == 1:
for n in range(1,im2.size[0]-1):
if pix[m*im2.size[0]+n] <= 72:
nError = pix[m*im2.size[0]+n]
im2.putpixel((m,n),0)
else:
nError = pix[m*im2.size[0]+n]-N
im2.putpixel((m,n),1)
pix[m*im2.size[0]+n+1] += nError*7/16.0
pix[(m+1)*im2.size[0]+n-1] += nError*3/16.0
pix[(m+1)*im2.size[0]+n] += nError*5/16.0
pix[(m+1)*im2.size[0]+n+1] += nError*1/16.0
else:
for n in range(im2.size[0]-2,0,-1):
if pix[m*im2.size[0]+n] <= 72:
nError = pix[m*im2.size[0]+n]
im2.putpixel((m,n),0)
else:
nError = pix[m*im2.size[0]+n]-N
im2.putpixel((m,n),1)
pix[m*im2.size[0]+n-1] += nError*7/16.0
pix[(m+1)*im2.size[0]+n+1] += nError*3/16.0
pix[(m+1)*im2.size[0]+n] += nError*5/16.0
pix[(m+1)*im2.size[0]+n-1] += nError*1/16.0
im2.save("FM_Floyd_Steinberg_Snake.bmp")效果图
Burkes算法
算法公式
扩散方式
Python代码
### Digital Screening
### Author: Sin_Geek
### Date: 2015-05-17
from PIL import Image
time = 8
N = 144
im = Image.open('lena0.jpg').convert('L')
im2 = Image.new("1",(im.size[0]*time,im.size[1]*time))
pix =[0.0]*im2.size[0]*im2.size[1]
for m in range(im2.size[1]):
for n in range(im2.size[0]):
pix[m*im2.size[0]+n] = im.getpixel((m/time,n/time))*N/255.0+0.5
for m in range(1,im2.size[1]-1):
for n in range(2,im2.size[0]-2):
if pix[m*im2.size[0]+n] <= 72:
nError = pix[m*im2.size[0]+n]
im2.putpixel((m,n),0)
else:
nError = pix[m*im2.size[0]+n]-N
im2.putpixel((m,n),1)
pix[m*im2.size[0]+n+1] += nError*8/32.0
pix[m*im2.size[0]+n+2] += nError*4/32.0
pix[(m+1)*im2.size[0]+n-2] += nError*2/32.0
pix[(m+1)*im2.size[0]+n-1] += nError*4/32.0
pix[(m+1)*im2.size[0]+n] += nError*8/32.0
pix[(m+1)*im2.size[0]+n+1] += nError*4/32.0
pix[(m+1)*im2.size[0]+n+2] += nError*2/32.0
im2.save("FM_Burkes.bmp")效果图
Jarris-Judice-Ninke算法
算法公式
扩散方式
Python代码
### Digital Screening
### Author: Sin_Geek
### Date: 2015-05-17
from PIL import Image
time = 8
N = 144
im = Image.open('lena0.jpg').convert('L')
im2 = Image.new("1",(im.size[0]*time,im.size[1]*time))
pix =[0.0]*im2.size[0]*im2.size[1]
for m in range(im2.size[1]):
for n in range(im2.size[0]):
pix[m*im2.size[0]+n] = im.getpixel((m/time,n/time))*N/255.0+0.5
for m in range(im2.size[1]-2):
for n in range(2,im2.size[0]-2):
if pix[m*im2.size[0]+n] <= 72:
nError = pix[m*im2.size[0]+n]
im2.putpixel((m,n),0)
else:
nError = pix[m*im2.size[0]+n]-N
im2.putpixel((m,n),1)
pix[m*im2.size[0]+n+1] += nError*7/48.0
pix[m*im2.size[0]+n+2] += nError*5/48.0
pix[(m+1)*im2.size[0]+n-2] += nError*3/48.0
pix[(m+1)*im2.size[0]+n-1] += nError*5/48.0
pix[(m+1)*im2.size[0]+n] += nError*7/48.0
pix[(m+1)*im2.size[0]+n+1] += nError*5/48.0
pix[(m+1)*im2.size[0]+n+2] += nError*3/48.0
pix[(m+2)*im2.size[0]+n-2] += nError*1/48.0
pix[(m+2)*im2.size[0]+n-1] += nError*3/48.0
pix[(m+2)*im2.size[0]+n] += nError*5/48.0
pix[(m+2)*im2.size[0]+n+1] += nError*3/48.0
pix[(m+2)*im2.size[0]+n+2] += nError*1/48.0
im2.save("FM_Jarris_Judice_Ninke.bmp")效果图
Stucki算法
算法公式
扩散方式
Python代码
### Digital Screening
### Author: Sin_Geek
### Date: 2015-05-17
from PIL import Image
time = 8
N = 144
im = Image.open('lena0.jpg').convert('L')
im2 = Image.new("1",(im.size[0]*time,im.size[1]*time))
pix =[0.0]*im2.size[0]*im2.size[1]
for m in range(im2.size[1]):
for n in range(im2.size[0]):
pix[m*im2.size[0]+n] = im.getpixel((m/time,n/time))*N/255.0+0.5
for m in range(im2.size[1]-2):
for n in range(2,im2.size[0]-2):
if pix[m*im2.size[0]+n] <= 72:
nError = pix[m*im2.size[0]+n]
im2.putpixel((m,n),0)
else:
nError = pix[m*im2.size[0]+n]-N
im2.putpixel((m,n),1)
pix[m*im2.size[0]+n+1] += nError*8/42.0
pix[m*im2.size[0]+n+2] += nError*4/42.0
pix[(m+1)*im2.size[0]+n-2] += nError*2/42.0
pix[(m+1)*im2.size[0]+n-1] += nError*4/42.0
pix[(m+1)*im2.size[0]+n] += nError*8/42.0
pix[(m+1)*im2.size[0]+n+1] += nError*4/42.0
pix[(m+1)*im2.size[0]+n+2] += nError*2/42.0
pix[(m+2)*im2.size[0]+n-2] += nError*1/42.0
pix[(m+2)*im2.size[0]+n-1] += nError*2/42.0
pix[(m+2)*im2.size[0]+n] += nError*4/42.0
pix[(m+2)*im2.size[0]+n+1] += nError*2/42.0
pix[(m+2)*im2.size[0]+n+2] += nError*1/42.0
im2.save("FM_Stucki.bmp")效果图
多位误差扩散算法
以Floyd-Steinberg算法为例,都是两位0和1,非黑即白。但是市场上出现了多位的打印机,于是随之而出的是多位的算法。即存在0,0.5,1。
算法公式
根据分为几位,划分区域,分别进行误差扩散,考虑到规律性条纹等问题,可以对划分区域进行一个随机值的添加,使得分割点不再是一个像素值,而是动态范围内的一个值,降低规律性。本示例中没有添加,读者可自行改进~~~
Python代码
### Digital Screening
### Author: Sin_Geek
### Date: 2015-05-17
from PIL import Image
import random
time = 8
N = 144
R = 2
M = R*2
im = Image.open('lena0.jpg').convert('L')
im2 = Image.new("L",(im.size[0]*time,im.size[1]*time))
pix = [0.0]*im2.size[0]*im2.size[1]
for m in range(im2.size[1]):
for n in range(im2.size[0]):
pix[m*im2.size[0]+n] = im.getpixel((m/time,n/time))*N/255.0+0.5
for m in range(1,im2.size[1]-1):
for n in range(1,im2.size[0]-1):
if pix[m*im2.size[0]+n] <= N/M:
nError = pix[m*im2.size[0]+n]
im2.putpixel((m,n),0)
elif pix[m*im2.size[0]+n] <= 3*N/M:
nError = pix[m*im2.size[0]+n]-2*N/M
im2.putpixel((m,n),255/R)
else:
nError = pix[m*im2.size[0]+n]-144
im2.putpixel((m,n),255)
pix[m*im2.size[0]+n+1] += nError*7/16.0
pix[(m+1)*im2.size[0]+n-1] += nError*3/16.0
pix[(m+1)*im2.size[0]+n] += nError*5/16.0
pix[(m+1)*im2.size[0]+n+1] += nError*1/16.0
im2.save("FM_Floyd_Steinberg_Multi_Threshold.bmp")