基于MATLAB的遗传算法优化的神经网络房价预测实战(附完整代码)
本文利用BP神经网络对美国波士顿的房价进行预测,并针对BP神经网络存在的易陷入局部极小值,收敛速度慢,网络拓扑结构不稳定等问题,提出运用GA遗传算法对BP神经网络的初始权值和阈值进行优化。分别对传统神经网络和GA_BP进行训练和仿真,结果表明,经遗传算法优化后的神经网络可以加快网络收敛速度,提高预测房价的精度。
- 概述
随着房地产市场行业快速迅猛的发展,人们越来越关注放价的走势。从宏观上来看,影响房价的因素分为房地产自身因素和房地产外部因素。自身因素主要包括:区位因素、实物因素和权益因素。外部因素主要包括:人口因素、制度因素、经济因素、社会因素和国际因素。由此可看出,影响房价的因素很多。在本文的研究中,我们只选取部分影响房价的因素进行分析。
人工神经网络是基于模仿人脑系统的结构和功能,反映人脑某些特性的一种智能信息处理系统。人工神经网络具有并行处理能力、自学习和自适应等特性。同时,它还具有非线性映射、优化计算、联想记忆等功能。目前,人工神经网络已经在很多领域得到了广泛的应用。这些应用领域主要包括智能检测、非线性预测、模式识别、机器人控制等。随着人工神经网络的进一步发展和更加深入的研究,人工神经网络应用的领域越来越广泛。因此,本文提出利用遗传算法优化的 BP 神经网络来建立房价预测模型。 - BP神经网络及遗传算法
BP 神经网络(Back Propagation Neural Network)也称为反向传播神经网络,是一种具有 3 层或 3 层以上结构的无反馈的、层内无互连的网络,其结构如图所示。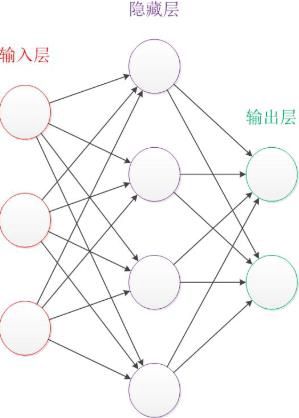
BP 神经网络除输入层和输出层外,还包括一个或多个隐含层,各个层神经元之间实现全连接,而同层内各神经元之间无连接。BP神经网络通过有指导的学习方式进行学习和训练。标准的BP学习算法采用误差函数按梯度下降的方法学习,使网络的实际输出值和期望输出值之间的均方误差最小。BP神经网络的学习过程主要是由输入信号正向传播和误差反向传播构成的。在正向传播时,输入信号从输入层输入,经过隐含层的逐层处理后,传递给输出层。若输出层的实际输出与期望输出不符,则转入误差反向传播过程。反向传播的过程就是由输出层向输入层逐层修正连接权值使误差减小。输入信号的正向传播与误差的反向传播过程是循环进行的。BP神经网络的训练过程就是不断调整连接权值的过程,这个过程进行到输出的均方误差达到要求的标准。
遗传算法(Genetic Algorithm, GA)是模拟生物在自然界进化过程中的遗传选择和自然淘汰的一种计算模型。它是一种具有很强的全局搜索能力和全局优化性能的算法。遗传算法主要包括选择、交叉和变异等操作。它的主要优点是鲁棒性强、简单通用,能够用于并行分布式处理。因此,将遗传算法与 BP 神经网络相结合,训练网络时先用遗传算法对神经网络的权值和阈值进行寻优,缩小搜索范围之后,再利用 BP 神经网络对问题进行求解。 - BP神经网络的房价预测模型设计
3.1数据选择
实验数据的选取对网络模型的预测结果影响很大,所以选取的样本数据要尽可能真实客观地反映房价的变化规律。选取的房价影响因素不仅要合理,而且还要具有代表性。分析影响房价的所有因素是不现实的,在本文的研究中,选取了13 个房价影响因素。我们使用的训练数据来自于美国,数据源地址为https://archive.ics.uci.edu/ml/machine-learning-databases/housing/。美国政府公开了很多公共数据以便社会研究,在我们使用的Keras框架中,包含了美国1970年波士顿郊区的房地产相关信息,例如犯罪率,房地产税,不同户型的房价等等。选取输入数据有以下13个
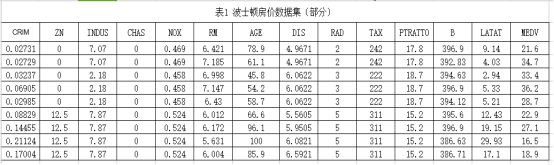
CRIM:城镇人均犯罪率
ZN:住宅用地所占比例
INDUS:城镇中非商业用地所占比例
CHAS:CHAS查尔斯河虚拟变量,用于回归分析
NOX:环保指标
RM:每栋住宅房间数
AGE:1940年前建成的自主单位比例
DIS:距离5个波士顿就业中心加权距离
RAD:距离高速公路的便利指数
TAX:每一万美元的不动产税率
PTRATIO:城镇中教师学生比例
B:城镇中黑人比例
LSTAT:城区多少百分比房东为低收入阶层
MEDV:自住房屋房价中位数
3.2数据预处理
本次选取数据来源有以下几个特点:第一,是数据量很小,数据总量共五百多条;第二,数据的格式不一样,有些数据以百分比来表示,有些数据处于范围1到12,而有些数据范围在0到100,因此首先需要对数据进行预处理。由于不同的数据有不同的数量级,因此为了提高网络运算速率,便于网络计算以及提高预测的准确性,需要对数据进行归一化处理。基于MATLAB我们采用mapminmax函数,输入样本归一化为:
[pn_train,ps1] = mapminmax(p_train’);
pn_test = mapminmax(‘apply’,p_test’,ps1);
其中PS1是训练样本的数据的映射,记录了训练集的归一化方法,即PS1中包含了训练数据的最大值和最小值,式中pn_test是测试样本,对于测试样本来说,预处理应该和训练样本一致,即测试样本的最大值和最小值应该是训练集的最大值与最小值。对于测试集需要同样用ps1方法进行归一化。
3.3数据建模
3.3.1 初始化参数设定
本文采用newff来创建网络,设置隐藏神经元个数为5个,训练网络性能所采用的的函数为trainlm默认函数,其适合中型网络,对内存的需求大,但收敛速度快。设置训练次数为20000次,收敛误差为0.0000001,。初始的权值和阈值为系统默认值。
3.3.2 隐含节点数确定
本文实验选取3 层结构的BP 神经网络进行预测模型的建立。若隐层节点数太少,网络可能无法训练或性能很差;若隐层节点数太多,虽然可减小网络的系统误差,但网络训练时间延长,并且训练容易陷入局部极小点而得不到最优点,也是训练时出现“过拟合”的内在原因。因此,合理隐层节点数应在综合考虑网络结构复杂程度和误差大小的情况下用节点删除法和扩张法确定。BP神经网络的隐含层节点通常用试凑法确定,可以先设置较少的隐含层节点来训练网络,然后逐渐增加隐含层节点数,使用同一样本集进行训练,最终选取网络误差最小时对应的隐含层节点数。在实验中,往往根据经验公式得到一个粗略的估计值作为初始值,再用试凑法确定最佳节点数。常用的经验公式为:
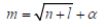
其中,n为输入层节点数
3.4模型训练与仿真
采用Matlab作为软件平台,利用神经网络工具箱函数编程实现BP神经网络预测模型的构建、训练和仿真。将收集到的样本分为2 个部分:选取前80%作为训练样本,剩下的20%数据作为测试验证样本。 - 经遗传算法优化的BP神经网络模型
遗传算法是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化的计算模型,是一种通过模拟自然进化过程搜索最优解的方法。由于BP神经网路的学习收敛速度太慢,易陷入局部极小值,网络拓扑结构不稳定等问题,因此用遗传算法优化的BP神经网络模型(GA-BP神经网络)。GA用于函数优化的目的就是发现问题的全局最优解,以此来提高预测的精度。
4.1参数的选取
在BP神经网络中,隐层节点数的选择非常重要,他不仅很大影响了神经网络模型的性能,而且是训练时出现“过拟合”的直接原因。确定隐含层基本条件有两点:第一,隐层节点数必须小于N-1;第二,训练样本必须多余网络模型的连接权重,一般为2到10倍。对于本次实验,GA-BP神经网络采用3层网络结构,输入层神经元个数为13,隐含层神经元个数为13,输出层神经元的个数为1。
4.2GA-BP神经网络优化的实验步骤
GA-BP神经网络的实现步骤为:
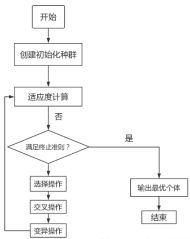
(1)个体编码与创建初始化种群
遗传算法是对群体进行的进化操作,设置迭代次数为100次,种群规模为10,对个体编码长度规则为:
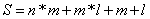
其中,m为隐含层节点数,n为输入层节点数,l为输出层节点数。
(2)适应度计算
此处我们调用fun函数实现对其适应度的计算,神经网络的预测误差越小,对应的适应度函数就越小,适应度就越好。
(3)交叉和变异操作
交叉运算是遗传算法中产生新个体的主要操作过程,变异运算是对个体的某一个或某一些基因座上的基因值按某一较小的概率进行改变,也是产生新个体的一种方法。对于最优个体没有进行交叉操作,而是直接复制到下一代。通常设置交叉和变异概率为0到1之间,此处取变交叉概率为0.3,变异概率为0.1。 - 实验结果分析
如图所示为没有加入遗传算法的BP神经网络预测结果,其中平均预测误差为0.5754,预测均方误差:4.6101
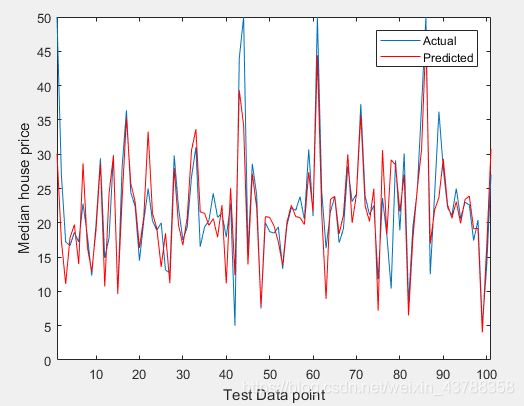
如图所示为加入遗传算法的BP神经网络预测效果图,我们可以得到平均误差为0.30583,均方误差为3.7968。
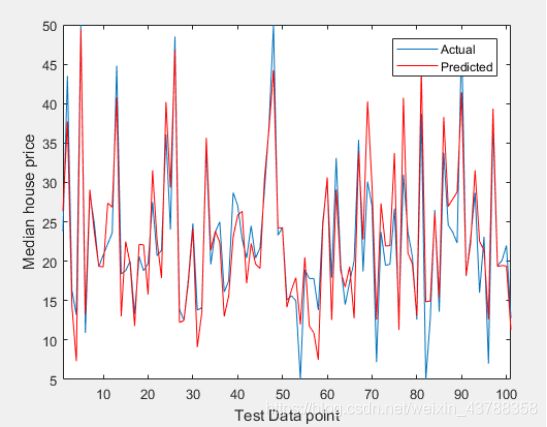
如图 所示为得到的适应度曲线,此处适应度代表预测值与实际值的差值,在进化代数接近60的时候达到了最优适应度。
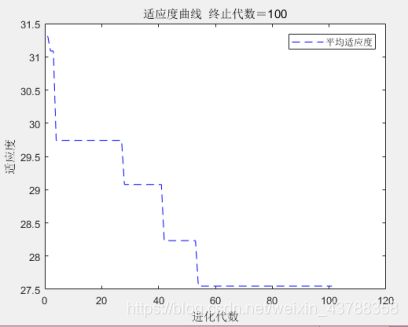
- 结束语
传统的BP神经网络存在收敛速度慢,容易陷入局部极小值的问题,因此将遗传算法与 BP 神经网络相结合,训练网络时先用遗传算法对神经网络的权值和阈值进行寻优,缩小搜索范围之后,再利用 BP 神经网络对问题进行求解。根据得到的仿真结果表示,利用GA-BP神经网络预测房价,可以很大程度上提高收敛速度,同时提高预测的准确度。 - 完整代码
clc
clear
%
%% 网络结构建立
%读取数据
filename = 'housing.txt';
inputNames = {'CRIM','ZN','INDUS','CHAS','NOX','RM','AGE','DIS','RAD','TAX','PTRATIO','B','LSTAT'};
outputNames = {'MEDV'};
housingAttributes = [inputNames,outputNames];
%%Import Data
formatSpec = '%8f%7f%8f%3f%8f%8f%7f%8f%4f%7f%7f%7f%7f%f%[^\n\r]';
fileID = fopen(filename,'r');
dataArray = textscan(fileID, formatSpec, 'Delimiter', '', 'WhiteSpace', '', 'ReturnOnError', false);
fclose(fileID);
housing = table(dataArray{1:end-1}, 'VariableNames', {'VarName1','VarName2','VarName3','VarName4','VarName5','VarName6','VarName7','VarName8','VarName9','VarName10','VarName11','VarName12','VarName13','VarName14'})
%%Read into a Table
housing.Properties.VariableNames = housingAttributes;
features = housing{:,inputNames};
prices = housing{:,outputNames};
%节点个数
inputnum=13; %输入层节点数
hiddennum=13;%隐含层节点数
outputnum=1; %输出层节点数
%训练数据和预测数据
len = length(prices);
index = randperm(len);%生成1~len 的随机数
%input_train = features(index(1:round(len*0.8)),:);%训练样本输入
%output_train = prices(index(1:round(len*0.8)),:);%训练样本输出
%input_test = features(index(round(len*0.8)+1:end),:);%测试样本输入
%output_test = prices(index(round(len*0.8)+1:end),:);%测试样本输出
input_train=features(index(1:405),:)';
input_test=features(index(406:506),:)';
output_train=prices(index(1:405))';
output_test=prices(index(406:506))';
%选连样本输入输出数据归一化
[inputn,inputps]=mapminmax(input_train);
[outputn,outputps]=mapminmax(output_train);
%构建网络
net=newff(inputn,outputn,hiddennum);
%% 遗传算法参数初始化
maxgen=100; %进化代数,即迭代次数
sizepop=10; %种群规模
pcross=[0.3]; %交叉概率选择,0和1之间
pmutation=[0.1]; %变异概率选择,0和1之间
%节点总数
numsum=inputnum*hiddennum+hiddennum+hiddennum*outputnum+outputnum;
lenchrom=ones(1,numsum);
bound=[-2*ones(numsum,1) 2*ones(numsum,1)]; %数据范围
%--------------------------------------种群初始化--------------------------------------------------------
individuals=struct('fitness',zeros(1,sizepop), 'chrom',[]); %将种群信息定义为一个结构体
avgfitness=[]; %每一代种群的平均适应度
bestfitness=[]; %每一代种群的最佳适应度
bestchrom=[]; %适应度最好的染色体
%初始化种群
for i=1:sizepop
%随机产生一个种群
individuals.chrom(i,:)=Code(lenchrom,bound); %编码(binary和grey的编码结果为一个实数,float的编码结果为一个实数向量)
%Code函数用于编码,lenchrom是染色体长度,bound是变量的取值范围
x=individuals.chrom(i,:);
%计算适应度
individuals.fitness(i)=fun(x,inputnum,hiddennum,outputnum,net,inputn,outputn); %染色体的适应度
%fun函数(BP神经网络预测,记录预测误差,inputn为训练输入数据,outputn为训练输出数据)
end
%找最好的染色体
[bestfitness bestindex]=min(individuals.fitness);
bestchrom=individuals.chrom(bestindex,:); %最好的染色体
avgfitness=sum(individuals.fitness)/sizepop; %染色体的平均适应度
% 记录每一代进化中最好的适应度和平均适应度
trace=[avgfitness bestfitness];
%% 迭代求解最佳初始阀值和权值
% 进化开始
for i=1:maxgen
disp(['遗传迭代第',num2str(i),'次'])
% 选择
individuals=Select(individuals,sizepop);
avgfitness=sum(individuals.fitness)/sizepop;
%交叉
individuals.chrom=Cross(pcross,lenchrom,individuals.chrom,sizepop,bound);
% 变异
individuals.chrom=Mutation(pmutation,lenchrom,individuals.chrom,sizepop,i,maxgen,bound);
% 计算适应度
for j=1:sizepop
x=individuals.chrom(j,:); %解码
individuals.fitness(j)=fun(x,inputnum,hiddennum,outputnum,net,inputn,outputn);
end
%找到最小和最大适应度的染色体及它们在种群中的位置
[newbestfitness,newbestindex]=min(individuals.fitness);
[worestfitness,worestindex]=max(individuals.fitness);
% 代替上一次进化中最好的染色体
if bestfitness>newbestfitness
bestfitness=newbestfitness;
bestchrom=individuals.chrom(newbestindex,:);
end
individuals.chrom(worestindex,:)=bestchrom;
individuals.fitness(worestindex)=bestfitness;
avgfitness=sum(individuals.fitness)/sizepop;
trace=[trace;avgfitness bestfitness]; %记录每一代进化中最好的适应度和平均适应度
end
%% 遗传算法结果分析
figure(1)
[r c]=size(trace);
plot([1:r]',trace(:,2),'b--');
title(['适应度曲线 ' '终止代数=' num2str(maxgen)]);
legend({'平均适应度','最佳适应度'});
xlabel('进化代数');
ylabel('适应度');
x=bestchrom;
%% 把最优初始阀值权值赋予网络预测
% %用遗传算法优化的BP网络进行值预测
w1=x(1:inputnum*hiddennum);
B1=x(inputnum*hiddennum+1:inputnum*hiddennum+hiddennum);
w2=x(inputnum*hiddennum+hiddennum+1:inputnum*hiddennum+hiddennum+hiddennum*outputnum);
B2=x(inputnum*hiddennum+hiddennum+hiddennum*outputnum+1:inputnum*hiddennum+hiddennum+hiddennum*outputnum+outputnum);
net.iw{1,1}=reshape(w1,hiddennum,inputnum);
net.lw{2,1}=reshape(w2,outputnum,hiddennum);
net.b{1}=reshape(B1,hiddennum,1);
net.b{2}=B2;
%% BP网络训练
%网络进化参数
net.trainParam.epochs=20000;
net.trainParam.lr=0.1;
net.trainParam.goal=0.00001;
%网络训练
[net,per2]=train(net,inputn,outputn);
%% BP网络预测
%数据归一化
inputn_test=mapminmax('apply',input_test,inputps);
an=sim(net,inputn_test);
test_simu=mapminmax('reverse',an,outputps);
error=test_simu-output_test;
disp(['平均误差=',num2str(mean(error)) ' 均方误差=',num2str(std(error))])
figure(2);
plot(output_test);
hold on;
plot(test_simu,'r');
xlim([1 length(output_test)]);
hold off;
legend({'Actual','Predicted'})
xlabel('Test Data point');
ylabel('Median house price');