Gray格雷码（原先有问题，改过来了）

减治、分治和变治策略的算法设计、实现与分析

掌握分治法、减治法和变治法的设计思想；

掌握分治法的求解步骤；

掌握分治法解题的算法框架。

格雷码构造问题

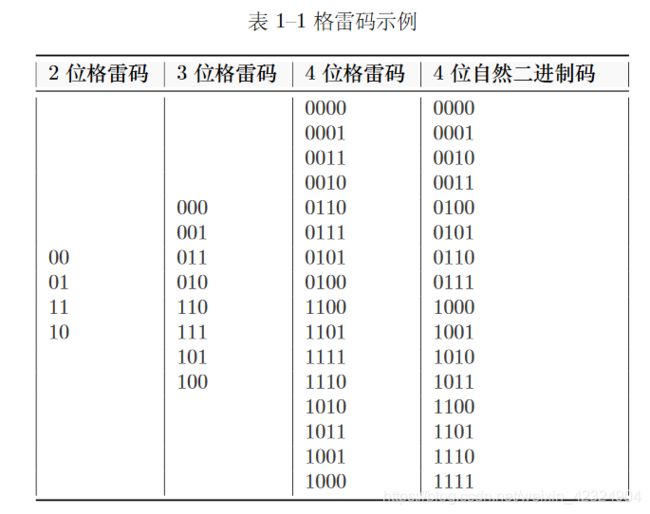
1.3.1问题描述Gray玛是一个长度为2n的序列。序列无相同元素，每个元素都是长度为n的串，相邻元素恰好只有一位不同。试设计一个算法对任意n构造相应的Gray码。（分治、减治、变治皆可）格雷码是反射码，例子可以参见表1–1。我们可以利用递归的如下规则来构造：

1.3.2问题的形式化尽量使用数学语言对原问题进行抽象化。1.4算法设计1.4.1算法描述针对形式化后的抽象问题，使用伪代码对求解算法进行描述。要求必须包含算法的输入和输出，并给出算法涉及的关键步骤。

看到一个博客，里面讲到一个规律，写的非常好。利用这个规律就可以做出来，我在这里写个博客纪念一下。同时也为加深印象增强理解。

 

这是问题，那么核心规律是什么呢？

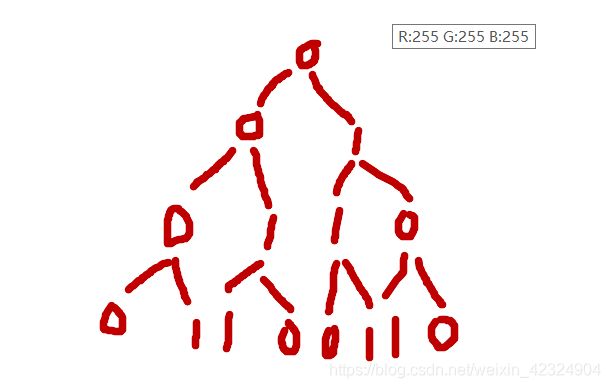
就是其看成二叉树。

每一个数字，如果他的爷爷节点是0，那它左边的就和它的爸爸节点一样。祖传染色体变异了。

也就是说，我们考虑是否可以这样描述。

if(!a[k-2]) a[k] = a[k-1];
else a[k] = !a[k-1];

好像是可以的。不妨试一试。

 

如果试过了就会发现有些问题，那就是，最下面一层每一个叉叉分支，只能表示左边的那个，右边那个正好相反的。那么这个时候可以用到一个参数，将其传进去。不好描述了，上代码吧，这个参数就是Gray（int k,int flag)里的flag。不是0就是1；

如果这里觉得我没表达清楚，那就别看了。往下看。

思想如下。

也就是为什么主函数要从2开始，直接传2；

一目了然，不言自喻。但是还是要稍微说明一下，就是，为什么要在前面添加那两个累赘的0？

因为我们前面说到的利用那个核心规律，要用到爷爷节点，那既然这个树是带递归性质的，我们何不把第一个节点当作别人的孙子呢？一个人的爷爷，必定也是这人爷爷的孙子。所以，这样就可以利用到它的爷爷节点的性质了。

#include
using namespace std;
#define N 50
int n;
int a[N] = {0};
void Gray(int k,int flag)
{
	if(!a[k-2]) a[k] = flag;
	else a[k] = !flag;
	if(k == n+1){
		for(int i=2;i

if(k == n+1){
		for(int i=2;i

那么这一段是用来做什么的呢？是用来判断的，如果k也就是层次，到达了我们需要的那一层，比如输入3，从a[2]开始算起，那么a[2],a[3],a[4]，k=4时这就是我们需要的。也就是说，if(k==n+1),就输出。

这个函数，怎么利用到分治思想？

Gray(k+1,flag);
Gray(k+1,!flag);

就是这里。

也就是刚才为什么要利用一个flag而不是直接利用爸爸节点a[k-1]的关系.

递归这个不好描述，只能说用递归就不能钻牛角尖。了解这个函数干嘛用的，然后直接用他。终止条件是什么，闹清楚以后直接用。不用管其中实现细节。

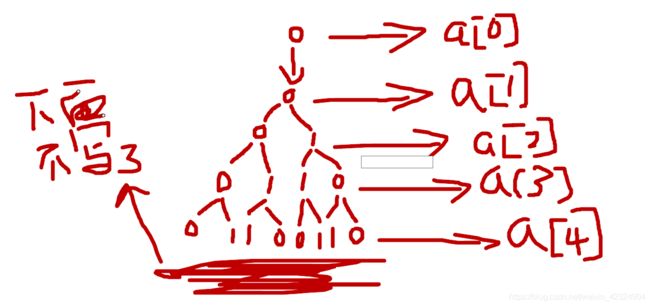
不好意思，没有仔细核对答案，有个问题没发现。就是这个结果出来以后，只有最高位是0的情况，而没有最高为是1的情况。也就是，问题在于原来的根节点应该再往后退一个，以第三层的那个作为根节点。

错误的原因在于，从第a[2]层开始，第a[2]层就是0，没有1，而利用了Gray(k+1,flag)和Gray（k+1,!flag)的第三层是一枝往上走的，从第三层开始输出就很好了。

#include
using namespace std;
#define N 50
int n;
int a[N] = {0};
int tab = 0;
void Gray(int k,int flag)
{
	if(!a[k-2]) a[k] = flag;
	else a[k] = !flag;
	if(k == n+2){
		for(int i=3;i<=n+2;i++){
			printf("%d",a[i]);
		}
		printf("\t%d",++tab);
		printf("\n");
		return ;
	}
	Gray(k+1,flag);
	Gray(k+1,!flag);
}
int main()
{
	scanf("%d",&n);
	Gray(2,0);
	return 0;
}