SDU 程序设计思维实践 第四周 csp模拟

题目A - 咕咕东的奇遇

题意

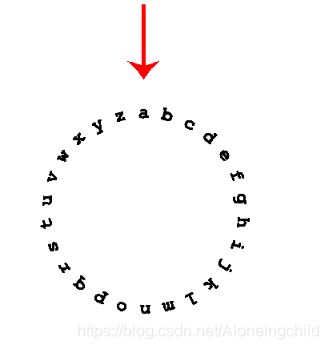
咕咕东是个贪玩的孩子，有一天，他从上古遗迹中得到了一个神奇的圆环。这个圆环由字母表组成首尾相接的环，环上有一个指针，最初指向字母a。咕咕东每次可以顺时针或者逆时针旋转一格。例如，a顺时针旋转到z，逆时针旋转到b。咕咕东手里有一个字符串，但是他太笨了，所以他来请求你的帮助，问最少需要转多少次。

Input

zeus

Output

18

思路

考虑上衣字符拨到当前字符逆时针还是顺时针即可。

具体的判断可以用，注意取模：

• 顺时针： 当前字符$-$ 上一字符
• 逆时针：26$-$ (当前字符$-$ 上一字符)

总结

憨憨的我上来直接24个英文字母。签到题

代码

#include 
#include 
using namespace std;
int main() {
     
    string s;
    cin >> s;
    int ans = 0;
    int k = 0;
    for (int i = 0; i < s.size(); i++) {
     
        int cur = (26 + s[i] - 'a' - k) % 26;
        // ans += min((s[i] - 'a' - k) % 26, 26 - ((s[i] - 'a' - k) % 26));
        ans += min(cur, 26 - cur);
        k = s[i] - 'a';
        // cout << k << " " << ans << endl;
    }
    cout << ans;
    return 0;
}

题目B - 咕咕东想吃饭

题意

咕咕东考试周开始了，考试周一共有$n$天。他不想考试周这么累，于是打算每天都吃顿好的。他决定每天都吃生煎，咕咕东每天需要买$a_i$个生煎。但是生煎店为了刺激消费，只有两种购买方式：①在某一天一次性买两个生煎。②今天买一个生煎，同时为明天买一个生煎，店家会给一个券，第二天用券来拿。没有其余的购买方式，这两种购买方式可以用无数次,但是咕咕东是个节俭的好孩子，他训练结束就走了，不允许训练结束时手里有券。咕咕东非常有钱，你不需要担心咕咕东没钱，但是咕咕东太笨了，他想问你他能否在考试周每天都能恰好买$a_i$个生煎。

其中

$(1\le n\le 100000)$，$(1\le a_i\le 10000)$

Input

4
1 2 1 2

Output

2

思路

考虑对于第$i$天，假设买了m个煎饼，其第二种方案对第$i+1$天的影响可以转变为至多一次。

因为，假设第$i$天选了2次方案二，其等价于第$i$天选1次方案一，第$i+1$天选1次方案一。

故问题可以转化为先考虑最后一天，若为偶数个，直接全选择方案1，若为奇数个，选择一次方案1。并让前一天总煎饼数-1（选择一次方案2）。

---

则问题转化为，对于当前天：

• 若煎饼数为偶数，则继续。
• 若煎饼数为基数，则令前一天煎饼数-1。

输出NO的情况为当前天煎饼数$<0$ ，或第一天煎饼数为基数个。否则输出YES。

总结

这题还是挺有意思的，不过数据有点水（逃） 。全输出YES能拿到不少分吧。

代码

#include 
#include 
#include 
#include 
#include 
using namespace std;
int v[100010];
int main() {
     
    int n;
    cin >> n;
    for (int i = 1; i <= n; i++) {
     
        cin >> v[i];
    }
    int flag = 0;
    for (int i = n; i; i--) {
     
        if (flag == 1) {
     
            v[i] -= 1;
            if (v[i] < 0) {
     
                cout << "NO";
                return 0;
            }
        }
        if (v[i] % 2 == 0) {
     
            flag = 0;
        } else {
     
            flag = 1;
        }
    }
    if (flag == 1) {
     
        cout << "NO";
    } else {
     
        cout << "YES";
    }
    return 0;
}

题目C - 可怕的宇宙射线

题意

众所周知，瑞神已经达到了CS本科生的天花板，但殊不知天外有天，人外有苟。在浩瀚的宇宙中，存在着-种叫做苟狗的生物， 这种生物天生就能达到人类研究生的知识水平，并且天生擅长CSP,甚至有全国第一的水平!但最可怕的是，它可以发出宇宙射线!宇宙射线可以摧毁人的智商，进行降智打击!

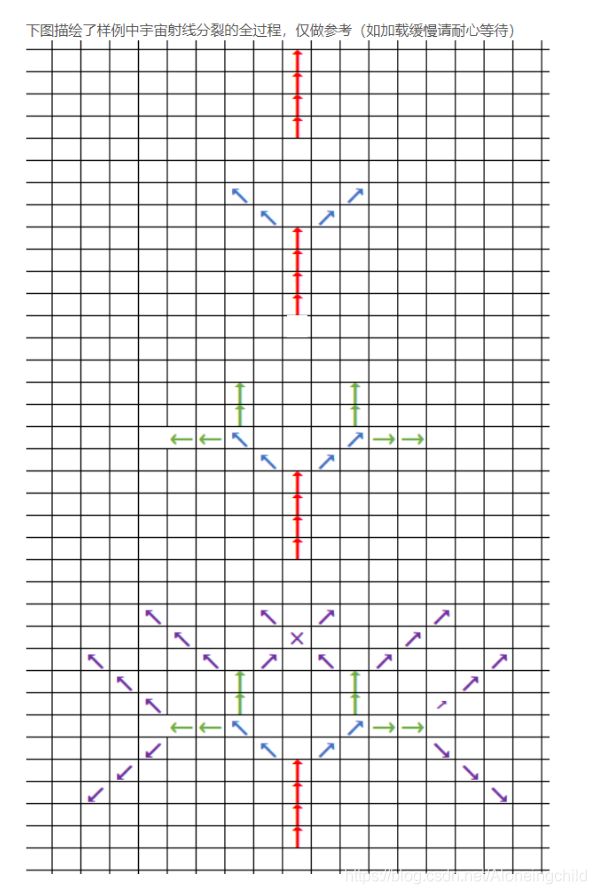
宇宙射线会在无限的二维平面上传播(可以看做一个二维网格图)，初始方向默认向上。宇宙射线会在发射出一段距离后分裂,向该方向的左右$45^{\circ }$方向分裂出两条宇宙射线，同时威力不变!宇宙射线会分裂$n$次,每次分裂后会在分裂方向前进$a$个单位长度。

现在瑞神要带着他的小弟们挑战苟狗，但是瑞神不想让自己的智商降到普通本科生zjm那么菜的水平,所以瑞神来请求你帮他计算出共有多少个位置会被"降智打击”。

Input

4
4 2 3 2

Output

39

思路

朴素的DFS，和BFS能拿到40分。据说剪枝后可以A掉，但是要注意考虑层数，（第4次和21次以同一方向道道某个点并不能剪掉），否则会WA。下面给出一种好的解法（这里感谢下hf大佬。

首先考虑分裂30次，$2^{30}$显然会TLE。考虑每次分裂是对称的，其实我们只需要考虑一半就行，如只考虑向右边分裂，把分裂后的图沿着对称轴对称过去，这样问题变成了30次图的对称复制。

至于怎么对称，考虑：

我们已知线段L，点A，求点A的对称点B。

那么问题就很简单了，高数学过（我却忘了，LY老师Dbq）：

• 对于上、下、左、右。很简单
• 对于其它方向，用下式推导，结果很好看。

总结

set用法
这题我算错复杂度了，以为朴素的dfs就能A。（问问自己，第几次这样了？？？）。然后玩了半小时（RNG NB）。最后看出来怎么做了，奈何不会算对称点，最后拿了暴力的40分，只能补题了。

代码

#include 
#include 
#include 
#include 
#include 
#include 
#include 
using namespace std;
struct re {
     
    int x, y;
    bool operator<(const re& a) const {
      return x != a.x ? x < a.x : y < a.y; }
};
set<re> M;
int ans;
int fx[] = {
     0, 1, 1, 1, 0, -1, -1, -1};
int fy[] = {
     1, 1, 0, -1, -1, -1, 0, 1};
int v[50], n;
void dfs(re cur, int k, int flag) {
     
    if (k > n) return;
    // cout << k << " " << flag << endl;
    dfs({
     cur.x + fx[flag] * v[k], cur.y + fy[flag] * v[k]}, k + 1, (flag + 1) % 8);
    set<re> temp;
    for (auto& i : M) {
     
        if (flag == 0 || flag == 4)
            temp.insert({
     cur.x * 2 - i.x, i.y});
        else if (flag == 1 || flag == 5)
            temp.insert({
     i.y + cur.x - cur.y, i.x - cur.x + cur.y});
        else if (flag == 2 || flag == 6)
            temp.insert({
     i.x, cur.y * 2 - i.y});
        else if (flag == 3 || flag == 7)
            temp.insert({
     cur.x + cur.y - i.y, cur.x + cur.y - i.x});
    }
    M.insert(temp.begin(), temp.end());
    for (int i = 1; i <= v[k]; i++) {
     
        M.insert({
     cur.x + fx[flag] * i, cur.y + fy[flag] * i});
    }
}
int main() {
     
    cin >> n;
    for (int i = 1; i <= n; i++) {
     
        cin >> v[i];
    }
    dfs({
     0, 0}, 1, 0);
    cout << M.size();
    return 0;
}