邓俊辉老师算法学习
文章目录
- 1 排序
- Gnome排序
- BubbleSort
- Huffman编码
- 2 贪心
- BST & BBST
- Hashtable
- 最小生成树 MST
- 3 decrease & conquer
- 概念
- 减而治之
- 选择排序
- 插入排序
- 选取 Quick Select
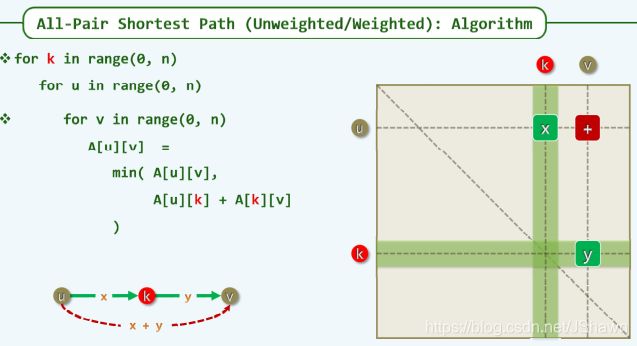
- 最短路径
- 4 divide and conquer
- 最大的和
- 乘法
- 归并排序
- Linear select
- 5 Graph Search
- BFS
- DFS
- 6 动态规划
- Fibnacci
- power
- LCS
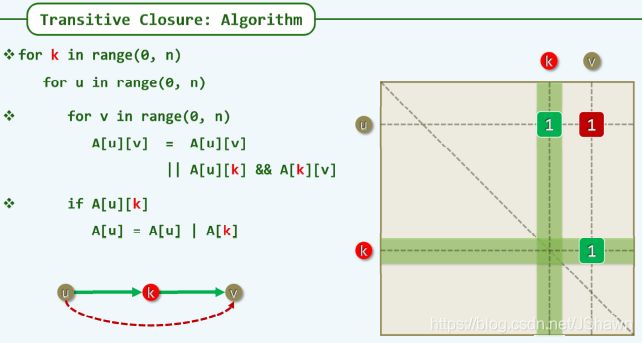
- 传递闭包
- 7 字符串
1 排序
Gnome排序
略去大括号
naiveGnomesort( s[],n)
for ( int i=1; i<n; ;)
if (i<1 || s[i-1]<= s[i])
i++;
else
swap( s[i-1],s[i] ); i--;
顺序则前进,遇逆序则折返,直到不再逆序或达到头部
效率较低:
若初始序列最开始完全逆序,需要进行 n(n+1)/2 次
稍作改进:
improvedGnomesort( s[],n)
for ( int =1; k<n; k++)
for (int i=k; 0<i && s[i-1]> s[i]; i--)
swap( s[i-1],s[i] );
BubbleSort
两两相邻的关键字,若反序则交换,直到没有反序的记录为止。
两层循环
for (i=0; i<n-1; i++) //从小到大排列
for (j=n-1; j >i ; j--) //每次循环将后续中最小的放到i位置
if (k[j-1] > k[j])
swap( k[i-1],k[i] );
也可以写成 (相当于从后向前排)
for (i=0; i<n-1; i++) //从小到大排列
for (j=1; j<n-i ; j++) //每次循环将后续中最大的放到n-i位置,即当前的最后一个
if (k[j-1] > k[j])
swap( k[i-1],k[i] );
在每次扫描交换时,已经完成部分排序,调过这部分,改进:
for (i=0; i<n-1; i++) //从小到大排列
for (j=1; j<n-i ; j++) //每次循环将后续中最大的放到n-i位置,即当前的最后一个
if (k[j-1] > k[j])
swap( k[i-1],k[i] );
last = j; //记录最后一个交换的位置
i=n-last; //再次扫描到last位置即可
demo:matrix sorting
一个矩阵先做列排序,再做行排序,证明列的结果依然有序。
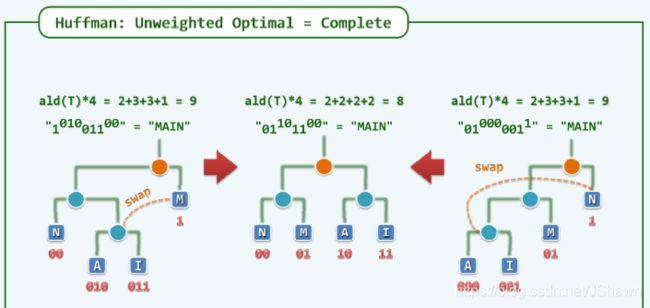
Huffman编码
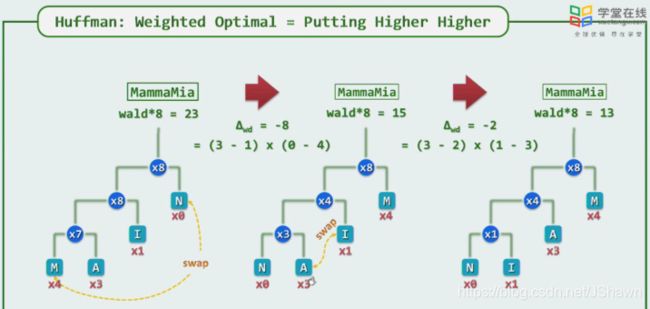
为了提高效率,通过交换不同结点,减小二叉树的深度差,使其较为平衡。
但实际的字母或中文出现频率可能不同,若仅考虑树的平衡,效率较低,可以将较高频的字母向上放置(贪心)。
可以用栈和队列结合,生成需要的二叉树
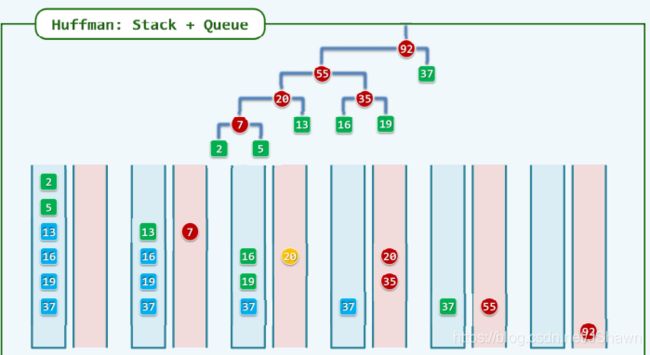
蓝色是栈,红色是队列。
①首先排序
②弹出栈顶两个,将它们的root放入到队列中
③栈顶和队首是最小的两个, pop & dequeue 生成结点放入队列中
④栈顶两个最小,pop并生成root -> inqueue
重复
每次操作次数是常数,总体为 O(n)
2 贪心
BST & BBST
BBST:平衡二叉树。 总体上提高查找效率
Hashtable
Python中 的字典利用的就是哈希表的数据结构。
散列表关键在于如何映射。
eg : hash(key)= key % M M通常取素数
Huffman若用顺序结构存储,每次迭代都需要遍历,运行效率较低, O(n.^2)
用三角形堆表示,再用get()等, O(nlogn)
最小生成树 MST
minium spanning tree
边的数量要适中,同时要考虑权重。
Prim方法,也是一种贪心思想,着眼于点,每次选取最短的路径/ 权重。
Kruskal方法,同为贪心思想,着眼于边,首先选出最短的边。
时间复杂度:
Prim:该算法的时间复杂度为O(n.^2)。与图中边数无关,该算法适合稠密图。
Kruskal:需要对图的边进行访问,所以克鲁斯卡尔算法的时间复杂度只和边有关,时间复杂度为O(nlogn),适合稀疏图。
3 decrease & conquer
概念
堆顶(根结点)是最大或最小
满二叉树的左孩子 LC(k)= ( k<<1)+1
<<表示左移一位,即 2k+1
满二叉树的右孩子 LC(k)= ( k+1) <<1 2k+2
插入和删除的时间复杂度为 O(logn)
减而治之
problem -> subproblem(n-1) + subproblem(1)
典型应用 -> binary search,复杂度为O(logn)
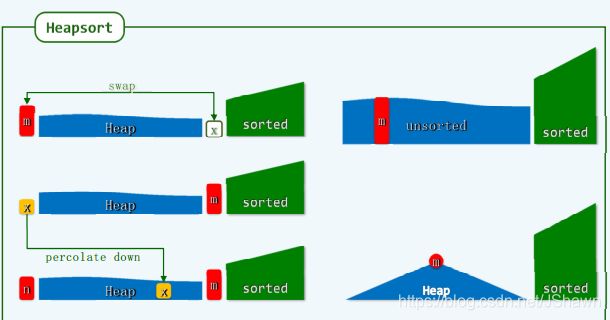
选择排序
基于减而治之的排序方法:选择排序 O(logn)
每次选出最大或最小放到末尾或开头,通过两两比较不断更新。
选择排序和冒泡排序区别:
选择排序的未完成部分顺序是随机的
对选择排序的改进:
用heap辅助,每次去掉堆顶,时间复杂度变为 O( nlogn)
插入排序
将未排序的部分向前插入,插入位置应该是唯一的。
(大部分人打牌的时候整理牌就是插入排序,如果打牌用选择排序,要等牌发完才能排序)
复杂度也是O( nlogn)
选取 Quick Select
若要选取第k大的元素,并不需要排序,可用一种随机的方法。
以扑克牌为例,随机pick一张,比它小的放到左边,大的放到右边,若运气好,比他小的正好k-1个,则完成,不是的话:

大了小了都可进一步减而治之,例如猜大了,则k位于绿色部分,猜小了则位于蓝色部分,可以去掉无用的部分。
最坏的情况不过是n次,优于先排序后选取。
最短路径
现实中很多时候需要选取最短路径或路费最低
Dijkstra算法:
以绳子串珠子来模拟,拉直起点与终点即可,思想很相似,不用考虑最后松弛的绳子。
每次从终点倒退回上一个点,这一点和起点之间的路径也必然最短。
无环的路径,可视作起于S的一棵树,图中的绿色线即为绷直的所有线,可到达图中任意点。
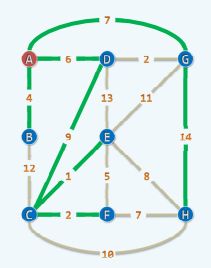
有时会出现负权值,这时新加入的与其负权值的结点需要进一步考虑,甚至可能有环路,此算法不解决负权值问题。



因此,用堆来实现较好。
堆的优点是始终维持一个最值,每次即对应下一个选取的点,此时在logn的时间内再次恢复堆。

4 divide and conquer
分而治之
problem (n) = subproblem (n/2) + subproblem (n/2)

最大的和
乘法
归并排序
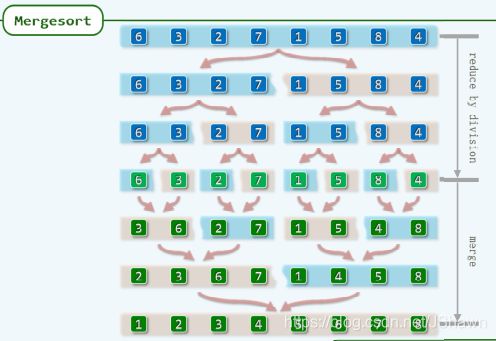
divide -> merge
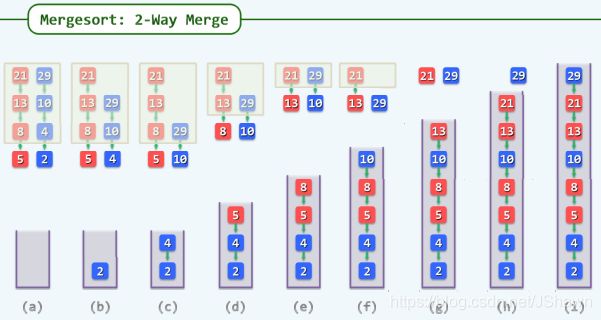
每次只针对队列前两个比较,merge T(n)=2T(n/2) +O(n)= O(nlogn)
逆序对通常记为 I inversion
一个元素前面有几个比它大,就认为有几对,第k个元素的逆序对 i(k) ,I=sum(i)
i(k)决定了对k排序时的成本,因此对于插入排序 O(n+I)
插入排序具有输入敏感性。
Linear select
①分成 Q 个序列
②对每段排序并得到每段的中位数
③找出Q个medians的median

5 Graph Search
BFS
Breadth-First-Search 广度优先遍历:是一种利用队列实现的搜索算法。
简单来说,其搜索过程和 “湖面丢进一块石头激起层层涟漪” 类似。
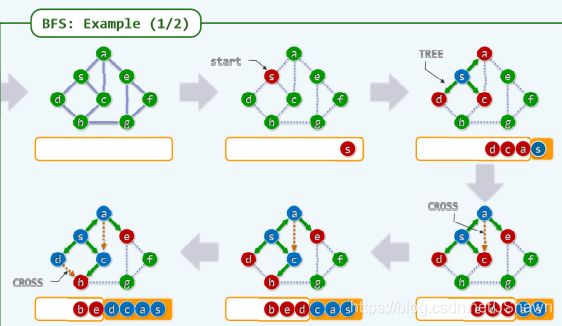
BFS可应用于最短路径问题
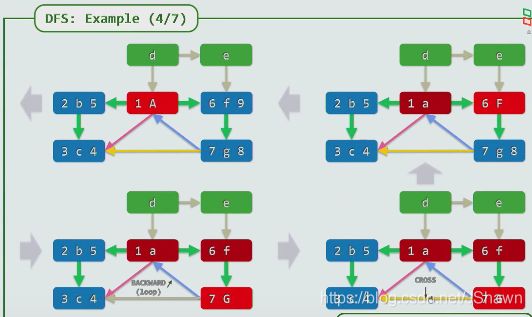
DFS
Depth-First-Search 深度优先遍历
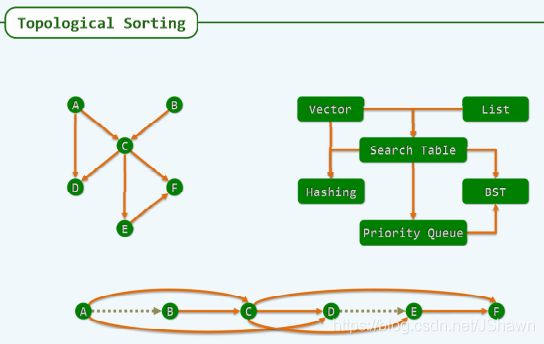
拓扑排序 demo:
课程的学习顺序,教师的写作顺序(不应有环路)
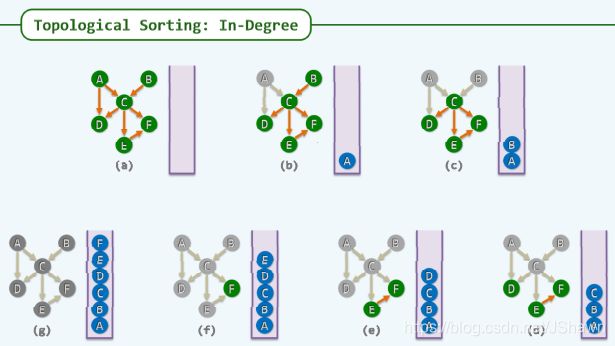
 从入度角度入手进行排序:
从入度角度入手进行排序:
①找到 0 入度(In-degree) 的点
②去掉①的点,继续找 0 入度的点
③不断重复,直到没有 0 入度的点
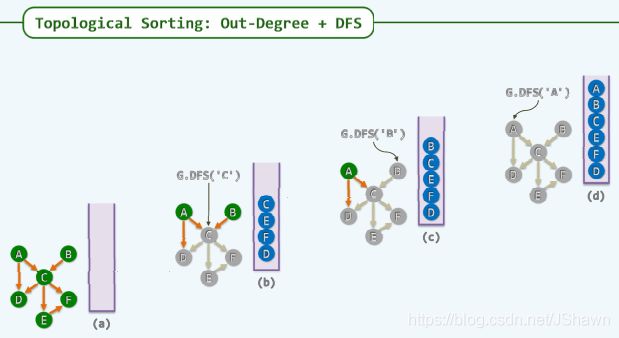
利用出度和DFS改进:
①随机选取起点(图中的D),利用DFS前进
②找到出度为 0 的点 (第一个开始回溯的)压栈
③将有backtrack的点依次压栈,直到再无回溯
④再次随机选取起点(图中的B),重复DFS
⑤栈中顺序记为可行的学习顺序(A,B可交换)
BFS 常用于找单一的最短路线,它的特点是 “搜到就是最优解”,而 DFS 用于找所有解的问题,它的空间效率高,而且找到的不一定是最优解,必须记录并完成整个搜索,故一般情况下,深搜需要非常高效的剪枝。
6 动态规划
Fibnacci
用递归法计算斐波那契数列第n项的时间复杂度本身也是斐波那契数列。
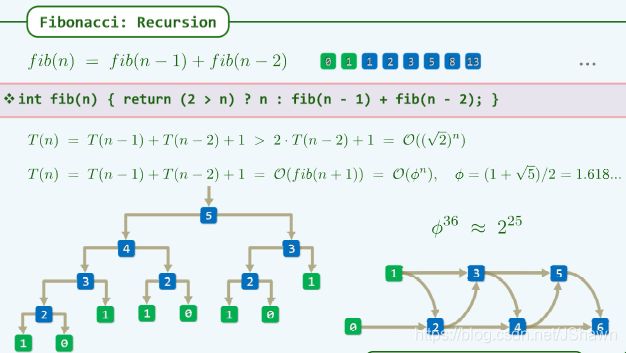
用记忆化方法改进 memoization
用一个状态量,如 defined undefined区分是否已计算,避免大量重复递归运算。
(建立一个lookuptable)

power
指数利用动态规划,可以变为 O(logn) 复杂度

斐波那契数列的运算可以转化为矩阵运算(图右)
那么第n项可以用 logn 时间运算完成,但实际操作存在困难

demo:
柜台结账,每个有固定等候时间,算出每个口的等候时间,用主动向后计算代替向前递归查找(左)
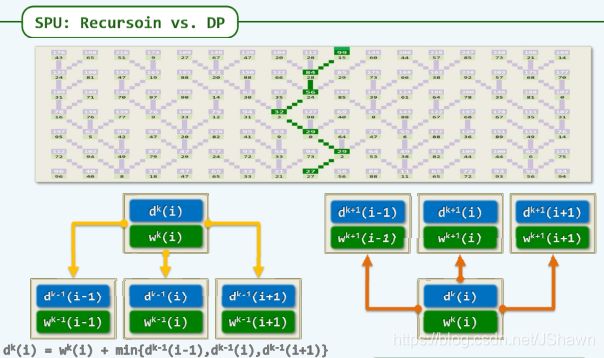
demo: 最长曼哈顿道路

从左上到右下,而非从终点到起点的回溯。
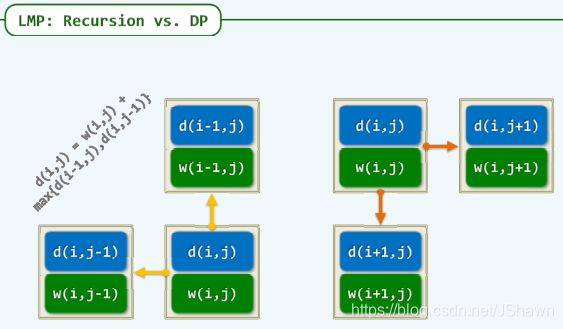
LCS
longest common subsequence 最长公共子序列