压缩感知重构算法之正交匹配追踪(omp)及其matlab实现
压缩感知之OMP恢复算法
1、基本思想
y=Φx x=Ψθ
正交匹配追踪算法的本质思想是,以贪婪迭代的方式选择测量矩阵Φ的列,使得在每次迭代中所选择的列与当前的冗余向量最大程度地相关,从测量向量中减去相关部分并反复迭代,直到迭代次数达到稀疏度K,强制迭代停止。
2、算法步骤
输入:(1)M*N的感知矩阵A,其中M远远小于N,A=Φ*Ψ。
(2)长度为M的数据向量b,即测量值y。
输出:长度为N的重建向量xˆ,满足y=Ax。
初始化:残差r0=y,重建信号x0=0,索引集Λ0=Φ,迭代次数n=2*K,计数器k=0。
步骤1:计算残差和感知矩阵A的每一列的投影系数(内积值)ck=ATrk−1
步骤2:找出ck中元素最大的元素c∗k=max{ck}以及对应的位置pos;
步骤3:更新索引集 Λk=Λk−1∪{pos},以及原子集合AΛK=AΛk−1∪{A(:pos)} ;
步骤4:利用最小二乘求得近似解 xk=(ATΛkAΛk−1)−1ATΛky
步骤5:更新余量rk=y−Axk ;
步骤6:判断迭代是否满足停止条件,满足则停止xˆ=xk,r=rk, 输出xˆ,r ,否则转步骤1。
3、仿真验证
3.1 一维时间稀疏信号
首先进行一维时间稀疏信号的恢复,信号长度为512,稀疏度选取10、20、30、40、50,matlab代码如下:
clc;clear;close all
%% 1. 时域测试信号生成
CNT = 100; %对于每组(K,M,N),重复迭代次数
N=512; %信号长度
K_set= [10,20,30,40,50]; %信号x的稀疏度集合
Percentage = zeros(length(K_set),N); %存储恢复成功概率
for kk=1:length(K_set)
K=K_set(kk); %本次稀疏度
M_set=1:5:N; %测量数每隔五个取一次
PercentageK = zeros(1,length(M_set)); %存储此稀疏度K下不同M的恢复成功概率
for mm=1:length(M_set)
M=M_set(mm); %本次观测次数
P=0;
for cnt=1:CNT %每个观测值个数均运行CNT次
Index_K=randperm(N); %将1-N随机打乱 行向量
x=zeros(N,1);
x(Index_K(1:K))=5*randn(K,1); %x为K稀疏的,且位置是随机的
%% 2. 时域信号压缩传感
Phi=randn(M,N); % 测量矩阵(高斯分布白噪声)
Phi = Phi./repmat(sqrt(sum(Phi.^2,1)),[floor(M),1]); %正则化
y=Phi*x; % 获得线性测量
%% 3. 正交匹配追踪法重构信号(本质上是L_1范数最优化问题)
n=2*K; % 算法迭代次数(m>=K)
Psi=eye(N); % 单位矩阵为正变换矩阵
A=Phi*Psi; % 恢复矩阵(测量矩阵*正交反变换矩阵)
hat_y=zeros(1,N); % 待重构的变换域里的向量
Aug_t=[]; % 增量矩阵(初始值为空矩阵)
r0=y; % 残差值
for times=1:n; % 迭代次数(有噪声的情况下,该迭代次数为K)
for col=1:N; % 恢复矩阵的所有列向量 步骤1
product(col)=abs(A(:,col)'*r0); % 恢复矩阵的列向量和残差的投影系数(内积值)
end
[val,pos]=max(product); % 最大投影系数对应的位置 步骤2
Aug_t=[Aug_t,A(:,pos)]; % 矩阵扩充 步骤3 更新原子集合
A(:,pos)=zeros(M,1); % 选中的列置零(实质上应该去掉,为了简单我把它置零)
aug_y=(Aug_t'*Aug_t)^(-1)*Aug_t'*y; % 最小二乘,使残差最小 步骤4 求近似解
r0=y-Aug_t*aug_y; % 残差 步骤5 更新余量
pos_array(times)=pos; % 纪录最大投影系数的位置 步骤3 更新索引集
end
hat_y(pos_array)=aug_y; % 重构的变换域里的向量
hat_x=real(Psi'*hat_y.'); % 做逆变换重构得到时域信号
if norm(hat_x-x)<1e-6 %如果残差小于1e-6则认为恢复成功
P = P + 1;
end
end
PercentageK(mm) = P/CNT; %计算恢复概率
end
Percentage(kk,1:length(M_set)) = PercentageK;
end
save MtoPercentage100 %运行一次不容易,把变量全部存储下来
%}
%% 绘制概率图
S = ['-ks';'-ko';'-kd';'-kv';'-k*'];
figure;
for kk = 1:length(K_set)
K = K_set(kk);
M_set = 1:5:N;
L_Mset = length(M_set);
plot(M_set,Percentage(kk,1:L_Mset),S(kk,:));%绘出x的恢复信号
hold on;
end
hold off;
xlim([0 256]);
legend('K=10','K=20','K=30','K=40','K=50');
xlabel('Number of measurements(M)');
ylabel('Percentage recovered');
title('Percentage of input signals recovered correctly(N=256)(Gaussian)');
%% 4. 恢复信号和原始信号对比
% figure(1);
% hold on;
% plot(hat_x,'k.-') % 重建信号
% plot(x,'r') % 原始信号
% legend('Recovery','Original')
% norm(hat_x.'-x)/norm(x) % 重构误差程序代码改变测量数得到恢复概率,如下图所示
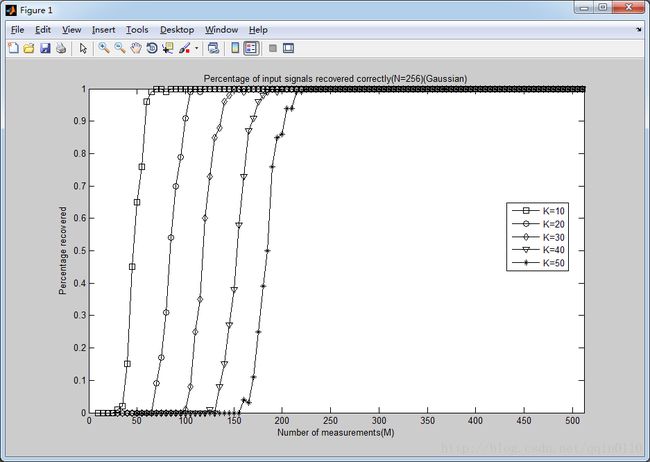
《压缩感知及应用》书上的p68页图3-7如下 
结果要比《压缩感知及应用》书上p68页结果感觉略好,原因不详。
3.2 二维lena图像恢复
仿照《压缩感知及应用》这本书,p120页,进行lena图像恢复,压缩比使用0.3、0.4、0.5。所程序如下:
img=imread('lena256.bmp'); %读文件
img=double(img);
[n,b]=size(img); %文件为n行b列
figure(1)
subplot(2,2,1)
imshow(img,[])
weizhi=1;
Pm=zeros(3,1); %放功率信噪比
Tm=zeros(3,1); %放时间
for CR=0.3:0.1:0.5
disp(CR);
% 测量矩阵
m=floor(n*CR);
Phi=randn(m,n); % 测量矩阵生成
for i=1:n % 测量矩阵归一化
Phi(:,i) = Phi(:,i) / norm(Phi(:,i));%正则化测量矩阵φ
end
% 对图像进行欠采样
y=Phi*img;
%% CS重建( 已知测量值y,测量矩阵Phi,稀疏基Psi'(小波变换矩阵) )
Psi=DWT(n); % 小波变换矩阵生成(要求大小是2的整数幂次)%傅里叶正变换矩阵dftmtx(n)
A = Phi*Psi'; % y = Phi*X0 = Phi*Psi'*s(s是稀疏系数)此处X0=Psi's
y = y*Psi'; % 此处不明白,为什么还要乘psi' 如果不乘,恢复效果很差
%OMP算法
tic
fprintf('OMP...\r\n');
ReS3 = zeros(n,b);
for i = 1:b
rec = omp(y(:,i),A,n); %对y的的每一列进行重构,恢复变换域矩阵
ReS3(:,i) = rec;
end
T3 = toc;
ReS3 = Psi'*sparse(ReS3)*Psi; %%%%%%%%%%%%%%%
ReImg3 = full(ReS3);
weizhi=weizhi+1;
subplot(2,2,weizhi)
imshow(ReImg3,[]);
%% 计算峰值噪声(PSNR)、用时
% OMP
errorx=sum(sum(abs(ReImg3-img).^2)); % MSE误差
psnr=10*log10(255*255/(errorx/n/b));%
Pm(weizhi-1,1)=psnr;
Tm(weizhi-1,1)=T3;
end
%% 显示结果
CR=0.3:0.1:0.5;
figure;
plot(CR,Pm(:,1),'ro');
hold on
plot(CR,Pm(:,1),'r');
xlabel('压缩比');
ylabel('峰值信噪比/dB');
axis([0.2,0.6,5,30]);
figure;
plot(CR,Tm(:,1),'g*')
hold on
plot(CR,Tm(:,1),'g')
xlabel('压缩比');
ylabel('运行时间/s');
axis([0.2,0.6,0,1+max(Tm(3,:))]);
function hat_y=omp(s,T,N)
% OMP的函数
% s-测量;T-观测矩阵;N-向量大小
Size=size(T); % 观测矩阵大小
M=Size(1); % 测量
hat_y=zeros(1,N); % 待重构的谱域(变换域)向量
Aug_t=[]; % 增量矩阵(初始值为空矩阵)
r_n=s; % 残差值
for times=1:M; % 迭代次数(不会超过测量值)
for col=1:N; % 恢复矩阵的所有列向量
product(col)=abs(T(:,col)'*r_n); % 恢复矩阵的列向量和残差的投影系数(内积值)
end
[val,pos]=max(product); % 最大投影系数对应的位置
Aug_t=[Aug_t,T(:,pos)]; % 矩阵扩充
T(:,pos)=zeros(M,1); % 选中的列置零(实质上应该去掉,为了简单我把它置零)
aug_y=(Aug_t'*Aug_t)^(-1)*Aug_t'*s; % 最小二乘,使残差最小
r_n=s-Aug_t*aug_y; % 残差
pos_array(times)=pos; % 纪录最大投影系数的位置
if (abs(aug_y(end))^2/norm(aug_y)<0.0005) % 自适应截断误差(***需要调整经验值)
break;
end
end
hat_y(pos_array)=aug_y; % 重构的向量
% 程序作者:沙威,香港大学电气电子工程学系,[email protected]
% 参考文献:小波分析理论与MATLAB R2007实现,葛哲学,沙威,第20章 小波变换在矩阵方程求解中的应用(沙威、陈明生编写).
% 构造正交小波变换矩阵,图像大小N*N,N=2^P,P是整数。
function ww=DWT(N)
[h,g]= wfilters('sym8','d'); % 获得symlets8小波的低通分解滤波器和高通分解滤波器的系数;
% 采用Symlets8的小波分解可得到较好的压缩比率及较高的信号恢复质量
% N=256; % 矩阵维数(大小为2的整数幂次)
L=length(h); % 滤波器长度
rank_max=log2(N); % 最大层数 8 ?
rank_min=double(int8(log2(L)))+1; % 最小层数 5 ?
ww=1; % 预处理矩阵
% 矩阵构造
for jj=rank_min:rank_max
nn=2^jj;
% 构造向量
p1_0=sparse([h,zeros(1,nn-L)]);
p2_0=sparse([g,zeros(1,nn-L)]);
% 向量圆周移位
for ii=1:nn/2
p1(ii,:)=circshift(p1_0',2*(ii-1))'; %对1*m矩阵来说,相当于右移
p2(ii,:)=circshift(p2_0',2*(ii-1))';
end
% 构造正交矩阵
w1=[p1;p2];
mm=2^rank_max-length(w1);
w=sparse([w1,zeros(length(w1),mm);zeros(mm,length(w1)),eye(mm,mm)]);
ww=ww*w; % ?
clear p1;clear p2;
end结果如下,第一幅为原图,然后依次为压缩比0.3、0.4、0.5, 
psnr和所用时间分别如下 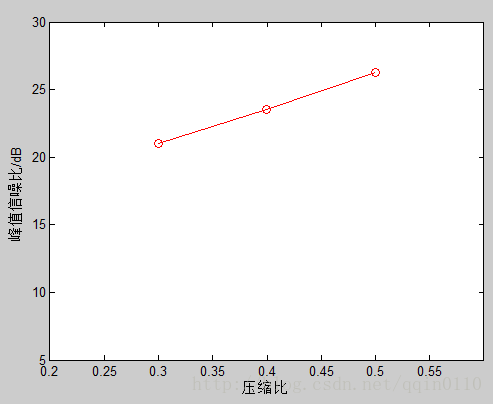

书上的图像如下,依次为原图,压缩比为0.5、0.4、0.3 
所得实际结果感觉较之稍差。
4、结果分析
由于使用的测量矩阵为高斯随机矩阵, 所以每次结果会有偏差,这是部分原因,其余应该还有其它原因。
5、参考文献
1、《压缩感知及应用》,闫敬文 刘蕾 屈小波
2、沙威老师压缩感知代码
3、彬彬有礼的博客,地址如下
http://blog.csdn.net/jbb0523/article/details/45130793