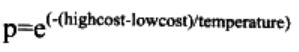读书笔记:“集体智慧编程”之第五章:“求最优解”的算法
优化
显然刚开始我并不太明白这一章要讲什么,因为根据“优化”这个词,我还以为是对函数进行优化之类的。后来,我才明白,这一章在要讲求最最优解的算法。由于我曾在老师的算法课上讲过遗传算法,遗传算法就是用来求最优解的算法,所以我忽然明白了这个优化具体是指什么。
制定旅行计划的例子
情况描述
当然本次旅游也不是说你想怎么样就怎么样的,有很多限制条件,在这些限制条件之下,怎么安排这次计划,具体来说,就每个人出行的时间、乘坐航班的时间、是否转机、租用车辆的时间。综合来说,我们并不是要某一个人感到他自己方便了,而是要所有的人在相互磨合之下,所有人都方便了,并且要保证成本消耗最低,比如机票的价格不同吧?比如租车时间的长短,这是因为租车要花钱吧。显然这一段是一个抽象的描述,下面,我们来看看如何具体到底有什么要求?注意,会非常具体,具体到每一个航班的始发时间和价格。
准备工作
首先,要明白是六个人(亲戚吧),他们本来分散在美国的全国各地,然后呢?他们约好了某一天,一起到纽约旅游,本地约定一天往返,他们就旅游这么一天。所以,我们可以写出如下代码:
#将要去旅行的人,第一个是名字,第二个是目前所在地
people = [('Seymour','BOS'),
('Franny','DAL'),
('Zooey','CAK'),
('Walt','MIA'),
('Buddy','ORD'),
('Les','OMA')]
#他们都要到美国的纽约集合,这是旅行的目的地
#LGA是纽约的机场
destination = 'LGA'从他们所在地到纽约是乘坐飞机,但是飞机有不同的航班,航班的价格也不一样。书中为我们准备了一份航班列表:schedule.txt,供我们使用,我节选其中一部分进行讲解,如下所示
LGA,OMA,18:25,20:34,205
OMA,LGA,18:12,20:17,242
我们必然会在代码中会使用这些航班信息,因为我们要针对每一个人,选出一对航班,让他从当前位置飞到纽约,再从纽约飞回他的家。所以,先让我们把这份文件读进代码,我们决定放在一个字典内,再次强调,字典就是键值对。
其中setdefault的函数,比较难理解,可以 参考这里
代码如下:
#我们将所有的航班信息读到一个字典内,以起止点为键,其他的为值
flights={}
for line in file('schedule.txt'):
origin,dest,depart,arrive,price = line.strip().split(',')
#其中setdefault是作为字典类的一个方法,主要的作用是应对一种情况:当一个键对应多个值,每一个值是一个元组,多个元祖组成一个列表,
#说白了,一个键对应一个列表,列表内有许多的元祖,一个元祖代表一个航班信息
#setdefault的含义是:"如果没有,就设置",如果有,就添加。
flights.setdefault((origin,dest),[])
#现在我们一行一行的把航班信息加入进去
#我认为,我们是对一个列表作为值,所以最外面是一个[]
#里面跟了一个元祖,这个元祖就是键
flights[(origin,dest)].append((depart,arrive,int(price)))
#通过print flight,我们可以看出在该字典中具体的存储情况。一个起止点作为一个值,对应了一个列表,而列表中有许多元祖,每一个元祖都是一个航班信息的起飞时间、降落时间和价格此时,我们需要加入一个函数,函数是将几点几分,转换为从凌晨0点开始经过了多少分钟,需要这个函数的原因:几点几分的比较非常不便,而单纯的分钟数,使得飞机的飞行时间、候机时间变得容易计算。
代码:
def getminutes(t):
#strptime是将特定的时间格式转化为元组。
x=time.strptime(t,'%H:%M')
return x[3]*60+x[4]
#我觉得x[0]x[1]x[2]是年月日下面我们要规定一种方式,用这种方式用来简单的表达某一个人选择了哪两个航班。实际上这就是我们的解,我们求的最优解,就是用这种方式来表达。从书中读到,我们要注意对类似的问题、类似的解做到通用,显然这个思维非常重要,但是目前对我来说,缺少太多实践经验,所以不容易。在题本中,我们用一组数组数列来表示,数组在python里面叫做列表。如下所示:
[1,4,3,2,7,3,6,3,2,4,5,3]
显然,如果我们每次都这么读这一串数字是非常辛苦的,所以我们决定写一个函数,这个函数接受这一串数字列表,然后将人名、和起飞时间,起飞地点等信息都完整的打印出来。
代码:
def printschedule(r):
for d in range(len(r)/2):#针对每一个人打印两个航班信息,我们只用重复r的一半次
name=people[d][0]
origin= people[d][1]
out=flights[(origin,destination)][r[2*d]]
ret=flights[(destination,origin)][r[2*d+1]]
print '%10s%10s %5s-%5s $%3s %5s-%5s $%3s' % (name,origin,out[0],out[1],out[2],ret[0],ret[1],ret[2])我上面这段代码改错改了很久,主要就是少了符号":"还有就是少了'’的s。
成本函数
下面我们要做一个函数,叫做成本函数。顾名思义,就是我们做一件事的成本和代价。该函数有一个输入:就是航班信息,有一个输出,就是一个数字,数字越大代表代价越高。
书中提到:成本函数是用最优化算法的关键,这是因为它往往难以确定,到底哪些是成本,成本的大小有多少?通过这个例子我相信大家有着更深刻的体会。下面请一个一个看,有哪些成本和这些成本如何用金钱来度量。
- 飞机的价格:6个人乘坐12次飞机的机票费用,显然我们希望价格越低越好。价格的金钱度量很直接。
- 飞行时间:每个人在乘坐飞机时所花费的时间,我们当然希望乘坐飞机的时间越短越好。每分钟1美元。(代码中忽略了)
- 等待时间:在机场等待其他成员到达的时间,当然我们希望这个时间越短越好。每分钟1美元。
- 出发时间:早晨太早的飞机将会产生额外的成本,该成本就是要求旅游的人减少睡眠时间。我们希望尽可能的不要早,要合适。所以这个数字应该是越晚越好。(代码中忽略了)
- 汽车租用时间:集体租用一辆车,那么因为只旅游一天而已,所以租车的时间最好要控制在二十四小时之内。超过之后会产生额外的成本。超过二十四小时则产生50美元的罚款。
上述这是书中作者找到的关键的成本因素和金额度量。我们按照自己觉得合理的方式随意改动。
代码如下:
def schedulecost(sol):
totalprice=0
latestarrival=0#最晚到底时间
earliestdep=24*60#最早离开时间,现在24*60是最好的情况,等一下会根据实际飞机情况发生改变
for d in range(len(sol)/2):
#得到每一个人的两次航班的价格并且加入到总价格中
origin = people[d][1]
outbound = flights[(origin,destination)][int(sol[2*d])]
returnf = flights[(destination,origin)][int(sol[2*d+1])]
#把钱加入到总价格里面去
totalprice+=outbound[2]
totalprice+=returnf[2]
#根据实际情况改变最晚到达时间和最早离开时间
if latestarrivalgetminutes(returnf[0]):earliestdep=getminutes(returnf[0])
#每一个人必须在机场等待直到最后一个来了才能出发
#每一个人必须在旅游结束时,为了最早离开的人能够赶上飞机,而来到机场等候
totalwait=0
for d in range(len(sol)/2):
origin = people[d][1]
outbound = flights[(origin,destination)][int(sol[2*d])]
returnf = flights[(destination,origin)][int(sol[2*d+1])]
totalwait+=latestarrival-getminutes(outbound[1])
totalwait+=earliestdep-getminutes(returnf[0])
if latestarrival 现在我成功打印出成本了,现在目标就是找出正确的数字序列,使成本最低。根据书中解释,一共是12次航班,每次有10种不同的航班。那么可以得到10的12次方个组合,就大约1000亿。如果我们将这1000亿个逐一比较,肯定能找到最佳答案。但是在计算机上耗费的时间很长。
随机搜索
所以我们需要求最优解。在正在开始学习最优化算法之前,让我们先来学一个叫随机搜索的东西。
随机搜索不是最优化算法,但是我们用它来评估其他算法的优劣。实际上,他就是随机产生结果。但是我们可以重复随机产生一堆结果...用来干什么我就不知道了。下面我们直接看代码吧,关键的部分我会在相应出解释。
代码:
#domain代表随机产生的数字的个数和每一个数字的范围,是一个列表,列表里每个元素里面是一个元组,每个元组有2个元素,一个是上限,一个是下限
#costf就是成本函数,
#每次随机产生一组结果的时候,我们将会使用costf进行一下测试,看看效果如何
def randomptimize(domain,costf):
best=999999999
bestr=None
for i in range(10000):#我们打算随机产生1000次结果,从这1000次结果中选择一个最好的
#很显然randint是产生在一定范围内的随机数,显然由于下一句右边等号里的for,将会产生一个循环
r=[random.randint(domain[i][0],domain[i][1])for i in range (len(domain))]
cost=costf(r)
#每次得到成本我们都判断一次,如果更低,我们就置换
if cost其中对domain这个理解需要比较到位,如下产生,打印出来看看就明白是什么了
>>> domain=[(0,9)]*(len(people)*2)
>>> print domain
[(0, 9), (0, 9), (0, 9), (0, 9), (0, 9), (0, 9), (0, 9), (0, 9), (0, 9), (0, 9),
(0, 9), (0, 9)]爬山法
核心思维
经过查看flights{}字典发现,原来每一个键都是按照时间顺序排列的
>>>
{('LGA', 'CAK'): [('6:58', '9:01', 238), ('8:19', '11:16', 122), ('9:58', '12:56', 249), ('10:32', '13:16', 139), ('12:01', '13:41', 267), ('13:37', '15:33', 142), ('15:50', '18:45', 243), ('16:33', '18:15', 253), ('18:17', '21:04', 259), ('19:46', '21:45', 214)], ('DAL', 'LGA'): [('6:12', '10:22', 230), ('7:53', '11:37', 433), ('9:08', '12:12', 364), ('10:30', '14:57', 290), ('12:19', '15:25', 342), ('13:54', '18:02', 294), ('15:44', '18:55', 382), ('16:52', '20:48', 448), ('18:26', '21:29', 464), ('20:07', '23:27', 473)], ('LGA', 'BOS'): [('6:39', '8:09', 86), ('8:23', '10:28', 149), ('9:58', '11:18', 130), ('10:33', '12:03', 74), ('12:08', '14:05', 142), ('13:39', '15:30', 74), ('15:25', '16:58', 62), ('17:03', '18:03', 103), ('18:24', '20:49', 124), ('19:58', '21:23', 142)], ('LGA', 'MIA'): [('6:33', '9:14', 172), ('8:23', '11:07', 143), ('9:25', '12:46', 295), ('11:08', '14:38', 262), ('12:37', '15:05', 170), ('14:08', '16:09', 232), ('15:23', '18:49', 150), ('16:50', '19:26', 304), ('18:07', '21:30', 355), ('20:27', '23:42', 169)], ('LGA', 'OMA'): [('6:19', '8:13', 239), ('8:04', '10:59', 136), ('9:31', '11:43', 210), ('11:07', '13:24', 171), ('12:31', '14:02', 234), ('14:05', '15:47', 226), ('15:07', '17:21', 129), ('16:35', '18:56', 144), ('18:25', '20:34', 205), ('20:05', '21:44', 172)], ('OMA', 'LGA'): [('6:11', '8:31', 249), ('7:39', '10:24', 219), ('9:15', '12:03', 99), ('11:08', '13:07', 175), ('12:18', '14:56', 172), ('13:37', '15:08', 250), ('15:03', '16:42', 135), ('16:51', '19:09', 147), ('18:12', '20:17', 242), ('20:05', '22:06', 261)], ('CAK', 'LGA'): [('6:08', '8:06', 224), ('8:27', '10:45', 139), ('9:15', '12:14', 247), ('10:53', '13:36', 189), ('12:08', '14:59', 149), ('13:40', '15:38', 137), ('15:23', '17:25', 232), ('17:08', '19:08', 262), ('18:35', '20:28', 204), ('20:30', '23:11', 114)], ('LGA', 'DAL'): [('6:09', '9:49', 414), ('7:57', '11:15', 347), ('9:49', '13:51', 229), ('10:51', '14:16', 256), ('12:20', '16:34', 500), ('14:20', '17:32', 332), ('15:49', '20:10', 497), ('17:14', '20:59', 277), ('18:44', '22:42', 351), ('19:57', '23:15', 512)], ('LGA', 'ORD'): [('6:03', '8:43', 219), ('7:50', '10:08', 164), ('9:11', '10:42', 172), ('10:33', '13:11', 132), ('12:08', '14:47', 231), ('14:19', '17:09', 190), ('15:04', '17:23', 189), ('17:06', '20:00', 95), ('18:33', '20:22', 143), ('19:32', '21:25', 160)], ('ORD', 'LGA'): [('6:05', '8:32', 174), ('8:25', '10:34', 157), ('9:42', '11:32', 169), ('11:01', '12:39', 260), ('12:44', '14:17', 134), ('14:22', '16:32', 126), ('15:58', '18:40', 173), ('16:43', '19:00', 246), ('18:48', '21:45', 246), ('19:50', '22:24', 269)], ('MIA', 'LGA'): [('6:25', '9:30', 335), ('7:34', '9:40', 324), ('9:15', '12:29', 225), ('11:28', '14:40', 248), ('12:05', '15:30', 330), ('14:01', '17:24', 338), ('15:34', '18:11', 326), ('17:07', '20:04', 291), ('18:23', '21:35', 134), ('19:53', '22:21', 173)], ('BOS', 'LGA'): [('6:17', '8:26', 89), ('8:04', '10:11', 95), ('9:45', '11:50', 172), ('11:16', '13:29', 83), ('12:34', '15:02', 109), ('13:40', '15:37', 138), ('15:27', '17:18', 151), ('17:11', '18:30', 108), ('18:34', '19:36', 136), ('20:17', '22:22', 102)]}
>>> 代码
核心思维结束了,让我们直接来看代码吧
def hillclimb(domain,costf):
#先创建一个随机的解
sol=[random.randint(domain[i][0],domain[i][1])for i in range (len(domain))]
while 1:#持续一个循环,直到在一次对每一个解减一或者加一之后没有任何改变时,就break
neighbors=[]
for j in range(len(domain)):
#解中的每一个元素都都会加一或者减一,加一产生一个解集,减一产生一个解集
if sol[j]>domain[j][0]:
#如果很熟悉
neighbors.append(sol[0:j]+[sol[j]-1]+sol[j+1:])
if sol[j]可以调用如下语句直接产生一个由爬山法制作出来的结果,当然请保证其他函数的存在。
domain=[(0,9)]*(len(people)*2)
sol=hillclimb(domain,schedulecost)
printschedule(sol)
print schedulecost(sol)
难点
其中有一个难点:sol[0:j]+[sol[j]-1]+sol[j+1:]
我做了个测试,看测试的还很清楚就能明白这个什么东西,加三个列表加起来,我觉得这个方法有点叼哇。最后一个错误请记住,要将三个列表相加的话,不要企图用数字。>>> sol=[1,4,3,2,7,3,6,3,2,4,5,3]
>>> a=[]
>>> a.append(sol[0:0]+[sol[0]-1]+sol[1:])
>>> print a
[[0, 4, 3, 2, 7, 3, 6, 3, 2, 4, 5, 3]]
>>> a.append(sol[0:0]+sol[0]-1+sol[1:])
Traceback (most recent call last):
File "", line 1, in
TypeError: can only concatenate list (not "int") to list
>>> 缺点
下面谈一下爬山法的缺点。我认为书本上的一幅图,非常好体现了爬山法缺点。简单来讲,爬山法只能找到局部最优解,不能找到全局最优解,而我们要找的当然就是全局最优解。当然我们可以重复使用爬山法,都使用不同的初始状态。
模拟退火算法
原理
为什么刚开始的概率大呢?因为温度高,所以指数接近了0,所以概率几乎为1,随着温度的减少,高成本与低成本之间的差值将会越来越重要,差异越大,概率越低。这注定了:该算法只会接受稍稍高一点成本的解,而不会接受成本高出许许多多的解。
代码
具体执行代码如下:
def annealingoptimize(domain,costf,T=10000.0,cool=0.98,step=1):
#和爬山法一样,先产生一个随机解,然后一切的改变都从这个随机解开始
vec=[random.randint(domain[i][0],domain[i][1])for i in range (len(domain))]
while T>0.5:
#产生一个随机数,决定这次改变是改变数列中的哪一个随机数
i=random.randint(0,len(domain)-1)
#选择一个改变的方向,也就是说是增加还是减少
dir=random.randint(-step,step)
#复制随机解,然后对随机解进行改变,然后判断到底新的解好,还是后来产生的解好
vecb=vec[:]
vecb[i]+=dir
#这一段主要还是不让它超不过了最大最小值的限制
if vecb[i]domain[i][1]:vecb[i]=domain[i][1]
#计算新产生的两次解的成本,然后对成本进行比较
ea=costf(vec)
eb=costf(vecb)
#or后面:表示接受更差的结果。仔细想想,原来概率的表示是如此完成的,注意前一个random()产生的数是在0到1之间。
if(eb 使用一下代码可以执行一次:
domain=[(0,9)]*(len(people)*2)
sol=annealingoptimize(domain,schedulecost)
printschedule(sol)
print schedulecost(sol)
经过我的验证,确实可以产生更不错的低成本,另外,偶尔也会得到一个较高成本的结果,记住一定要使用不同的参数多试一试。初始温度,冷却率,step的值等等。
遗传算法
原理
如下图
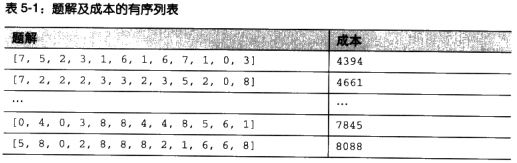
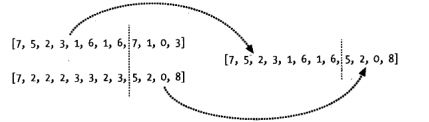
依据这个排了序的结果,我们将会产生下一个子代。为了使下一个子代的成本更低,我们首先选出目前这一代的优良品种,由于排序,很容易选择前几名,我们可以也约定好,选择前多少名。
变异的做法就是指对一个解里面某一个小部分进行小的改变,如下图所示。6改为5,0改成1,当然这肯定是有实际含义的对吧。
配对又称交叉,我们将两个优良品种各取一部分,组成一个新的解。当然,实际上,要根据实际情况的不同而进行调整。如下图所示:
代码
具体代码如下:
#popsize:一个种群的规模大小
#mutprob:种群中进行变异,而不进行配对的概率。
#elite:在当前种群中被认为优秀的子代的比例,优秀的子代可以直接传入下一代
#maxiter:迭代运行多少代
def geneticoptimize(domain,costf,popsize=50,step=1,mutprob=0.2,elite=0.2,maxiter=100):
#方法中还在定义方法
#变异操作
def mutate(vec):
i=random.randint(0,len(domain)-1)
#完成第增加或减少的概率各一半
if random.random()<0.5 and vec[i]>domain[i][0]:
return vec[0:i]+[vec[i]-step]+vec[i+1:]
elif vec[i]使用以下代码可以打印个结果:
domain=[(0,9)]*(len(people)*2)
sol=geneticoptimize(domain,schedulecost)
printschedule(sol)
print schedulecost(sol)总结
到了这里算是一个阶段性结束。我们主要对一个模型抽象出了数字列表,然后对 随机搜索、 模拟退火算法、 遗传算法进行了初步的理解和实现。我们发现在这里一系列问题中最困难的一步就是能否把问题潜在的解转化为数字列表。然后我个人觉得将整个问题转换为数字列表,或者能够运用编程的方式来解决就是很困难的。此外,上述的求最优解的方法能发挥的功效呢?和问题本身有着密切的联系。上述求最优解的方法都依赖于一个事实:最优解应该接近去其他优解。然而,显示中可能存在这里的问题,如下图所示:

可以看出最优解的左右两边是否得陡峭,当产生了接近于最优解的解,我会认为其不是优解而排除,最后我们只能陷入了局部最优解之中,上图的左方。
如果放在航班例子中来看,就是我们如果从当天的第二次航班转到第三次航班时,比将其转到第八次航班更有可能降低成本。这是因为航班有序排列,对每一个解集的一个航班加一或者减一效果肯定比减5、加6来的效果好。但是如果航班处于无序状态,我们的求最优解的方式则不会有太大的作用,还不如随机搜索。其中的航班处于无序状态。什么意思?起飞的航班必须有序呀。
书中下面一节将了通过真实的航班搜索来完成,这个单独开一篇博客,因为情况涉及调用外部api。会稍稍复杂一些。
有偏好条件的求最优解
抽象性的描述就是:如果将有限的资源分配给多个表达了偏好的人,并尽可能使他们满意(或者根据他们的意愿,尽可能的满足他们的需要)。
这一次主要讲另一个例子,这个例子是学生宿舍分配求最优解问题
但是该代码可以很容易延伸到其他问题- 在线纸牌游戏中的玩家牌桌分配
- 大型编程项目中开发人员的bug分配
- 家庭成员的家务分配
学生宿舍例子
具体描述
import math
import random
import MyOptimization
#一个代表宿舍集合的列表,注意每一个宿舍有两个隔间
dorms=['Zeus','Athena','Hercules','Bacchus','Pluto']
#表述每个学生的第一志愿以及第二志愿
prefs=[('Toby',('Bacchus','Hercules')),
('Steve',('Zeus','Pluto')),
('Andrea',('Athena','Zeus')),
('Sarah',('Zeus','Pluto')),
('Dave',('Athena','Bacchus')),
('Jeff',('Hercules','Pluto')),
('Fred',('Pluto','Athena')),
('Suzie',('Bacchus','Hercules')),
('Laura',('Bacchus','Hercules')),
('Neil',('Hercules','Athena'))]
我们不可能满足所有人的需求。另外,该例子非常小巧,但是在实际生活中,也许人数非常多,而且每间宿舍的隔间可能有4个。
与航班问题相比,最大的困难在于题解了每间宿舍仅限两个学生居住的约束条件。
解决思路
好吧,书上的内容我读懂了,但是我现在未必有很深的领悟。对这个问题的解决方法就是:随意产生一个解,但是这个解必定是有效的,满足条件的。解虽然也是用一个数字列表来表示,但是我们却不能直接看出某个学生选了什么。但是我么保证了这个数字列表在我们的规则之下确实能打印出独一无二的结果。此外,我们每次用这个有效解计算成本,选择成本最小的。核心思路如下:
将所有的宿舍用槽来表示,每个宿舍两个槽。共有10个槽,相同宿舍的槽用同样的数字表示,当某一个槽被选了之后,我们将会将其删除出槽列表。如下所示:
[0,0,1,1,2,2,3,3,4,4]
如果第一个学生选了第一个,槽列表将剩余:
[0,1,1,2,2,3,3,4,4]
依次,槽列表越来越少。
现在,我们需要一个domain,就是范围,有这个范围内产生的一系列数字,并不是代表学生选择了哪一个宿舍,只是代表了学生选择剩余槽内的第几号元素。比如:[0,0,0,0,0,0,0,0,0,0],它可以存在,为什么呢?因为它只是代表了每一位学生都选择了槽内的第一个元素。而是每次剩余槽内的第一个元素并都代表第一个宿舍。
比如[1,1,1,1,1,1,1,1,1,1]确实无效的,为什么?因为轮到最后一个选的时候,槽内只有一个了,他却要选第二个,显然已经数组越界了。
所以产生的这个domain的范围确是:
#[(0,9),(0,8),(0,7),(0,8).....(0,0)]
domain=[(0,(len(dorms)*2)-i-1) for i in range(0,len(dorms)*2)]代码
#最关键的就是传入的vec这个序列的含义了
#比如[0,0,0,0,0,0,0,0,0,0]
#这并不代表某一个学生要选择dorms里面的第一个宿舍
#它代表的含义是选择了剩余槽列表里面的第一个。
def printsolution(vec):
slots=[]
#每个宿舍两个槽
for i in range(len(dorms)):slots+=[i,i]
print slots
#遍历每一个学生的安置情况
for i in range(len(vec)):
x = int(vec[i])
print slots
#从剩余槽中选择
dorm=dorms[slots[x]]
print prefs[i][0],dorm
#删除该槽
del slots[x]
上述函数可以帮助我们打印出最终学生的选择,下面一个成本函数。成本函数的参数和printsolution是一I样的,我们针对每一个有效解(千万注意:该有效解不能直接看出某个选择选择了什么),计算了成本,如果成本低,我们就会保留。
成本函数:
def dormcost(vec):
cost=0
#建立一个槽序列
slots=[]
#每个宿舍两个槽
for i in range(len(dorms)):slots+=[i,i]
#遍历每一个学生
for i in range(len(vec)):
x=int(vec[i])
dorm=dorms[slot[x]]
pref=prefs[i][1]
#首选成本值为0,次选成本值为1
if pref[0]==dorm:cost+=0
elif pref[1]==dorm:cost+=1
else cost+=3#不在选择之列则成本为3
#删除选中的槽
del slots[x]
return cost有了上面两个函数,我们只需要像之前解决航班问题一样,将domain和成本函数传入到求最优解的函数或者是随机搜索就可以了。
经过我实际运行,确实产生了最优解,非常棒。
在文档开头加入:import MyOptimization
代码:
#[(0,9),(0,8),(0,7),(0,8).....(0,0)]
domain=[(0,(len(dorms)*2)-i-1) for i in range(0,len(dorms)*2)]
sol=MyOptimization.geneticoptimize(domain,dormcost)
printsolution(sol)知识迁移能力很重要,希望这道题的解答过程能够深深地印在我的脑海了。
网络可视化
含义
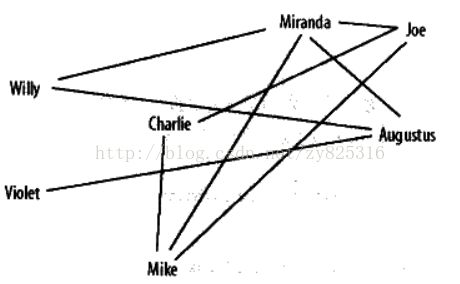
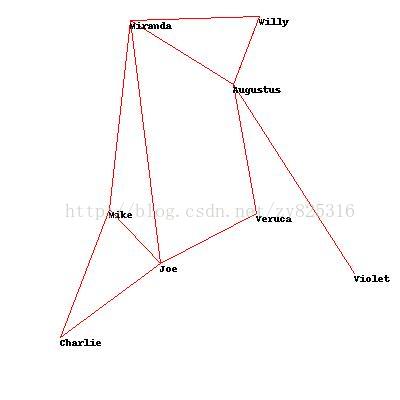
一切高深的问题用例子来讲都可以讲的很简单,这是一个在社交网络的运用,我们想搞清楚人们之间的联系,如果用图可以直接看出来将是非常方便的。如下图所示:
这是一个有点乱的网格,虽然能看出来谁是谁的朋友,但是显然看不出一些关键人物,对比另外一幅图。
ok,这一小节,主要就是将怎么利用数据做出上一幅图。当然其中会使用到求最优解的算法。为什么?因为我们为了看清楚一幅图,我们总希望交叉线最少,我们总希望角度最好大一点...等等,所有在可以产生的那么多图中,我们想找到我们能看的最清楚的那一幅图
准备工作
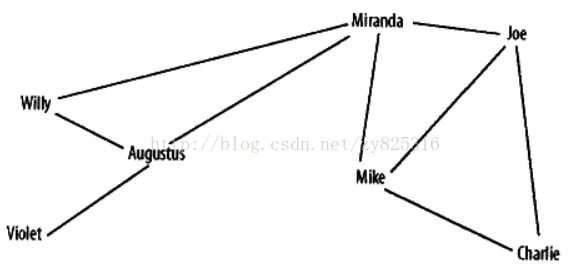
我们需要一点数据,来完成我们这次的学习,如下图所示:
import math
people=['Charlie','Augustus','Veruca','Violet','Mike','Joe','Willy','Miranda']
links=[('Augustus','Willy')
('Mike','Joe')
('Miranda','Mike')
('Violet','Augustus')
('Miranda','Willy')
('Charlie','Mike')
('Veruca','Joe')
('Miranda','Augustus')
('Willy','Augustus')
('Joe','Charlie')
('Veruca','Augustus')
('Miranda','Joe')
]
我们要做的事就是:开发一个程序,能够读出上面的数据,主要是谁是谁的好朋友,然后画出一个视觉上方便的图。
核心思维
画图的核心思维或者算法就是 质点弹簧法(mass-and-spring algorithm).算法受物理学启发:各个节点相互之间都有推力,将彼此分离,但是如果彼此有联系,则拉近一点点。这样的话,没有关联的点就会被推在外面,而彼此连接紧密的节点在拉在了一起。
然而,质点弹簧法无法避免交叉线,交叉线越多,观察越困难。然而,这就是我们需要求最优解函数的地方。我们可以设置一个成本函数。最简单的办法:成本函数就是计算交叉线的个数。
如何计算交叉线的个数呢?有两个关键关键1就是如何表达题解呢?我们用坐标的方式的,每一个人都有一个x坐标和一个y坐标,所以把这些所有的坐标一次放在一个数字列表中就可以,比如:
sol=[120,200,250,125.....
这表示第一个人charlie位置坐标(120,200)的地方。
关键2就是计算交叉点的方式使用了一个公式:分数值。两条线,不平行肯定交叉,但是我们题中出现的线段,所以我们主要考察线段是否交叉。对两个线段分别求出分数值:如果分数值的范围在0到1之间,那么就交叉,不然就不交叉。
成本函数的接受一个题解,然后遍历所有的一对线段,判断是否交叉,每交叉一次,我们就交成本增加1.
代码
接着来让我们看一下求成本的代码(也就是交叉线):def crosscount(v):
#将数字序列转化为一个person:(x,y)的字典
loc=dict([(people[i],(v[i*2],v[i*2+1])) for i in range(0,len(people))])
total=0
#遍历每一对连线
for i in range(len(links)):
for j in range(i+1,len(links)):
#获得坐标位置
(x1,y1),(x2,y2)=loc[links[i][0]],loc[links[i][1]]
(x3,y3),(x4,y4)=loc[links[j][0]],loc[links[j][1]]
#下列几个算式涉及一个数学公式。不要太在意其复杂的表达方式,它只是遵循了数学公式
den=(y4-y3)*(x2-x1)-(x4-x3)*(y2-y1)
#如果两线平行,则den==0
if den==0:continue
#否则,ua与ub就是两条交叉线的分数值
#如果要显示成小数点那样的形式,必须要用float,这个很重要。这是与书上不同的地方
ua=float(((x4-x3)*(y1-y3)-(y4-y3)*(x1-x3)))/float(den)
ub=float(((x2-x1)*(y1-y3)-(y2-y1)*(x1-x3)))/float(den)
#如果两条线的分数值介于0和1之间,则两线彼此交叉
if ua>0 and ua<1 and ub>0 and ub<1:
total+=1
return total
上述与书中不同的主要就是那个float,不加float的话,产生的数是四舍五入之后的数。
接着,我们可以用如下代码产生一个优秀的题解:
注意引入MyOptimization.py
#因为我们决定将我们的坐标系建立在一个400*400的像素图中,下面写10-370是为了留点边缘,
#所以我们可以可以知道每一个坐标的x或者y的范围都是10到370,而每一个人有x和y坐标,所以要乘以2
domain=[(10,370)]*(len(people)*2)
sol=MyOptimization.geneticoptimize(domain,crosscount)
print sol我们现在已经求出最优解了,我们还想把它画出来。
画出来必须使用一个库文件,说白了就画图的呗。库的名字叫做 Python Imaging Library。安装过程很简单,直接去 下载,然后对应自己python版本下载一个,当然也要注意自己的平台。
然后就是代码,其实代码部分非常简单(不过让自己写还真的未必写的出来)
from PIL import Image,ImageDraw
def drawnetwork(sol):
#建立image对象
img=Image.new('RGB',(400,400),(255,255,255))
draw=ImageDraw.Draw(img)
#建立一个字典,准备打印位置,和上面计算成本一个意思
pos=dict([(people[i],(sol[i*2],sol[i*2+1])) for i in range(0,len(people))])
#划线,也就是说不会刻意去画点,全是线。
for (a,b) in links:
draw.line((pos[a],pos[b]),fill=(255,0,0))
#把人物名字绘制出来,看着人名就知道哪里是个点了吧
for n,p in pos.items():
draw.text(p,n,(0,0,0))
img.show()由于每次产生的题解都是不同的,所以每次画出来的图都不一样,但是现在可以看出来确实非常有趣了。下面贴一幅产生的图
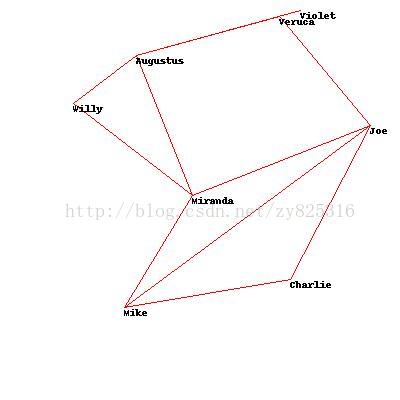
但是这个图很丑(实际上很不错,我产生了很多次才产生出这个图的),关键是
- 两线夹角非常小
- 两点间的间距很近
为了画出好看的图,我们想要杜绝上述两种情况,以一个为例,如果我们不想要两个点靠的太近,那么我们可以里面的每对点进行遍历,如果像素靠的太近了,我们就加一点成本。在本题中,如果两点靠近的50个像素。就多加点成本,具体加了多少请看代码。
代码是在crosscount函数中先添加了一部分(在最后return之前):
def crosscount(v):
#将数字序列转化为一个person:(x,y)的字典
loc=dict([(people[i],(v[i*2],v[i*2+1])) for i in range(0,len(people))])
total=0
#遍历每一对连线
for i in range(len(links)):
for j in range(i+1,len(links)):
#获得坐标位置
(x1,y1),(x2,y2)=loc[links[i][0]],loc[links[i][1]]
(x3,y3),(x4,y4)=loc[links[j][0]],loc[links[j][1]]
#下列几个算式涉及一个数学公式。不要太在意其复杂的表达方式,它只是遵循了数学公式
den=(y4-y3)*(x2-x1)-(x4-x3)*(y2-y1)
#如果两线平行,则den==0
if den==0:continue
#否则,ua与ub就是两条交叉线的分数值
#如果要显示成小数点那样的形式,必须要用float,这个很重要。这是与书上不同的地方
ua=float(((x4-x3)*(y1-y3)-(y4-y3)*(x1-x3)))/float(den)
ub=float(((x2-x1)*(y1-y3)-(y2-y1)*(x1-x3)))/float(den)
#如果两条线的分数值介于0和1之间,则两线彼此交叉
if ua>0 and ua<1 and ub>0 and ub<1:
total+=2
for i in range(len(people)):
for j in range(i+1,len(people)):
#获得两个结点的位置
(x1,y1),(x2,y2)=loc[people[i]],loc[people[j]]
#计算两结点之间的距离
dist=math.sqrt(math.pow(x1-x2,2)+math.pow(y1-y2,2))
#对间距小于50个像素的结点进去判罚。
if dist<150:total+=(1.0-(dist/150.0))
return total
然后我也改了改其中的数据,产生了两幅还不错的图。
总结
算法的应用场合也许有很多,但是看你是否去用心思考。
所有的难点在于:
- 确定题解的表示法
- 成本函数的确定
具体来说,什么样的问题能够使用求最优解的算法来解决呢?书中提出两点
- 问题本身有一个定义好的成本函数
- 相似的解会产生相似的结果
对项目的思考
全部源代码
旅游例子
# -*- coding: cp936 -*-
import time
import random
import math
#将要去旅行的人,第一个是名字,第二个是目前所在地
people = [('Seymour','BOS'),
('Franny','DAL'),
('Zooey','CAK'),
('Walt','MIA'),
('Buddy','ORD'),
('Les','OMA')]
#他们都要到美国的纽约集合,这是旅行的目的地
#LGA是纽约的机场
destination = 'LGA'
#我们将所有的航班信息读到一个字典内,以起止点为键,其他的为值
flights={}
for line in file('schedule.txt'):
origin,dest,depart,arrive,price = line.strip().split(',')
#其中setdefault是作为字典类的一个方法,主要的作用是应对一种情况:当一个键对应多个值,每一个值是一个元组,多个元组组成一个列表,
#说白了,一个键对应一个列表,列表内有许多的元组,一个元组代表一个航班信息
#setdefault的含义是:"如果没有,就设置",如果有,就添加。
flights.setdefault((origin,dest),[])
#现在我们一行一行的把航班信息加入进去
#我认为,我们是对一个列表作为值,所以最外面是一个[]
#里面跟了一个元组,这个元组就是键
flights[(origin,dest)].append((depart,arrive,int(price)))
#通过print flight,我们可以看出在该字典中具体的存储情况。一个起止点作为一个值,对应了一个列表,而列表中有许多元组,每一个元组都是一个航班信息的起飞时间、降落时间和价格
def getminutes(t):
#strptime是将特定的时间格式转化为元组。
x=time.strptime(t,'%H:%M')
return x[3]*60+x[4]
#我觉得x[0]x[1]x[2]是年月
def printschedule(r):
for d in range(len(r)/2):#针对每一个人打印两个航班信息,我们只用重复r的一半次
name=people[d][0]
origin= people[d][1]
out=flights[(origin,destination)][r[2*d]]
ret=flights[(destination,origin)][r[2*d+1]]
print '%10s%10s %5s-%5s $%3s %5s-%5s $%3s' % (name,origin,out[0],out[1],out[2],ret[0],ret[1],ret[2])
def schedulecost(sol):
totalprice=0
latestarrival=0#最晚到底时间
earliestdep=24*60#最早离开时间,现在24*60是最好的情况,等一下会根据实际飞机情况发生改变
for d in range(len(sol)/2):
#得到每一个人的两次航班的价格并且加入到总价格中
origin = people[d][1]
outbound = flights[(origin,destination)][int(sol[2*d])]
returnf = flights[(destination,origin)][int(sol[2*d+1])]
#把钱加入到总价格里面去
totalprice+=outbound[2]
totalprice+=returnf[2]
#根据实际情况改变最晚到达时间和最早离开时间
if latestarrivalgetminutes(returnf[0]):earliestdep=getminutes(returnf[0])
#每一个人必须在机场等待直到最后一个来了才能出发
#每一个人必须在旅游结束时,为了最早离开的人能够赶上飞机,而来到机场等候
totalwait=0
for d in range(len(sol)/2):
origin = people[d][1]
outbound = flights[(origin,destination)][int(sol[2*d])]
returnf = flights[(destination,origin)][int(sol[2*d+1])]
totalwait+=latestarrival-getminutes(outbound[1])
totalwait+=getminutes(returnf[0])-earliestdep
if latestarrivaldomain[j][0]:
#如果很熟悉
neighbors.append(sol[0:j]+[sol[j]-1]+sol[j+1:])
if sol[j]0.5:
#产生一个随机数,决定这次改变是改变数列中的哪一个随机数
i=random.randint(0,len(domain)-1)
#选择一个改变的方向,也就是说是增加还是减少
dir=random.randint(-step,step)
#复制随机解,然后对随机解进行改变,然后判断到底新的解好,还是后来产生的解好
vecb=vec[:]
vecb[i]+=dir
#这一段主要还是不让它超不过了最大最小值的限制
if vecb[i]domain[i][1]:vecb[i]=domain[i][1]
#计算新产生的两次解的成本,然后对成本进行比较
ea=costf(vec)
eb=costf(vecb)
#or后面:表示接受更差的结果。仔细想想,原来概率的表示是如此完成的,注意前一个random()产生的数是在0到1之间。
if(ebdomain[i][0]:
return vec[0:i]+[vec[i]-step]+vec[i+1:]
elif vec[i] 宿舍分配例子
# -*- coding: cp936 -*-
import math
import random
import MyOptimization
#一个代表宿舍集合的列表,注意每一个宿舍有两个隔间
dorms=['Zeus','Athena','Hercules','Bacchus','Pluto']
#表述每个学生的第一志愿以及第二志愿
prefs=[('Toby',('Bacchus','Hercules')),
('Steve',('Zeus','Pluto')),
('Andrea',('Athena','Zeus')),
('Sarah',('Zeus','Pluto')),
('Dave',('Athena','Bacchus')),
('Jeff',('Hercules','Pluto')),
('Fred',('Pluto','Athena')),
('Suzie',('Bacchus','Hercules')),
('Laura',('Bacchus','Hercules')),
('Neil',('Hercules','Athena'))]
#最关键的就是传入的vec这个序列的含义了
#比如[0,0,0,0,0,0,0,0,0,0]
#这并不代表某一个学生要选择dorms里面的第一个宿舍
#它代表的含义是选择了剩余槽列表里面的第一个。
def printsolution(vec):
slots=[]
#每个宿舍两个槽
for i in range(len(dorms)):slots+=[i,i]
#遍历每一个学生的安置情况
for i in range(len(vec)):
x = int(vec[i])
#从剩余槽中选择
dorm=dorms[slots[x]]
print prefs[i][0],dorm
#删除该槽
del slots[x]
def dormcost(vec):
cost=0
#建立一个槽序列
slots=[]
#每个宿舍两个槽
for i in range(len(dorms)):slots+=[i,i]
#遍历每一个学生
for i in range(len(vec)):
x=int(vec[i])
dorm=dorms[slots[x]]
pref=prefs[i][1]
#首选成本值为0,次选成本值为1
if pref[0]==dorm:cost+=0
elif pref[1]==dorm:cost+=1
else: cost+=3#不在选择之列则成本为3
#删除选中的槽
del slots[x]
print cost
return cost
#[(0,9),(0,8),(0,7),(0,8).....(0,0)]
domain=[(0,(len(dorms)*2)-i-1) for i in range(0,len(dorms)*2)]
sol=MyOptimization.geneticoptimize(domain,dormcost)
printsolution(sol)社交网络绘图
# -*- coding: cp936 -*-
import math
import MyOptimization
from PIL import Image,ImageDraw
people=['Charlie','Augustus','Veruca','Violet','Mike','Joe','Willy','Miranda']
links=[('Augustus','Willy'),
('Mike','Joe'),
('Miranda','Mike'),
('Violet','Augustus'),
('Miranda','Willy'),
('Charlie','Mike'),
('Veruca','Joe'),
('Miranda','Augustus'),
('Willy','Augustus'),
('Joe','Charlie'),
('Veruca','Augustus'),
('Miranda','Joe')]
def crosscount(v):
#将数字序列转化为一个person:(x,y)的字典
loc=dict([(people[i],(v[i*2],v[i*2+1])) for i in range(0,len(people))])
total=0
#遍历每一对连线
for i in range(len(links)):
for j in range(i+1,len(links)):
#获得坐标位置
(x1,y1),(x2,y2)=loc[links[i][0]],loc[links[i][1]]
(x3,y3),(x4,y4)=loc[links[j][0]],loc[links[j][1]]
#下列几个算式涉及一个数学公式。不要太在意其复杂的表达方式,它只是遵循了数学公式
den=(y4-y3)*(x2-x1)-(x4-x3)*(y2-y1)
#如果两线平行,则den==0
if den==0:continue
#否则,ua与ub就是两条交叉线的分数值
#如果要显示成小数点那样的形式,必须要用float,这个很重要。这是与书上不同的地方
ua=float(((x4-x3)*(y1-y3)-(y4-y3)*(x1-x3)))/float(den)
ub=float(((x2-x1)*(y1-y3)-(y2-y1)*(x1-x3)))/float(den)
#如果两条线的分数值介于0和1之间,则两线彼此交叉
if ua>0 and ua<1 and ub>0 and ub<1:
total+=2
for i in range(len(people)):
for j in range(i+1,len(people)):
#获得两个结点的位置
(x1,y1),(x2,y2)=loc[people[i]],loc[people[j]]
#计算两结点之间的距离
dist=math.sqrt(math.pow(x1-x2,2)+math.pow(y1-y2,2))
#对间距小于50个像素的结点进去判罚。
if dist<150:total+=(1.0-(dist/150.0))
return total
def drawnetwork(sol):
#建立image对象
img=Image.new('RGB',(400,400),(255,255,255))
draw=ImageDraw.Draw(img)
#建立一个字典,准备打印位置,和上面计算成本一个意思
pos=dict([(people[i],(sol[i*2],sol[i*2+1])) for i in range(0,len(people))])
#划线,也就是说不会刻意去画点,全是线。
for (a,b) in links:
draw.line((pos[a],pos[b]),fill=(255,0,0))
#把人物名字绘制出来,看着人名就知道哪里是个点了吧
for n,p in pos.items():
draw.text(p,n,(0,0,0))
img.show()
img.save('未改进的图.jpg','JPEG')
#因为我们决定将我们的坐标系建立在一个400*400的像素图中,下面写10-370是为了留点边缘,
#所以我们可以可以知道每一个坐标的x或者y的范围都是10到370,而每一个人有x和y坐标,所以要乘以2
domain=[(10,370)]*(len(people)*2)
sol=MyOptimization.geneticoptimize(domain,crosscount)
print drawnetwork(sol)
代码和数据已上传至网盘:
mydorm.py
MyOptimization.py
mysocialnetwork.py
schedule.txt