阿里云超级码力第二场记录
前天参加了这场比赛,当时记错时间了,差点晚了半个小时QAQ。
过程中一直卡在第一题,不过结果挺好的,做出了3个题,239名。
算是混了件T恤(然而信息没有填写完整,不知道还能不能搞得到)
这里就先把前三题的题解放在这里同大家分享。
三角魔法
题目链接
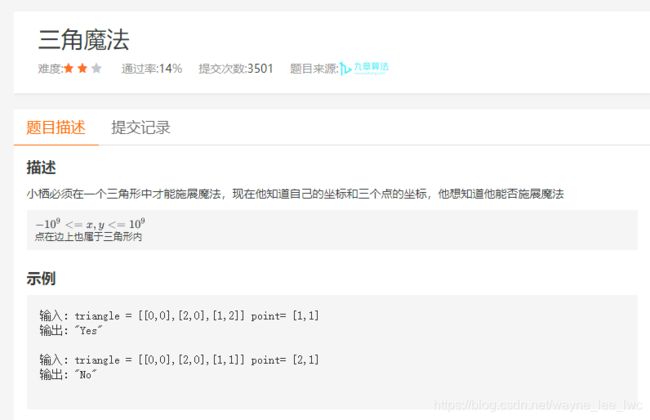
这道题简单来说,就是需要我们判断某个点是否在三角形内。题目给定我们三角形三个顶点的坐标以及一个待判断的点。
解决这个问题我们需要一些数学上的知识:叉积
我们设有向量:
a ⃗ = [ x 1 y 1 z 1 ] b ⃗ = [ x 2 y 2 z 2 ] \vec{a} = \begin{bmatrix} x_1\\y_1\\z_1 \end{bmatrix} \vec{b} = \begin{bmatrix} x_2\\y_2\\z_2 \end{bmatrix} a=⎣⎡x1y1z1⎦⎤b=⎣⎡x2y2z2⎦⎤
则他们的叉积为:
a ⃗ × b ⃗ = ∣ i ⃗ j ⃗ k ⃗ x 1 y 1 z 1 x 2 y 2 z 2 ∣ \vec{a}\times\vec{b} = \begin{vmatrix} \vec{i} &\vec{j} &\vec{k} \\ x_1& y_1 &z_1 \\ x_2& y_2 &z_2 \end{vmatrix} a×b=∣∣∣∣∣∣ix1x2jy1y2kz1z2∣∣∣∣∣∣
我们知道叉积结果是具有几何意义的,参考这一张图:
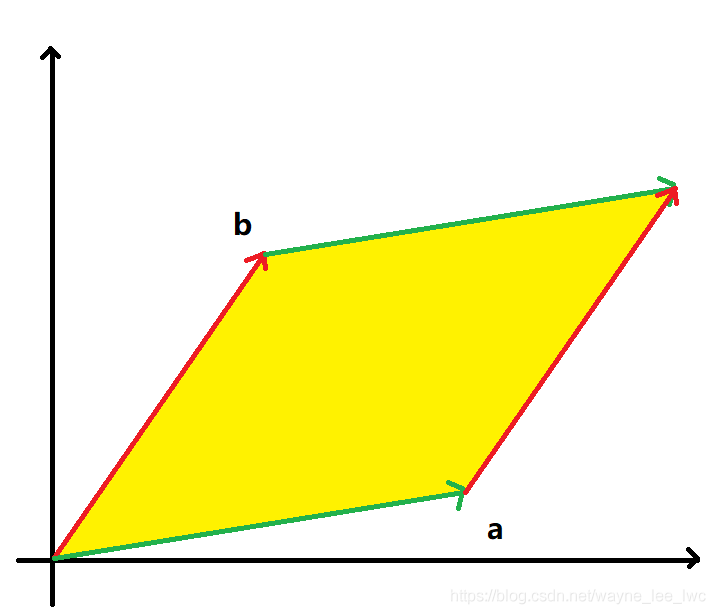
叉积的结果是一个向量,这个向量垂直于向量a和b所在的平面,它的模就是a和b如上图围成的平行四边形的面积。
它的方向同ab满足右手螺旋法则即我们使用右手卷曲四指,四指先穿过a向量再穿过b向量,拇指指向即为结果向量的方向。
特殊的,在二维平面中,所有向量的竖坐标为零,则两个向量的叉积为:
a ⃗ × b ⃗ = ∣ i ⃗ j ⃗ k ⃗ x 1 y 1 0 x 2 y 2 0 ∣ = x 1 y 2 k ⃗ − x 2 y 1 k ⃗ = ( x 1 y 2 − x 2 y 1 ) k ⃗ \vec{a} \times\vec{b}=\begin{vmatrix} \vec{i}&\vec{j}&\vec{k}\\ x_1&y_1&0\\ x_2&y_2&0 \end{vmatrix} =x_1y_2\vec{k} - x_2y_1\vec{k} = (x_1y_2 - x_2y_1)\vec{k} a×b=∣∣∣∣∣∣ix1x2jy1y2k00∣∣∣∣∣∣=x1y2k−x2y1k=(x1y2−x2y1)k
依据这个式子我们根据(x1y2 - x2y1)的符号来判断向量的位置关系。
- 当(x1y2 - x2y1) < 0时a在b的左侧
- 当(x1y2 - x2y1) = 0时ab共线
- 当(x1y2 - x2y1) > 0时a在b的右侧
有了这样的铺垫,这道题我们就可以解决了。
接着,我们从每个顶点向带判断的点构造一个向量:
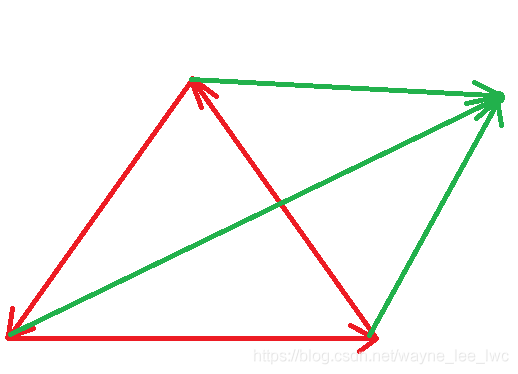
对于每个顶点,我们将以他为始点的两个向量做叉积,根据符号,我们可以判断该点在这条边的那一侧。
可以知道的是,如果该点在所有边向量的同一侧,即所有叉积的值符号相同,那么这个点就在三角形内。如果其中出现叉积为0,那么该点就在某条边上。
由于题目中说到,位于边上的点也算作三角内,
所以我们只需要检测三个叉积中非零的符号即可。
最后,需要注意一种情况(这种情况卡了我n久),就是三点共线且点在该线上。
这个时候三个叉积都是零,排除这个情况,剩下的使用叉积就可以完美解决了。
考虑到,最多可能有连续的两个叉积为0(在顶点处),所以我们可以循环五次,照顾到所有相邻的叉积(主要是第一个和最后一个)
(注意中间不要爆long)
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
import java.util.Scanner;
public class Solution1 {
/*向量类*/
class Vec{
public long x;
public long y;
public Vec(long x,long y) {
this.x = x;
this.y = y;
}
/*向量叉积*/
public long crossProduct(Vec v) {
return x * v.y - y * v.x;
}
}
public String castMagic(List<List<Integer>> triangle, int[] point) {
// write your code here
Vec[] vecTri = new Vec[3];
Vec[] vecSig = new Vec[3];
for(int i = 0;i < 3;i++) {
vecTri[i] = new Vec((long)triangle.get((i + 1) % 3).get(0) - triangle.get(i).get(0),(long)triangle.get((i + 1) % 3).get(1) - triangle.get(i).get(1));
vecSig[i] = new Vec((long)point[0] - triangle.get(i).get(0),(long)point[1] - triangle.get(i).get(1));
}
long flag = 0;
for(int i = 0;i < 5;i++) {
if(flag * vecTri[i % 3].crossProduct(vecSig[i % 3]) < 0) {
return "No";
}else {
flag = sign(vecTri[i % 3].crossProduct(vecSig[i % 3]));
}
}
if(vecTri[0].crossProduct(vecSig[0]) == 0 && vecTri[1].crossProduct(vecSig[1]) == 0 && vecTri[2].crossProduct(vecSig[2]) == 0)
return "No";
return "Yes";
}
/*符号判断*/
private long sign(long a) {
if(a == 0)
return 0;
return a > 0 ? 1 : -1;
}
}
区间异或
题目链接
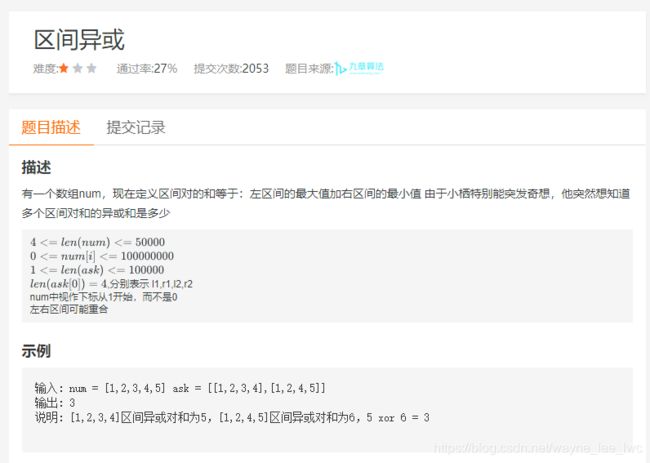
这个题目的主要难点在于快速的求出一个区间内的最大值和最小值。
使用线段树就可以解决这个问题啦。
纪念一下最后12分钟码完一棵线段树一A的神奇事件。最后一分钟一次提交通过是真的很爽!!
import java.util.List;
public class Solution2 {
class Node{
public int l;
public int r;
public int max;
public int min;
public Node left;
public Node right;
}
public int Intervalxor(int[] num, List<List<Integer>> ask) {
Node root = new Node();
create(num,1,num.length,root);
int ans = 0;
for(List<Integer> list : ask) {
ans ^= getMax(root,list.get(0),list.get(1)) + getMin(root,list.get(2),list.get(3));
}
return ans;
}
private void create(int[] num, int l, int r,Node k) {
// TODO Auto-generated method stub
k.l = l;
k.r = r;
if(l == r) {
k.max = num[l - 1];
k.min = num[l - 1];
return;
}
k.left = new Node();
k.right = new Node();
int mid = (l + r) >> 1;
create(num,l,mid,k.left);
create(num,mid + 1,r,k.right);
k.max = Math.max(k.left.max, k.right.max);
k.min = Math.min(k.left.min, k.right.min);
}
private int getMax(Node k,int l,int r) {
if(k.l == l && k.r == r) {
return k.max;
}
int mid = (k.l + k.r) >> 1;
if(r <= mid)
return getMax(k.left,l,r);
else if(l > mid)
return getMax(k.right,l,r);
else
return Math.max(getMax(k.left,l,mid), getMax(k.right,mid + 1,r));
}
private int getMin(Node k,int l,int r) {
if(k.l == l && k.r == r) {
return k.min;
}
int mid = (k.l + k.r) >> 1;
if(r <= mid)
return getMin(k.left,l,r);
else if(l > mid)
return getMin(k.right,l,r);
else
return Math.min(getMin(k.left,l,mid), getMin(k.right,mid + 1,r));
}
}
五字回文
题目链接
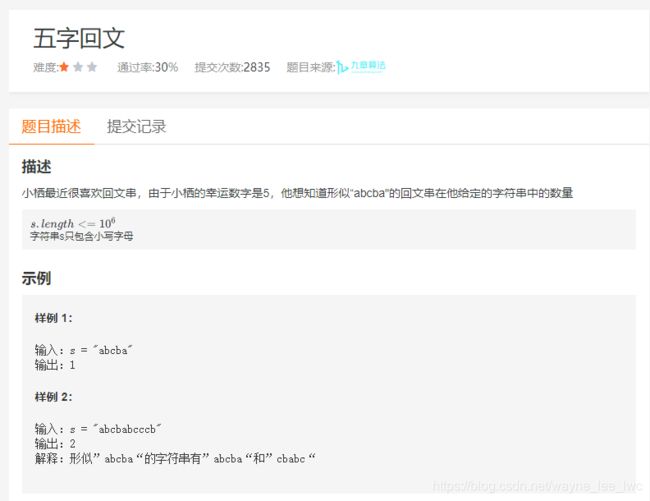
这道题的难度不高,暴力枚举并验证即可。复杂度就是O(m)
需要注意的就是回文串需要时abcba型,即其中的前三个字符不能够相同。
import java.util.Scanner;
public class Solution3 {
public int Fivecharacterpalindrome(String s) {
int ans = 0;
for(int i = 0;i <= s.length() - 5;i++) {
ans += check(s.substring(i, i + 5)) ? 1 : 0;
}
return ans;
}
private boolean check(String substring) {
for(int i = 0;i < 2;i++) {
if(substring.charAt(i) != substring.charAt(5 - i - 1)) {
return false;
}
}
return substring.charAt(0) != substring.charAt(1) && substring.charAt(0) != substring.charAt(2) && substring.charAt(1) != substring.charAt(2);
}
}