数据分析中的统计检验方法- t检验、f检验、卡方检验、互信息

数据的种类

我们都知道，一般数据可以分为两类，即定量数据（数值型数据）和定性数据（非数值型数据），定性数据很好理解，例如人的性别，姓名这些都是定性数据。定量数据可以分为以下几种：

• 定类数据
  表现为类别，但不区分顺序，是由定类尺度计量形成的。一般可以从非数值型数据中编码转换而来，数值本身没有意义，只是为了区分类别做出的数值型标识，比如1表示男性，0表示女性。定类数据无法比较大小，运算符也无意义。

• 定序数据
  表现为类别，但有顺序，是由定序尺度计量形成的。运算符也没有意义，例如比赛中的排名，不能说第一名到第二名之前的差距与第二名到第三名之间的差距相等。

• 定距数据
  表现为数值，可进行加、减运算，是由定距尺度计量形成的。定距数据的特征是没有绝对的零点，例如温度，不能说10摄氏度的一倍是20摄氏度。因此乘、除法对于定距数据来说也是没有意义的。

• 定比数据
  表现为数值，可进行加、减、乘、除运算，是由定比尺度计量形成的。定比数据存在绝对的零点。例如价格，100元的一倍就是200元。

T检验

T检验（T-test）主要是为了比较数据样本之间是否具有显著性的差异。或者是否能从样本推论到整体，例如有某个班的学习成绩的数据，想推论该班上男女生的学习成绩差异大，或者根据数据推论出，整个学校的男女生学习成绩差异都大，需要用到卡方检验。一般用于定量数据的检测（定类数据采用卡方检验），T检验的前提条件是假设样本服从或者近似服从正态分布，T检验是一种参数检验方法（假定总体的分布已知）。
针对不同的场景，主要有以下三种检验方法：

• 独立样本的T检验
  主要用于定量数据和定类数据的差异关系研究，例如有一个班的学生数据，如果学生的成绩服从正太分布，想要研究升高和成绩的关系，就需要用到该方法，如果不服从正态分布，可采用MannWhitney检验。
• 单一样本的T检验
  主要用于检验某单一的定量数据差异，例如一个班的成绩是否显著大于70分。同样需要满足正态分布的假设，若不满足可采用单样本Wilcoxon检验。
• 配对T检验
  检验样本中配对数据的差异性，例如一个班上男、女生的成是否显著差异，不满足正态分布的话，可采用Wilcoxon检验。

T检验主要通过样本均值的差异进行检验，统计学上以“总体间没差别”计算显著性水平H0，拒绝原假设H0的最小显著性水平称为检验的p值.，来检验假设的结果。例如，假设一个班上男女生的成绩不存在差异，显著性水平为0.05，可理解为只有5%的概率会出现“男女生差异显著”的情况，计算出的检验p值若小于0.05，则可以通过原假设。反之拒绝原假设。

此外，两个独立样本的T检验，通常需要先进行F检验（方差齐次检验），检验两个独立样本的方差是否相同，若两总体方差相等，则直接用t检验，若不等，可采用t’检验或变量变换或秩和检验等方法。也就是说进行两独立样本的T检验时，需首先验证两样本的方差是否相同。

python的机器学习工具包scipy中，有统计分析模块stats，其中就有T检验函数：

from scipy import stats
#单一样本的t检验，检验单一样本是否与给定的均值popmean差异显著的函数，第一个参数为给定的样本，第二个函数为给定的均值popmean，可以以列表的形式传输多个单一样本和均值。
stats.ttest_1samp(a, popmean, axis=0, nan_policy='propagate')
#独立样本的T检验，检验两个样本的均值差异，该检验方法假定了样本的通过了F检验，即两个独立样本的方差相同
stats.ttest_ind(a, b, axis=0, equal_var=True, nan_policy='propagate')
#检验两个样本的均值差异（同上），输出的参数两个样本的统计量，包括均值，标准差，和样本大小
stats.ttest_ind_from_stats(mean1, std1, nobs1, mean2, std2, nobs2, equal_var=True)
#配对T检验，检测两个样本的均值差异，输入的参数是样本的向量
stats.ttest_rel(a, b, axis=0, nan_policy='propagate')

F检验

F检验（F-test），最常用的别名叫做联合假设检验（英语：joint hypotheses test），此外也称方差比率检验、方差齐性检验。它是一种在零假设（null hypothesis, H0）之下，统计值服从F-分布的检验。其通常是用来分析用了超过一个参数的统计模型，以判断该模型中的全部或一部分参数是否适合用来估计母体。
其计算过程如下：


计算得到的F值，再与对应F分布表查询，若大于表中的值，则接受原假设（两样本的方差相同），否则拒绝原假设。

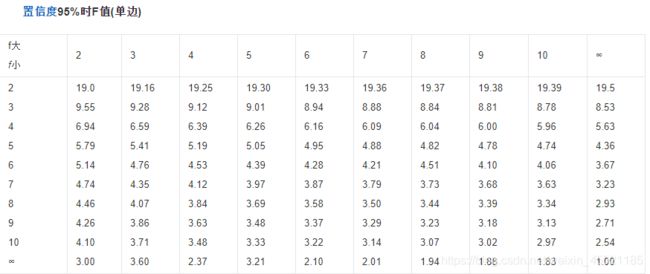
stats模块中虽然没有f检验的函数，但是却有着f分布的生成函数，可以利用其进行f检验：

from scipy.stats import f
F = np.var(a) / np.var(b)
df1 = len(a) - 1
df2 = len(b) - 1
p_value = 1 - 2 * abs(0.5 - f.cdf(F, df1, df2))

也可以引入sklearn进行f检验

from sklearn.feature_selection import f_classif
f_class, pvalue = f_classif(X,y)
print([i for i,p in enumerate(pvalue) if p<0.05 ])#p值

卡方检验

卡方检验（chi-square test），也就是χ2检验，用来验证两个总体间某个比率之间是否存在显著性差异。卡方检验属于非参数假设检验，适用于布尔型或二项分布数据，基于两个概率间的比较，早期用于生产企业的产品合格率等。卡方检验是以χ2分布为基础的一种常用假设检验方法，它的无效假设H0是：观察频数与期望频数没有差别。该检验的基本思想是：首先假设H0成立，基于此前提计算出χ2值，它表示观察值与理论值之间的偏离程度。根据χ2分布及自由度可以确定在H0假设成立的情况下获得当前统计量及更极端情况的概率P。如果当前统计量大于P值，说明观察值与理论值偏离程度太大，应当拒绝无效假设，表示比较资料之间有显著差异；否则就不能拒绝无效假设，尚不能认为样本所代表的实际情况和理论假设有差别。（摘自智库百科）。
　卡方检验的基本公式为：

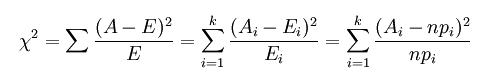
A 为观察值，E为理论值，k为观察值的个数，最后一个式子实际上就是具体计算的方法了 n 为总的频数，p为理论频率，那么n*p自然就是理论频数（理论值）。
卡方检验是以χ2分布为基础的一种常用假设检验方法，χ2分布，就叫做卡方分布。若k 个随机变量Z1、……、Zk 相互独立，且数学期望为0、方差为 1(即服从标准正态分布)，则随机变量X：

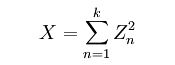
记作：

在做卡方检验时，通常针对的数据主要为定类数据，例如样本中是男生的人数，研究的问题通常是两个类别之间是否有显著关联。
python中stats模块，同样有卡方检验的计算函数，sklearn中的特征选择中也可以进行卡方检验。

from scipy import stats
stats.chi2_contingency(observed, correction=True, lambda_=None)
from sklearn.feature_selection import chi2
chi2_value, pvalue = chi2(X,y)
print([i for i,p in enumerate(pvalue) if p<0.05 ])

互信息

互信息(Mutual Information)是信息论里一种有用的信息度量，它可以看成是一个随机变量中包含的关于另一个随机变量的信息量，1表示完全关联，0表示没有联系。也就是说，互信息可以看成，从某一个随机变量可以获取另外一个随机变量的信息程度。反应在概率上，设x,y为两个随机变量，则有：

我们都知道，熵也是信息增益中的一种概念，按照熵的定义有

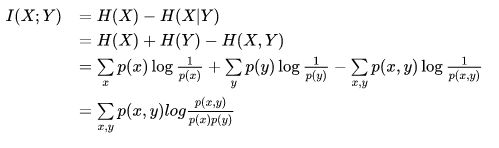
即，加上了Y变量后，对X的变量的熵增加了多少。或理解为x的后验概率和先验概率的比值（的对数），称为互信息。
sklearn中计算互信息较简单

from scipy import stats
stats.chi2_contingency(observed, correction=True, lambda_=None)



from sklearn.feature_selection import mutual_info_classif
minfo = mutual_info_classif(X, y, discrete_features=False ,n_neighbors=3)
print(minfo)

mutual_info_classif中含有两个重要的参数：

• discrete_features：为{‘auto’, bool, array_like}, default ‘auto’，表示特征是否离散，array_like可以指定哪些特征是离散的哪些是连续的
• n_neighbors：int, default 3，n_neighbors是用来估计随机变量互信息的近邻数，大的n_neighbors可以降低估计器的方差，但会造成偏差