Javascript实现BFS算法
在实现BFS算法之前,先建立邻接矩阵和邻接表:
邻接矩阵
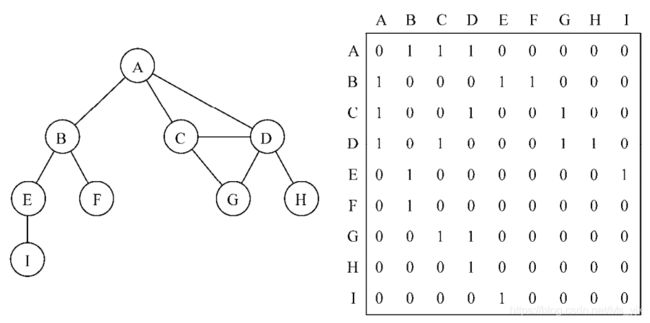
每个节点都和一个整数相关联,该整数将作为数组的索引。用一个二维数组来表示顶点之间的连接。比如上面图片中的图的邻接矩阵表示:
由于该图不是强连通图(如果图中每两个顶点间在双向上都存在路径,则该图是强连通的。例如, C和D是强连通的,而A和B不是强连通的。),所以在矩阵中会出现‘0’值,表示该两节点之间没有连接。、
但是,图中顶点的数量可能会改变,而2维数组不太灵活。一般会选择使用邻接表。
邻接表
动态数据结构,邻接表由图中每个顶点的相邻顶点列表所组成。
两者的不同
1、在邻接矩阵表示中,无向图的邻接矩阵是对称的。矩阵中第 i 行或 第 i 列有效元素个数之和就是顶点的读。
在有向图中 第 i 行有效元素个数之和是顶点的出度,第 i 列有效元素个数之和是顶点的入度。
2、在邻接表的表示中,无向图的同一条边在邻接表中存储的两次。如果想要知道顶点的读,只需要求出所对应链表的结点个数即可。
有向图中每条边在邻接表中只出现一此,求顶点的出度只需要遍历所对应链表即可。求出度则需要遍历其他顶点的链表。
3、邻接矩阵与邻接表优缺点:
邻接矩阵的优点是可以快速判断两个顶点之间是否存在边,可以快速添加边或者删除边。而其缺点是如果顶点之间的边比较少,会比较浪费空间。因为是一个 n∗nn∗n 的矩阵。
而邻接表的优点是节省空间,只存储实际存在的边。其缺点是关注顶点的度时,就可能需要遍历一个链表。还有一个缺点是,对于无向图,如果需要删除一条边,就需要在两个链表上查找并删除。
demo函数创建
创建空图
使用字典进行储存数据,字典中的键值对可以更好地存储节点的信息。字典源码:Javascript实现Dictionary
添加边和顶点的信息
使用push()方法进行添加,图中的有向图和无向图创建的区别就是无向图两个节点之间是互相连通的,对于有向图是单向的。
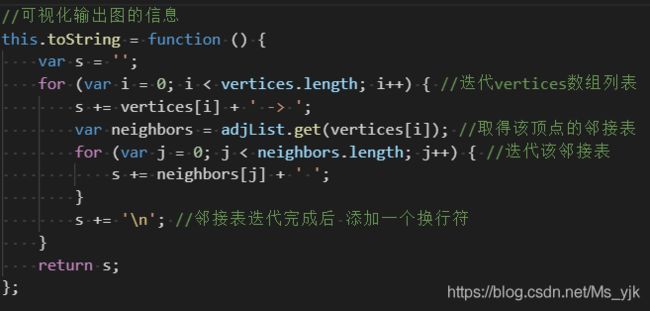
输出函数toString
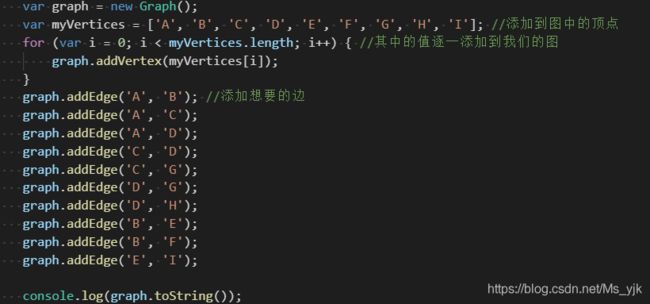
测试邻接表
BFS算法
在BFS算法中,使用队列进行节点信息的存储:通过将顶点存入队列中(在第4章中学习过),最先入队列的顶点先被探索。
BFS搜索路径:
- 创建 BFS 步骤
- (1) 创建一个队列Q。
- (2) 将v标注为被发现的(灰色),并将v入队列Q。
- (3) 如果Q非空,则运行以下步骤:
- (a) 将u从Q中出队列;
- (b) 将标注u为被发现的(灰色);
- (c) 将u所有未被访问过的邻点(白色)入队列;
- (d) 将u标注为已被探索的(黑色)。
访问数组
创建一个数组,保存节点的颜色信息。即表示是否被访问:
var initializeColor = function () {
//创建一个数组 保存相对应节点颜色信息
var color = [];
for (var i = 0; i < vertices.length; i++) {
color[vertices[i]] = 'white'; //赋值 white 表示没有被访问过
}
return color;
};BFS核心demo
创建BFS算法,使用队列。队列源码:Javascript实现Queue
this.bfs = function (v, callback) {
var color = initializeColor(), //初始化所有节点的颜色信息是白色
queue = new Queue(); //存储待访问和待探索的顶点
queue.enqueue(v); //起始定点 直接入队
while (!queue.isEmpty()) { //队列非空
var u = queue.dequeue(), //操作队列,从中移除一个顶点
neighbors = adjList.get(u); //取得包含所有邻点的邻接表
color[u] = 'grey'; // 表示已经访问但未探索
for (var i = 0; i < neighbors.length; i++) { // 对u的每个邻点
var w = neighbors[i]; // 取值
if (color[w] === 'white') { // 如果没有进行访问
color[w] = 'grey'; // 标记访问
queue.enqueue(w); // 将该顶点加入队列中
}
}
color[u] = 'black'; // 已经访问并已经探索完成
if (callback) { // 回调函数...
callback(u);
}
}
};实现及解释过程在以上源码中。
测试之前的图,并输出BFS节点访问顺序:
BFS算法实现最短路径
给定一个图G和源顶点v,找出对每个顶点u, u和v之间最短路径的距离。对于给定顶点v,广度优先算法会访问所有与其距离为1的顶点,接着是距离为2的顶点,以此类推。
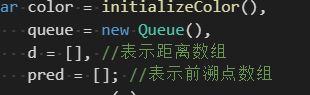
创建两个数组:
- 从v到u的距离d[u];
- 前溯点pred[u],用来推导出从v到其他每个顶点u的最短路径。
改进之后的算法
for (var i = 0; i < vertices.length; i++) { //循环遍历数组赋值
d[vertices[i]] = 0; //用0来初始化数组d 表示距离
pred[vertices[i]] = null; //null来初始化数组pred 存储前溯点
}
while (!queue.isEmpty()) { //队列非空
var u = queue.dequeue(), //操作队列,从中移除一个顶点
neighbors = adjList.get(u); //取得包含所有邻点的邻接表
color[u] = 'grey'; // 表示已经访问但未探索
for (var i = 0; i < neighbors.length; i++) { // 对u的每个邻点
var w = neighbors[i]; // 取值
if (color[w] === 'white') {
color[w] = 'grey';
d[w] = d[u] + 1; //给d[u]加1来设置v和w之间的距离
pred[w] = u; //顶点u的邻点w时,则设置w的前溯点值为u
queue.enqueue(w);
}
}
color[u] = 'black';
}我声明数组d来表示距离,以及pred数组来表示前溯点。下一步则是对图中的每一个顶点,用0来初始化数组d,用null来初始化数组pred。当发现顶点u的邻点w时,则设置w的前溯点值为u。还通过给d[u]加1来设置v和w之间的距离(u是w的前溯点, d[u]的值已经有了)。方法最后返回了一个包含d和pred的对象。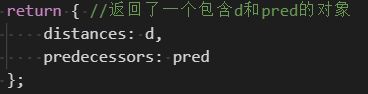
测试改进后的BFS算法
var graph = new Graph();
var myVertices = ['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I']; //添加到图中的顶点
for (var i = 0; i < myVertices.length; i++) { //其中的值逐一添加到我们的图
graph.addVertex(myVertices[i]);
}
graph.addEdge('A', 'B'); //添加想要的边
graph.addEdge('A', 'C');
graph.addEdge('A', 'D');
graph.addEdge('C', 'D');
graph.addEdge('C', 'G');
graph.addEdge('D', 'G');
graph.addEdge('D', 'H');
graph.addEdge('B', 'E');
graph.addEdge('B', 'F');
graph.addEdge('E', 'I');
function printNode(value) {
console.log('Visited vertex: ' + value); //输出值
}
graph.bfs(myVertices[0], printNode); //调用函数
var shortestPathA = graph.BFS(myVertices[0]);
console.log(shortestPathA);输出如下(根据BFS的搜索特点,存储相应的节点距离和前溯点的信息):
输出最短路径
var finalVertexPath = myVertices[0]; //顶点A作为源顶点
for (var i = 1; i < myVertices.length; i++) { //从1开始,去除A节点即源节点
var toVertex = myVertices[i], //顶点数组得到toVertex
path = new Stack(); //创建一个栈存储路径值
for (var v = toVertex; v !== finalVertexPath; v = shortestPathA.predecessors[v]) { //追溯toVertex到finalVertexPath的路径
path.push(v); //变量v添加到栈中
}
path.push(finalVertexPath); //最后添加源顶点
var s = path.pop(); //弹出源定点
while (!path.isEmpty()) {
s += ' - ' + path.pop(); //栈中移出一个项并将其拼接到字符串s的后面
}
console.log(s); //输出路径
}最终的最短路径输出:
BFS源代码:JavaScript实现BFS
时间复杂度
BFS是一种借用队列来存储的过程,分层查找,优先考虑距离出发点近的点。无论是在邻接表还是邻接矩阵中存储,都需要借助一个辅助队列,n个顶点均需入队,最坏的情况下,空间复杂度为O(n)。
邻接表形式存储时,每个顶点均需搜索一次,时间复杂度T1=O(n),从一个顶点开始搜索时,开始搜索,访问未被访问过的节点。最坏的情况下,每个顶点至少访问一次,每条边至少访问1次,这是因为在搜索的过程中,若某结点向下搜索时,其子结点都访问过了,这时候就会回退,故时间复 杂度为O(E),算法总的时间复 度为O(|N|+|E|)。
邻接矩阵存储方式时,查找每个顶点的邻接点所需时间为O(N),即该节点所在的该行该列。又有N个顶点,故算总的时间复杂度为O(|N|^2)。