KMP算法

学习算法的过程是一个需要仔细总结，慢慢积累的过程。很多经典算法看懂了，但不一定能很好的表达出来，因此有必要从自己的角度总结一下学习KMP算法的过程。

KMP算法全称，Knuth-Morris-Pratt算法，是三位算法大牛1977年发表的一个字符串匹配的经典算法。其思想广泛用于字符串匹配相关算法中。

写这篇文章的的时候，其实我并没有看过kmp的完整的算法或者代码，但是看到其它博文中说这个算法采用的避免回溯思想中的冗余计算，并且有几张图简单的示例了算法思想。于是楼主抱着研究的心态，尝试自己根据这个思想来慢慢总结推到出kmp算法。

暴力解法，回溯的思想

在字符串匹配中，最直接的目的导向的算法就是从需要匹配的字符串的第一个字母开始，在源字符串中依次匹配字符。如果遇到一个字符与匹配字符串不一致，那么就从源字符串中下一个字符开始匹配。这就是暴力搜寻方法，用到的是回溯的思想。例如在字符串“abcabe” 中匹配“abe” 字符串，那么

第一次匹配 abc 与 abe，第一个字符不相同，后移一位

第二次匹配 bca 与 abe，第一个字符不相同，后移一位

第三次匹配 cab 与 abe，第一个字符不相同，后移一位

...

这个时间复杂度是 O(n*m) 的，稍微观察可以发现，第二次匹配其实是多余的，原因是根据匹配字符串 “cdf” 的特点，如果前两个字符一致，只是第三个字符不同，那么我们不需要上面的第二次匹配过程。也就是我们不需要回溯到第二个字符。

KMP解法猜想

KMP算法解决了不必要的回溯，减少冗余的计算，加快计算速度。这样就很简单，例如在 “so must i love you so much”中匹配 "so much",

刚开始我们匹配到 "so mus" 与字符串一致，但最后一个字符不一致，我们不需要回溯到第二的字符重新开始匹配，只需要从不一致的字符 “t“ 这里重新开始匹配即可。

但是，还有一些奇怪的情形，我们不能直接从不匹配的那个字符开始匹配。例如匹配如下字符串

”aaat“

”bbsbbt“

这些匹配的字符串有一个共同点，就是他们内部的元素是有重复的。于是我们需要考虑匹配字符串的具体特点来决定下一步回溯到什么位置，来重新开始匹配。这样是否可以在匹配之前，依次分析匹配字符串的每个字符，分析是否需要回溯到第一个元素进行匹配。 特殊的，当元素中没有重复元素的时候，如果匹配到第i个元素，然后发现字符串不匹配，这时候不需要回溯到匹配起点重新开始，只需要从当前位置开始重新匹配。

具体实现，建议一个大小等于匹配字符串长度的数据，标记每个位置是否需要回溯到起点位置重新匹配。

KMP解法

有了自己的理解，再回头看看KMP算法是如何做到的。果然最好的算法比自己考虑的情况更多更全。但是欣慰的是，真正的KMP算法也是采用额外的数据标记的方法来确认回溯大小的。跟我的猜想不一样的，更先进的是，kmp算法中不是标记是否需要回溯到第一个元素重新匹配，而是标记了需要回溯到第几个元素进行匹配。比我的猜想提高不少！！原因是我考虑的情况还是太简单。

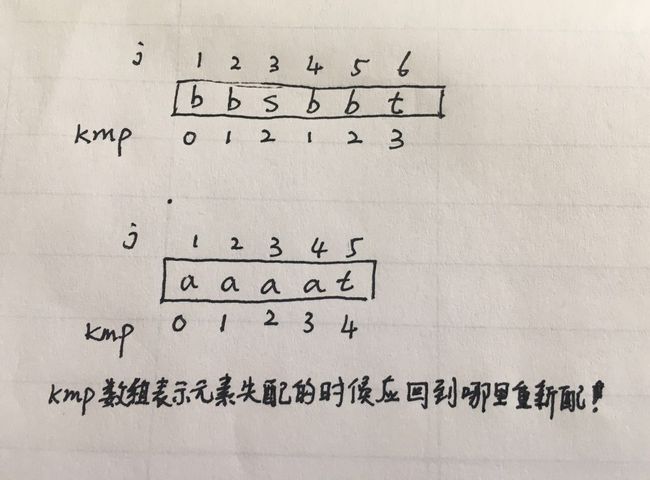
下面两个实际例子。当匹配的字符串是”bbsbbt“，”aaaat“ 的时候如何创建kmp数组。

匹配的字符串的时候分两步，

首先根据字符串做一次循环操作，根据每个位置前面字符特点，即前半段和后半段重复字符的特殊，创建kmp数组。

然后对待搜寻的字符串进行一次循环，进行匹配字符操作，当某个字符不匹配时，根据字符位置处kmp数组的数值返回到不同位置进行重新字符串匹配检查。

算法思想很简单，但是实现没有bug的程序还有有难度，这里贴上java版本的next数组创建，和匹配字符串的程序。来自这个博客

public class KMP {  
  
    void getNext(String pattern, int next[]) {  
        int j = 0;  
        int k = -1;  
        int len = pattern.length();  
        next[0] = -1;  
  
        while (j < len - 1) {  
            if (k == -1 || pattern.charAt(k) == pattern.charAt(j)) {  
  
                j++;  
                k++;  
                next[j] = k;  
            } else {  
  
                // 比较到第K个字符，说明p[0——k-1]字符串和p[j-k——j-1]字符串相等，而next[k]表示  
                // p[0——k-1]的前缀和后缀的最长共有长度，所接下来可以直接比较p[next[k]]和p[j]  
                k = next[k];  
            }  
        }  
  
    }  
  
    int kmp(String s, String pattern) {  
        int i = 0;  
        int j = 0;  
        int slen = s.length();  
        int plen = pattern.length();  
  
        int[] next = new int[plen];  
  
        getNext(pattern, next);  
  
        while (i < slen && j < plen) {  
  
            if (s.charAt(i) == pattern.charAt(j)) {  
                i++;  
                j++;  
            } else {  
                if (next[j] == -1) {  
                    i++;  
                    j = 0;  
                } else {  
                    j = next[j];  
                }  
  
            }  
  
            if (j == plen) {  
                return i - j;  
            }  
        }  
        return -1;  
    }  
  
    /** 
     * @param args 
     */  
    public static void main(String[] args) {  
        // TODO Auto-generated method stub  
        KMP kmp = new KMP();  
        String str = "abababdafdasabcfdfeaba";  
        String pattern = "abc";  
        System.out.println(kmp.kmp(str, pattern));  
    }  
  
} 

思考：

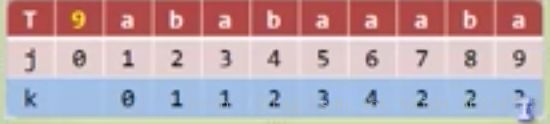
如果匹配字符串是 ”ababaaaaba“， 那么kmp数组应该是多少? 答案在博客最后。

实战练习

leecode上的一道字符串匹配题目，https://leetcode.com/problems/repeated-substring-pattern/

检查字符串时候由重复的字符串叠加而成，例如输入如下字符串，程序应该返回 True。

”abab“

"abcabcabcabc"

好了，上面就是我学习算法的总结。果然自己想出来的比直接看结果理解效果更好。同时可以看到，对于具体问题，经典的解法其实比我们想到的要全面的多。在学习了基础之后，学人所长避免自己走一些探索的弯路。看明白了之后也许会说 ”原来也就如此嘛“。实际上经典kmp算法也还有改进空间的。

参考：

博客参考了 youtude视频 的思路。多学习思想，总结思考问题的方法，而不是追求答案。