机器学习中的常用分布
基本概念：
1. 样本空间
：实验所有可能的输出
的集合。
2. 随机变量
：随机变量是一个映射（或函数），将映射到实数集。可以分为离散型随机变量和连续型随机变量。
3. pmf和pdf：pmf（probability mass function）为离散型随机变量
的概率分布，定义为
，有是也写成f(x)；对于连续型随机变量，则p称为pdf（probability density function），其定义为：
；统称为概率密度函数。
4. cdf：cdf（cumulative distribution function）累计分布函数可以看做是概率密度函数的积分，其定义为：
，取值范围是[0, 1]。
一般情况下提到的分布是指pdf，即概率密度函数（离散或连续）。
以下公式中的p都是概率的含义！
伯努利分布：
最简单的分布，假设随机变量为投一枚硬币的结果，则满足参数为
的伯努利分布，记为：
；
伯努利分布的pdf为：
，x为1或0。
二项分布：
随机变量为进行n次伯努利实验的结果，比如投n次硬币，正面朝上的次数，满足参数为n和的二项分布，记为：
；
二项分布的的pdf为：
，其中
是二项式第x项的系数，故称为二项分布。
多元贝努利分布：
之前一直把二项分布和多元贝努利分布搞混！不知道以下理解是否正确。
二项分布是某个特定的贝努利实验进行了N次，而多元贝努利分布是做了N个不同的贝努利实验！
所以N元贝努利分布应该写成：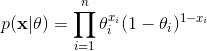
，注意这里的x和theta都是向量，xi表示第i个贝努利实验的结果（1或0），thetai表示第i个贝努利实验的参数（xi=1的概率）。
多项分布：
多项分布是二项分布的一个推广，假设有一个K面的骰子，投掷n次的结果为随机变量，其中的每一个值为一个向量
，其中xj表示抛到第j面的次数，此时满足多项分布，记为：
，其中是一个向量
，每一维表示得到第j面的概率。
多项分布的pdf为：
，其中
。
当K=2时，多项分布退化为二项分布；当n=1时，多项分布退化为Categorical分布。
Categorical分布：
当n=1时的二项分布，伯努利分布的一种推广，即随机变量为投一次骰子的结果，满足Categorical分布，记为：
，其中是与多项分布中相同的一个向量。
Categorical分布的pdf为：
。
gamma函数：
gamma函数是阶乘（n!）在实数域和复数域上的推广，即做一条连续的曲线依次通过n!的所有点（1,2,6,24...），该曲线即为gamma函数。
gamma函数的定义为：
，完全不知道这是什么鬼！是欧拉想出来的，只要记住gamma函数是阶乘在实数域上的推广，当然gamma就有阶乘的性质，
（x为实数），
（n为正整数）。
gamma分布：
对于随机变量（大于0），gamma分布为
。
gamma分布的pdf：
。
现在完全不知道gamma分布是干嘛用的，之后了解了再来这里进行补充！
Beta分布：
Beta分布是二项分布的共轭先验分布，假设随机变量满足Beta分布，则记为：
。
Beta分布的pdf为：
。
既然说Beta分布是二项分布的共轭先验，那么两者之间一定有很强的关联。对比Beta分布的pdf和二项分布的pdf，再根据gamma函数就是阶乘的推广，其实他们俩的形式几乎是一模一样的！只是二项分布和Beta分布的参数与变量的位置好像是相反的！二项分布的参数作为底数，而Beta分布的变量作为底数。好吧，这里要好好理解一下共轭先验是什么鬼了！
共轭先验：
首先要说明的是贝叶斯学派和频率学派一个重要的区别就是，频率学派认为模型的参数是客观存在且不变的，虽然不知道，但可以通过大量的样本估计得到；而贝叶斯学派认为模型的参数也是一个随机变量，满足一定的分布，这也是共轭先验产生的源头。
假设现在的问题是已知样本，要根据样本推测模型参数，即求
。
根据贝叶斯公式可以得到：
，其中是后验概率密度函数，
是似然函数，
是先验概率密度函数。上面的贝叶斯公式说明当我们有新的观测数据x时，我们可以通过新的观测数据修改模型参数。
那么什么是共轭先验分布呢，先上定义：在贝叶斯概率理论中，如果后验概率和先验概率满足同样的分布律，那么，先验分布和后验分布被叫做共轭分布，同时，先验分布叫做似然函数的共轭先验分布。
假设上面的样本来自二项分布，先验分布为Beta分布，带入上式中会发现后验分布也是一个Beta分布。也就是说Beta分布是二项分布的共轭先验分布。
对于某个分布，当我们对参数没有任何先验知识时，可以认为参数满足一个均匀分布（熵最大，风险最小原则）。或者我们可以把似然函数的共轭先验分布作为参数的分布。这样做有两点好处，第一由于先验是似然的共轭先验分布，所以后验和先验是共轭分布，符合直观的理解；第二对于得到的后验分布，可以作为下一轮的先验分布，形成对参数的估计链。贝叶斯学派的思想就是为模型参数构建一个分布，然后用超参数（先验分布的参数）来控制模型的参数！
Dirichlet分布
Dirichlet分布是多项分布的共轭先验分布，是Beta分布在高维上的推广！
Dirichlet分布的pdf为：
，其中
。
与Beta分布和二项分布的关系一样，Dirichlet分布是多项分布的共轭先验，他们在形式上也非常接近，多项分布中的参数是底数，而Dirichlet分布的变量是底数。
是超参数，用来控制二项分布的参数。