【洛谷P5652】基础博弈练习题——杨子曰题目

【洛谷P5652】基础博弈练习题——杨子曰题目

题目背景
YSGH is our red sun.

题目描述
YSGH和YGSH在打膈膜，YSGS在旁边围观。

规则是这样的，先给定一个正整数$m$和一个$n$个数序列$B$，一开始有一个棋子在$B$的第一个位置，并将$B_1$
减去1。此后双方轮流操作，每次操作，假设当前棋子在$i$，可以把棋子移到一个位置$j$，满足$j\in [i,min(i+m,n)]$且$B_j>0$，然后将$B_j$
​
减1，YSGH先手，谁先不能操作谁输。

众所周知，YSGH和YGSH都是绝顶聪明的，所以两人都会使用最优策略。

而隔膜使用的序列$B$是一个序列$A$的一个连续非空子序列，当然序列$A$和每次隔膜使用的序列$B$都是YSGS定的。

现在他们进行了$q$轮游戏，给出每轮游戏使用的区间，请你判断每轮谁会赢。

输入格式
由于本题数据规模较大，直接输入输出会占用比计算多数倍的时间，因此当询问过多时会对询问的输入输出进行了压缩。

第一行四个正整数$n,m,q,type$，$n,m,q$意义同题面描述，type表示当前数据的类型，type=1说明该组数据进行了压缩，type=0则说明没有，数据保证当$q>10^6$时，$type=1$。
第二行$n$个正整数，第$i$个正整数表示$a_i$，意义同题面描述。

如果$type=1$，第三行四个正整数$A,B,C,P$，表示询问的生成方式。

int A,B,C,P;
inline int rnd(){
     return A=(A*B+C)%P;}

每次询问时的调用方法为：

l=rnd()%n+1,r=rnd()%n+1;

如果生成的$l>r$，则还需要交换$l,r$。

数据保证$0<=A\ast B<P,0<=C<P,P(B+1)<2^{31}-1$

如果$type=0$，接下来$q$行，每行两个正整数$l,r$，意义同题面描述。

输出格式
输出共一行一个正整数，表示($su{m}_{i=1}^q{i}^2\ast [第i次询问YSGH会赢]mod{2}^{32}$)

$[x]$表示若$x$为真则值为$1$，否则为$0$。

输入输出样例

输入 #1

5 2 3 0
2 4 1 2 3
1 5
3 5
3 4

输出 #1

5

说明/提示
对于25%的数据：$n,m,q\le 10,A[i]\le 2$

对于55%的数据：$n,m,q\le 5000$

另有15%的数据：$n\le 10^5,m\le 5$

对于90%的数据：$n,m,q\le 10^6$

对于100%的数据：$n,m\le 10^6,q\le 10^7,1\le A[i]\le 10^9$

---

题目大意：给出一个数列，对于每个询问$[l,r]$,先手从l开始，玩家可以从左往右跳$[0,m]$格，且跳到的格子不为0（由于数列元素都大于1，其实就是不能在原地待到它变成负数），并给跳到的格子上的数字-1，谁不能跳了谁就输了，询问先手是否有必胜策略。

---

先BB一下：基础博弈练习题??? 这……

---

再BB一下：你看我多久没有写过题解了，可见这道题给我带来的震撼

---

我们开始曰一下切掉这道题的心路历程：

首先，它作为一道博弈论的题目我们自然而然要从最终最简单的情况开始讨论起：

现在轮到我了：而我站在最后一个格元素上，数字为0——啊，我必败了

现在轮到我了：而我站在最后一个格元素上，数字为1——哦，我必胜了

……

于是我们推出了这样一个结论：如果最后一个元素如果是偶数，跳上去就必败了；如果最后一个元素是奇数，跳上去就必胜了

好的，我们现在开始分类讨论：

1. 如果最后一个格子是偶数：
   
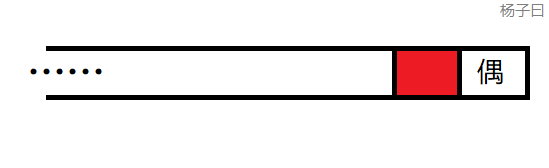
   那么，一个智商正常的人都不会往上最后一个格子跳——除非，他站在红格子上，而且红格子上的数字为0，这时他就必败了，←也就是说如果他在红格子前无路可走了，就必败，有没有发现如果我们把最后一个格子删去，将红色格子作为最后一个格子，与原问题是完全等价的，在这种情况下必败，那么原问题就必败。

2. 如果最后一个格子是奇数
   
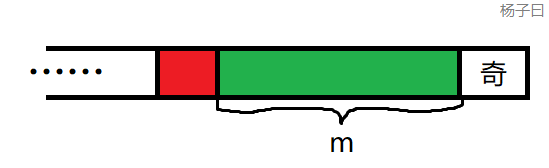
   那么有没有发现如果，我们跳到绿色格子上就必败了，因为你的对手完全可以把它跳到最后一个格子，然后根据上面的结论我们就输了，So，作为一个智商正常的人，都不会往绿色各自上跳——除非在红色格子上我们无路可走了——我们就不得不跳到一个绿色格子上。如果我们把绿色部分之后的全部删去，把红色格子作为最后一个格子，那么依然与原问题等价。

总结一波：我们从后往前考虑每个格子的奇偶性：

如果这个格子是偶数那么跳到这个格子上就是必败态，如果这个格子是奇数，那么跳到这个格子上我们就必胜了，跳到它前面的m个格子我们就必败了，然后继续考虑从这个奇数格子往前数（m+1）个的格子。

对于每一个询问，我们从终点往前模拟，得到了该询问区间内每个格子的胜负状态，答案如何判断涅？

我们可以这样想：先手从左端点出发，就相当于后手先跳到了左边第一个格子，So，我们得到第一个格子的状态，也就是后手的胜负状态取个反就欧了。

#include
using namespace std;

const int maxn=1000006;

int a[maxn],cnt[maxn];

int n,m,q,type;

int query(int l,int r){
     
	if (l>r) swap(l,r);
	int pos=r;
	for(;;){
     
		pos-=cnt[pos];
		if (pos==l) return 0;
		if (pos<l) return 1;
		pos-=m+1;
	}
	return 1;
}

int A,B,C,P;
inline int rnd(){
     return A=(A*B+C)%P;}

int main(){
     
	scanf("%d%d%d%d",&n,&m,&q,&type);
	for (int i=1;i<=n;i++) scanf("%d",&a[i]);
	for (int i=1;i<=n;i++){
     
		if (a[i]%2==1) cnt[i]=0;
		else cnt[i]=cnt[i-1]+1;
	}
	long long ans=0;
	if (!type){
     
		for (int i=1;i<=q;i++){
     
			int l,r;
			scanf("%d%d",&l,&r);
			if (query(l,r)) (ans+=1ll*i*i)%=(1ll<<32);
		}
	}
	else{
     
		scanf("%d%d%d%d",&A,&B,&C,&P);
		for (int i=1;i<=q;i++){
     
			int l=rnd()%n+1,r=rnd()%n+1;
			if (query(l,r)) (ans+=1ll*i*i)%=(1ll<<32);
		}
	}
	cout<<ans;
	return 0;
}

妙啊，复杂度是——O(qn)!!!

哦，55分了，我们开始优化：

---

如果左端点是偶数，后手一定必败（因为只有奇数的格子才有可能必胜），这种情况就不需要讨论了

如果左端点是奇数，那我们就要看这个奇数有没有被其他的奇数覆盖成后手必败态，我们不能从结尾开始模拟，So，我们考虑建一棵：

对于某一个奇数：我们让这个奇数和在这个奇数左边第一个不会被它覆盖的奇数之间连一条边，让这个奇数成为它左边奇数的儿子，如果某个奇数左边没有不会被他覆盖的奇数了，那我们就让他成为0的儿子。

于是乎，就出现了一个很显然的事情，一条从根节点到叶子节点的路径上的奇数，是不会被覆盖的，如果一个节点不会被另一个节点覆盖，那么他们之间必定是祖先关系。

总结一波：对于堆询问$[l,r]$如果左端点是偶数，先手直接必胜；如果左端点是奇数，我们就看右端点左边第一个奇数和左端点在树上是不是祖先关系就欧了！（如果是祖先关系先手必败，否则先手必胜）

那么祖先关系如何判断捏？——时间戳

也就是记录树上每个节点入栈和出栈的时间，看着两个节点的出入栈时间是否是包含关系就欧了！

OK，完事

---

c++代码：

#include
using namespace std;

const int maxn=1000005;

struct Edge{
     
	int next,to;
}edge[maxn*2];

int n,m,q,type,cnt,nedge=0;
int head[maxn],a[maxn],pre[maxn],tin[maxn],tout[maxn];

int A,B,C,P;
inline int rnd(){
     return A=(A*B+C)%P;}

void addedge(int a,int b){
     
	edge[nedge].next=head[a];
	edge[nedge].to=b;
	head[a]=nedge++;
}

void dfs(int u,int fa){
     
	tin[u]=++cnt;
	for (int i=head[u];i!=-1;i=edge[i].next){
     
		int v=edge[i].to;
		if (v==fa) continue;
		dfs(v,u);
	}
	tout[u]=cnt;
}

int query(int l,int r){
     
	if (l>r) swap(l,r);
	if (a[l]%2==0) return 1;
	r=pre[r];
	return !(tin[l]<=tin[r] && tout[l]>=tout[r]); 
}

int main(){
     
	memset(head,-1,sizeof(head));
	scanf("%d%d%d%d",&n,&m,&q,&type);
	for (int i=1;i<=n;i++) scanf("%d",&a[i]);
	for (int i=1;i<=n;i++){
     
		if (a[i]%2==1) pre[i]=i;
		else pre[i]=pre[i-1];//pre[i]表示i前第一个奇数
	} 
	for (int i=1;i<=m;i++){
     
		if(a[i]%2==0)continue;
		addedge(0,i);
	}
	for (int i=m+1;i<=n;i++){
     
		if (a[i]%2==0) continue;
		addedge(pre[i-m-1],i);
	}
	dfs(0,0);
	long long ans=0;
	if (!type){
     
		for (int i=1;i<=q;i++){
     
			int l,r;
			scanf("%d%d",&l,&r);
			if (query(l,r)) (ans+=1ll*i*i)%=(1ll<<32);
		}
	}
	else{
     
		scanf("%d%d%d%d",&A,&B,&C,&P);
		for (int i=1;i<=q;i++){
     
			int l=rnd()%n+1,r=rnd()%n+1;
			if (query(l,r)) (ans+=1ll*i*i)%=(1ll<<32);
		}
	}
	cout<<ans;
	return 0;
}

于HG机房