谈谈最近公共祖先(LCA)——杨子曰算法
谈谈最近公共祖先(LCA倍增)——杨子曰算法
今天,杨子来曰(yue)一曰(yue)算法——倍增求LCA
LCA是神马呢?
举个例子,我姓杨,你也姓杨,所以我们早在5325年前肯定有一个公共祖先,BUT这个公共祖先的儿子也有可能是我们公共的祖先,对吧?So,肯定在我们的所有公共祖先中,有一个是离我们最近的(也就是说,他的两个儿子分别是我和你的祖先),那么这个祖先就称为,我和你的最近公共祖先,即LCA.
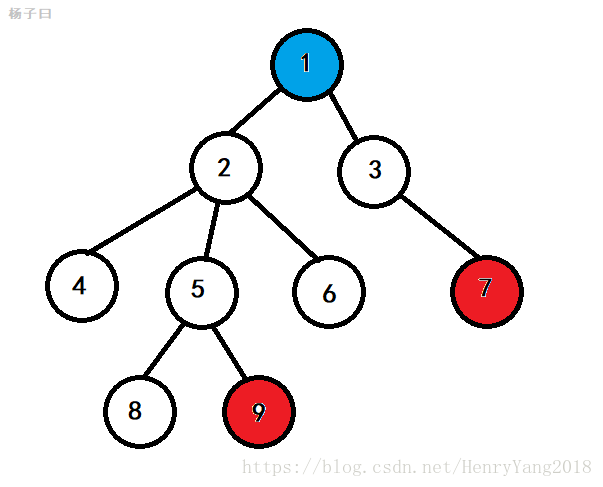
现在,我们把他放在一棵树上就很好理解了,Look at the图:
如图:结点6和结点8的LCA就是2
再看:
但如果是这样呢?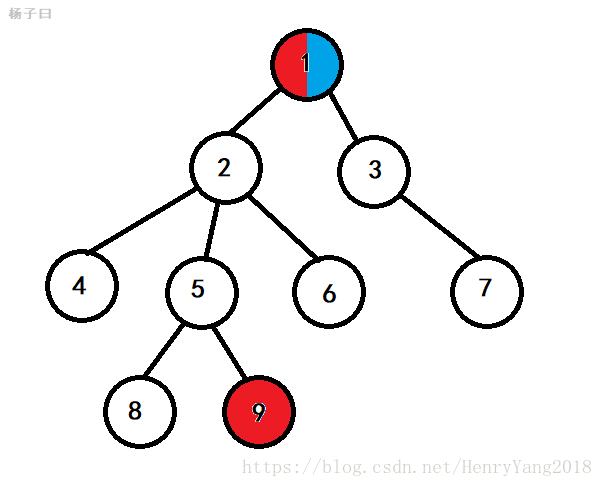
没错,结点1和结点9的LCA就是结点1,So,杨子曰:如果两个结点是爹和娃的关系,那么它们的LCA就是爹
好了,BB了半天,看出来点什么呢?或者问,我们为什么要研究LCA呢?
来看一看两点间的路径,你可以得到一个结论,杨子曰:树上两点间的路径必定经过他们的LCA
So,杨子再曰:有关两点间路径的问题,立刻想到LCA(也有可能是树链剖分)
呱呱了半天,LCA到底怎么求呢?——三个算法,今天就曰一个——倍增
(可以先看一下:ST表——杨子曰数据结构,有助于理解)
首先,我们需要一个数组f[i][j],表示结点i的第2^j个父亲是谁,那f怎样更新呢?
首先f数组全附成根节点(原因后面自然就知道了)f[i][0]可以用一次dfs全部求出,然后会发现f[i][j]就等于f[f[i][j-1]][j-1],也就是结点i的第2^ j的父亲就是i的第2^ (j-1)父亲的第2^(j-1)父亲
注意i,j循环的顺序:
for (int j=1;j<=18;j<=++){
for (int i=1;i<=n;i++){
f[i][j]=f[f[i][j-1]][j-1];
}
}
OK,这个求完了再怎么搞呢?
下面,我们假设要求x,y两个点的LCA
- 判断两点是否是父子关系
如果两点是父子关系,那么输出父亲;
等等等等,举手提问:这怎么判断?
使用dfs序-时间戳,不知道的人自行百度
简单的说就是对树dfs的时候记录进入的时间和出来的时间
判断两个结点的时间戳 是否是包含关系,就可以了 - 把 j从大到小递减,判断f[x][j]是否是y的祖先
又有人举起手说,这怎么判断,
杨子曰:请你看看上面,你是鱼的记忆吗??
使用时间戳时间戳时间戳 - 如果是就继续减小j,否则把结点x调到结点f[x][j]
如果x第2^ j个祖先也是y的祖先,那么LCA肯定是这个结点,或者是他下面的结点,所以我们减小j,如果突然发现x第2^ j个祖先不是y的祖先,呀呀呀!出大事了,现在我们无法在控制LCA的范围了,所以着急的x赶紧往上跳,调到x第2^j个祖先(下面解释为神马可以这样做)
4.j减小到0后,f[x][0]就是LCA
解释下为什么,首先要知道,一个数是可以换成几个不同的2的幂的和的形式:
如 7=1+2+4 54=2+4+16+32 (←其实就是换成2进制)
好,既然这样,那我们就可以利用这一特点,对x的祖先经行二分检索(减小j),对于LCA是x的第几个祖先也可以变成这样的形式,所谓x往上跳,就是在处理这些2^j的加数,
好,既然这样LCA就被完美实现了
总结一波:先dfs求f[i][0]和时间戳,递推求出f[i][j],对于每个询问单独判断,时间复杂度:O(n log n)
如果你还知道神马是树链剖分的话(不知道,戳我),你就可以用树链剖分求LCA(←它比倍增更快更优)
OK,完事
c++代码:
#include推荐一道题:【codevs3305】水果姐逛水果街Ⅱ
于TJQ高层小区
未经作者允许,严禁转载:https://blog.csdn.net/henryyang2018/article/details/79692080