【POJ1733】Parity game——杨子曰题目

【POJ1733】Parity game——杨子曰题目

Now and then you play the following game with your friend. Your friend writes down a sequence consisting of zeroes and ones. You choose a continuous subsequence (for example the subsequence from the third to the fifth digit inclusively) and ask him, whether this subsequence contains even or odd number of ones. Your friend answers your question and you can ask him about another subsequence and so on. Your task is to guess the entire sequence of numbers.

You suspect some of your friend’s answers may not be correct and you want to convict him of falsehood. Thus you have decided to write a program to help you in this matter. The program will receive a series of your questions together with the answers you have received from your friend. The aim of this program is to find the first answer which is provably wrong, i.e. that there exists a sequence satisfying answers to all the previous questions, but no such sequence satisfies this answer.
Input
The first line of input contains one number, which is the length of the sequence of zeroes and ones. This length is less or equal to 1000000000. In the second line, there is one positive integer which is the number of questions asked and answers to them. The number of questions and answers is less or equal to 5000. The remaining lines specify questions and answers. Each line contains one question and the answer to this question: two integers (the position of the first and last digit in the chosen subsequence) and one word which is either even' orodd’ (the answer, i.e. the parity of the number of ones in the chosen subsequence, where even' means an even number of ones andodd’ means an odd number).
Output
There is only one line in output containing one integer X. Number X says that there exists a sequence of zeroes and ones satisfying first X parity conditions, but there exists none satisfying X+1 conditions. If there exists a sequence of zeroes and ones satisfying all the given conditions, then number X should be the number of all the questions asked.
Sample Input

10
5
1 2 even
3 4 odd
5 6 even
1 6 even
7 10 odd

Sample Output

3

---

简单描述一下题意：就是你和你的朋友在玩游戏，他想了一个01序列，然后你按顺序给他一些询问对于每个询问x,y，它会回答你这个01序列的区间[x,y]里有奇数个1还是偶数个1，但是机智的你发现他在撒谎，让你输出他在回答第几个问题时撒了谎 -1（别问我为什么要-1）

---

这是一道有趣的并查集题，我们解决这道题的数据结构叫做——带权并查集（想要了解他它还有一道好题：[NOI2002]银河英雄传说）

首先，我们能不能转换一下回答的意思，如果我们记录这个01串的前缀和是sum[i]

那么回答区间[l,r]是偶数，也就是sum[y]-sum[x-1]是偶数，是不是就是告诉你：sum[x-1]和sum[y]的奇偶性相同
同样的，如果回答区间[x,y]是奇数，就相当于告诉你：sum[x-1]和sum[y]的奇偶性不同

然后我们要看的就是这一些回答中有没有矛盾，有没有发现就是并查集可以干的事情，美滋滋！
我们把奇偶性相同的放在一个并查集里，然后遇到奇偶性不同的情况判断一下是不是不在同一个并查集里就好了！完美！

BUT，有一个严重的事情：就是这道题有一堆恶心的传递性质：

1. 若$x_1$与$x_2$奇偶性相同，$x_2$与$x_3$奇偶性也相同，那么$x_1$与$x_3$奇偶性相同。（不过这种情况用上面的方式是可以维护的）
2. 若$x_1$与$x_2$奇偶性相同，$x_2$与$x_3$奇偶性不同，那么$x_1$与$x_3$奇偶性不同。（这种情况用上面的方式就不行了吧！！( •̀ ω •́ )✧）
3. 若$x_1$与$x_2$奇偶性不同，$x_2$与$x_3$奇偶性也不同，那么$x_1$与$x_3$奇偶性相同。（这种情况也不行吧！）

---

So，我们就要来用一个nb的数据结构来维护它们——带权并查集

我们不管给的两个数奇偶性是否相同，都要把并查集合并：

我们在并查集的节点i上记录一个d[i]，如果d[i]是1说明它和fa[i]的奇偶性相同，如果d[i]是0，则说明它和fa[i]奇偶性相同

第一种情况：如果x和y在同一个集合内，我们就可以通过d[x] xor d[y]可以确定x和y的奇偶性是否相同（如果是1则说明不同，如果是0则说明相同）

为什么捏，假设现在这个并查集长这样：

（我们把d[i]记在i上面那条边上，更加形象一点）

现在这张图还是没有经行路径压缩的，我们要先对x和y这两条路径压缩一下，那么压缩以后这个d[i]怎么计算捏？

先把结论告诉大家：

相信机智的你也一定发现了，压缩后的d[i]，就是一路压缩上去的d[i]的异或和

原因也非常简单：我们考虑某两个点的奇偶性是否相同，比如a和b，它们都与c相连，那么a，b，c之间的关系也就满足里上面写的传递性质，有没有发现刚好是d[a],d[b]异或的关系，那么任意两个点的关系就可把它们路径上的点两两算出（有点类似数学归纳法），就是这条路径上的异或和

int gf(int x){
    if (x==fa[x]) return x;
    int tmp=gf(fa[x]);
    d[x]^=d[fa[x]];
    return fa[x]=tmp;
}

因为x和y在同一集合，在路径压缩后fa[x]就等于fa[y]。x，y的奇偶性就可以通过上面的结论得到

得到x和y的奇偶性是否相同后和给出的答案比较一下，看看有没有矛盾就行了

int check(int x,int y,int k){
    int fx=gf(x),fy=gf(y);
    if (fx==fy){
        if ((d[x]^d[y])!=k) return 0;
    }
    else merge(x,y,k);//这是我们在下面要讨论的第二中情况
    return 1;
}

---

第二种情况：x，y如果不在同一集合怎么办

如果x和y不在同一集合，说明在此之前，x和y一点关系也没有，这时是不可能出现矛盾的情况的，那我们就要考虑一下合并怎么办了

比方说我们已经路径压缩好了：

然后我们开始合并，我们不妨把fx的爸爸变成fy：

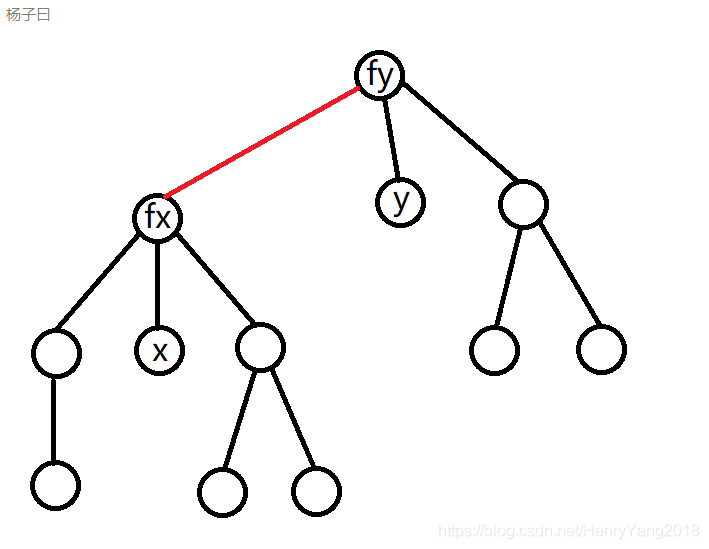
那我们现在就需要考虑一下d[fx]也就是这条红色边的d值怎么算

首先我们已经知道x，y的奇偶性关系，我们还知道它们的奇偶性关系是可以通过路径上的异或和算出的，于是我们就可以列出一个方程了(ans是x和y的奇偶性关系)：
$$ans=d[x]xord[y]xord[fx]$$

我们就美滋滋地得到了：$d[fx]=d[x]xord[y]xorans$

然后我们就可以合并了

void merge(int x,int y,int k){
    int fx=gf(x),fy=gf(y);
    fa[fx]=fy;
    d[fx]=d[x]^d[y]^k;
}

OK，完事

---

c++代码：

#include
using namespace std;

const int maxn=10005;

map<int,int> mp;

int fa[maxn*2],d[maxn*2],x[maxn],y[maxn];

char ch[maxn][10];

int gf(int x){
    if (x==fa[x]) return x;
    int tmp=gf(fa[x]);
    d[x]^=d[fa[x]];
    return fa[x]=tmp;
}

void merge(int x,int y,int k){
    int fx=gf(x),fy=gf(y);
    fa[fx]=fy;
    d[fx]=d[x]^d[y]^k;
}

int check(int x,int y,int k){
    int fx=gf(x),fy=gf(y);
    if (fx==fy){
        if ((d[x]^d[y])!=k) return 0;
    }
    else merge(x,y,k);
    return 1;
}

int main(){
    int n,m,cnt=0;
    scanf("%d%d",&n,&m);
    for (int i=1;i<=2*m;i++){
        fa[i]=i;
    }
    for (int i=1;i<=m;i++){
        scanf("%d%d%s",&x[i],&y[i],ch[i]);
    }
    for (int i=1;i<=m;i++){
        if (!mp[x[i]-1]) mp[x[i]-1]=++cnt;
        if (!mp[y[i]]) mp[y[i]]=++cnt;
        if (ch[i][0]=='e'){
            if(!check(mp[x[i]-1],mp[y[i]],0)){
                printf("%d",i-1);
                return 0;
            } 
        } 
        else{
            if(!check(mp[x[i]-1],mp[y[i]],1)){
                printf("%d",i-1);
                return 0;
            } 
        } 
    }
    printf("%d",m);
    return 0;
}

参考：

《算法竞赛进阶指南》 李煜东 著

于HG机房&TJQ高层小区