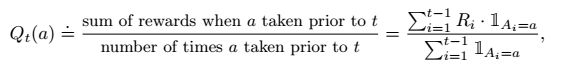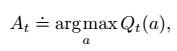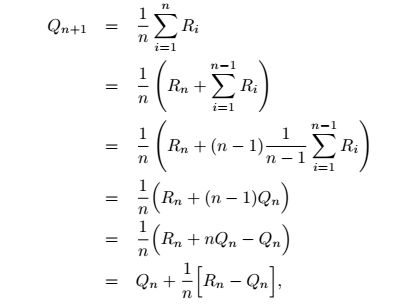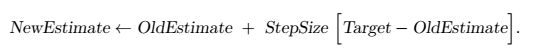【强化学习1.0】导论 & 多臂赌博机问题(multi-armed bandit)
首发于知乎:【强化学习1.0】导论 & 多臂赌博机问题(multi-armed bandit)
欢迎关注
导论:何为强化学习?
强化学习(Reinforcement Learning,下面简称RL)研究的是在交互中学习的方式。通俗来说,就是“做什么能让我们最终的收益最大化”。最常举例的一个场景就是游戏,比如下棋。对于每一步都没有标准答案可供学习,但是最终的收益是固定的,比如胜一场1分、平0分、负一场-1分。因此,一个训练有素的智能体(agent)应该能够总结经验,从而在每一步骤都向着最终取胜而行动。这就是强化学习的基本目标。
强化学习和我们所了解的有监督(Supervised)和无监督(Unsupervised)学习方法都不同。有监督的方法有标准答案(标注),而强化学习则没有一个确切的标注,只能通过环境的反馈和不断的试错来学习。
比如说,对于一个object detection来说,每个object class都有很多已经被框好的图像,因此经过训练后,model就可以识别出这个class。但是对于RL来说,我们无法对每个情境下给出一个最优的和代表性的动作予以学习。比如说,仍以下棋为例,我们并不会告诉agent在某个棋局情况下,某一步是最好的。虽然没有这种标注,但是有最终的收益(胜负)可以供agent进行总结和学习。
但是,又不能说RL是一种无监督学习,为什么?因为所谓的无监督学习,实际上是找到数据的某种隐含结构。比如,k-means试图找到所有的数据中有哪几种具有特征相似性的类别(cluster)。而对于RL来说,我们的目的并非如此,RL的目的不是对数据进行分析,找出代表性的结构,而是找到一种方式,最大化某个收益。因此,RL是有监督和无监督之外的一种新型的领域。
强化学习的重要特点有两个:1. 与不确定环境交互。2. 目标导向。这两点在RL中被作为一个整体进行考虑,即在于环境交互的过程中,达到最终的目标。
RL之所以被很多人看好,一个很直接的原因就是,这种方式像极了我们人类的智力发展以及日常做决策的过程。强化学习擅长处理的问题是各类“游戏”,其实,我们日常生活中遇到的很多问题都可以视为某种“游戏”。比如,股票投资,在何时买入、何时抛出、买入多少?这个任务可以看做是一种游戏,即我们需要对当前股票情况做判断,给出行动(action),然后环境变化,重新进行决策,再继续行动……最终衡量我们游戏的成功或者失败的,就是最终的盈亏。如果大赚一笔,自然需要总结经验,如果被割了韭菜,则需要总结教训。推而广之,生活中的各类事情,莫不如此,因此强化学习自然具有很广泛的应用价值。
强化学习的要素有:
-
策略(Policy)
-
收益信号(Reward Signal)
-
价值函数(Value Function)
-
模型(Model) (这个可以没有)
下面对上面这几个依次解释。
首先,所谓策略policy,指的是在某个场景下,agent要采取什么样的对策或行为。所以,policy决定了智能体的实际的动作,因此是RL的核心。策略比较优秀的agent能够获得更好的结果,而策略不够好的,则最终结果也不好。
policy类似于心理学中的“刺激-反应”的规则,因此,它本质上是从环境这个变量到动作这个变量的一个映射。即 s → a,s是state,即当前状态,a是action,即采取的行动。
还是拿一个真正的智能体举例。如果我们的agent是一只兔子,环境变量如果是 {有萝卜} ,那么兔子的行为就是 {停下来吃},而如果环境变量变成了 {有猎枪},那么兔子的行为相应的应该为 {逃跑}。这是一个最简单的映射,即一个lookup table就可以表示。基于这样的策略,兔子可以获得最终的比较好的收益,就是活命和成长。反之,如果策略不对,当遇到萝卜逃跑,遇到猎枪停下来,那么就会得到不好的收益,即被打死或者被饿死。因此,policy是一个agent的核心,决定了agent的性能。
接下来是收益信号 reward。收益信号指的是,在状态s下,采取了某个action后,agent获得的一个激励信号。收益信号表示的是在短时间内什么是更好的,什么是不好的。注意,这里说的是短时间内。虽然短时间的收益可以辅助我们判断action好不好,但是,我们最终的目的不是当前的收益最好,而是长远来看的总收益最高。
继续举例:我们都听说过一个实验,即延迟满足实验。对于一个小孩,发给他一颗糖,如果他吃掉,就只有这一颗,而如果等15分钟再吃,就可以再得到一颗。这里,当得到一颗糖后就吃掉,当前的收益(即快乐的感觉)增加了,但是这样也就使得最终总体的收益变少(只有+1),而如果action为不吃,那么最终的收益就是+2。通过这个例子,我们可以看出短期收益和长期收益的区别。因此,我们不能只看reward,而是还要有一种方法来评估最终的长远收益。这个评估指标就是 价值函数 value function。
价值函数 value function 在强化学习中只一个重要的概念。它表示的是对某个状态s的长远收益的评估。比如前面的例子。对于 {吃糖果} 这个action后的状态 {不再有新糖果},其value就是 0,而对于{不吃糖果} 后转移到的状态 {20min后还有糖果},其value就是+2(不考虑时间折扣的话)。价值函数是状态的函数,记做 V(s) 。它是从当前状态开始,往后继续进行下去,将来积累的所有reward的一个期望。因此,value function和reward是有联系的。所谓长远收益,其实也就是对在该状态所有可能的未来(采取不同action,转移到不同state)的reward的总和的期望。
多臂赌博机问题(multi-armed bandit)
多臂赌博机是一个经典的问题。通常用来作为RL的入门级demo。所谓的k-armed bandit指的是这样一个任务:在你面前有一个类似老虎机的k个手柄的游戏机,每次选择并拉一个手柄,就会得到一个数值(可能是奖金金额),这个金额是一个随机数,它的分布对于每个手柄都是不同的,而你的任务就是在某段时间内获得尽可能多的奖金。
一开始,我们对这个机器那个arm上的钱更多是没有任何了解的。但是,我们仍然有办法处理这个问题。那就是有策略的去试探,收集一些实验结果,并用已经有的结果推测哪个更好,然后继续实验。这个很容易理解,通过一定次数的实验,我们可以获得一定的样本,从而对每个arm的分值分布有一个推测,然后,利用这些已知的经验,去改变我们的选择arm的策略,以求最终达到最优。
下面我们用数学的方法来说明这个问题。
首先,我们要明确这个任务的目标是神马。先看下面这个公式:
这里,a代表action,即选择一个bandit,q star (a) 这个函数,一看带了star,就知道这是一个optimal最优值。那么这个最优值是怎么定义的呢?这个值表示在给定了t step时的动作a时,Rt,即t时刻的reward的数学期望。虽然里面有数学期望E,有At有Rt这些乱七八糟的符号,但其实本质上,这个公式告诉我们,我们要找到action,就是能在t时刻给我们带来最多的奖金的那个bandit。
如果每个动作的value我们都知道,那么自然可以直接选择value最高的。但是我们前面说了,首先,value是不知道的,其次,value不是一个固定的数值,而是一个分布(假如是固定数值,那我们将k个bandit都试一遍,然后一直拉那个奖金最多的杆子就行了,也没有这么复杂的问题)。这时候要怎么办呢?
这种情况就要求我们通过一定的trial来得到一组数据,以此作为经验,来估计每个动作的价值。一种最简单的方法就是,在t step之前,我们统计执行某个动作a的次数,以及执行动作a所获得的reward R 的总和,然后一平均,就知道每个动作的收益的均值了。这个也很朴素和直观,写成公式的形式,就是这样的:
根据统计学的原理,只要次数多,这么做肯定就能收敛到上面的最优的q star。这个方法被称为 采样平均方法(sample-average)。这是一种动作-价值估计方法,action-value。因为这个问题还不涉及state,即当前状态的影响。每个步骤都是独立的,这一次拉第i个bandit得到的奖励不会因为之前的动作有所变化,仍然是从第i个分布里随机取值。
现在我们有了value的估值,下一步就是利用每个bandit的value来选择如何操作。
最简单的就是所谓的贪心法(greedy),即我们每次都选那个价值最高的。也就是:
但是这种情况有个问题,因为我们说了,a只是在当前统计意义上,或者说在期望层面上是回报最大的,但是有没有可能在某个情况下,其他的action会有更好的效果呢?这个是有可能的。因此,我们采用一种叫做 epsilon-greedy的方法,来进行动作选择。
在epsilon-greedy中,我们在每个action的时候,都以epsilon(epsilon<1)的概率随机选择一个action,而1-epsilon的概率仍然是用greedy的方法,选择最高value的那个action。我们看下面这个情况,就能明白了。
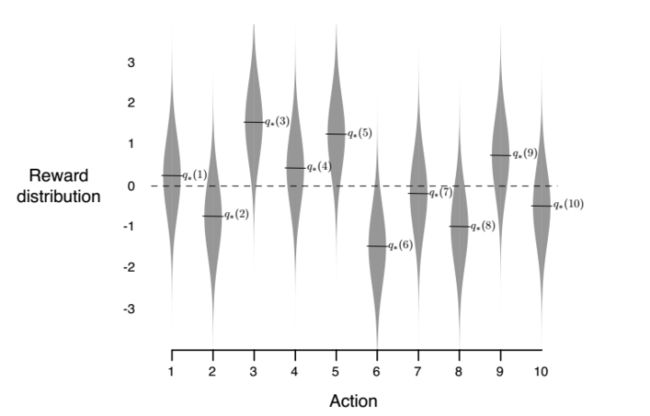
这里是一个10-armed bandit,可以看出每个bandit上的取值都是一个标准正态分布。由于我们对于期望的计算是通过已经发生的action-value数据来计算的,因此在刚开始的时候,由于样本量少,肯定有不准确的情况,也就是说,当前的value最大的,不一定就是真正value最大的那个,有可能是个次优的。而通过epsilon的概率去随机选择, 可以缓和这一情况。这里,我们将利用最优解的greedy的做法叫做exploitation,而随机选择的方法叫做exploitation。
这里就有一个问题了,那么什么情况下我们需要更多的exploitation,而什么情况下需要更多exploitation?我们设想,如果reward的方差比较大,或者有噪声、非平稳等等情况下,由于要找到最优解更加困难,所以需要多次exploration,即探索。反之,如果reward分布比较稳定,且方差较小,就更应该偏重exploitation。举个极端的例子,如果方差为0,那么一次遍历就搞定了,然后不停取最大的reward即可。这是上面说到过的。
还有一个重要的点,叫做增量式实现。如下:
这里,R代表每次的reward,由于Q就是一个均值,所以,n+1时刻的Qn+1,可以用Qn和新进来的Rn进行计算。这个推导其实很简单。为啥要这样做呢?因为,我们需要一个可以时序第更新的方法,新来一次reward,就能将Q更新一次,而且不用把之前所有的都进行保存,只保存上一个时刻的平均值即可。这个小trick在很多地方是挺常用的,比如图像均值滤波中的一种优化算法就是这样的,可以减少运算量。
这个增量式方法还可以写成一个更通用的形式:
reference:
-
Reinforcement Learning: An Introduction, by Sutton, R.S. and Barto
-
https://github.com/zhoubolei/introRL