统计建模-多元线性回归预测房价
简单聊聊统计建模中,使用多元线性回归模型来预测房价。
文章目录
-
- 变量描述:
- (1)读取数据
- (2)单变量描述
- (3)自变量对因变量的影响分析
- (4)检验变量重要性
- (5)筛选出重要变量建模
- (6)模型检验,也就是残差检验
- (7)模型调优
- (8)总结
变量描述:
price是被解释变量,其余的变量是解释变量。
dist-所在区
roomnum-室的数量
halls-厅的数量
AREA-房屋面积
floor-楼层
subway-是否临近地铁
school-是否学区房
price-平米单价
(1)读取数据
使用shape函数看数据有多少行,多少列;describe函数看各指标数据的分布情况;使用info函数查看变量的是否存在缺失值和变量的数据类型,如果存在缺失值看是否需要进行填充。
import pandas as pd
import numpy as np
import os
import matplotlib as mat
import matplotlib.pyplot as plt
import seaborn as sns
import statsmodels.api as sm
from statsmodels.formula.api import ols
# 读取数据,熟悉理解数据的含义,一个小时
raw_data = pd.read_csv('sndHsPr.csv')
print(raw_data.head())
# --------------------------------------
'''查看原始数据的分布情况,如果有需要,需要对缺失值异常值进行处理'''
raw_num, columns_num= raw_data.shape
print('数据集的大小:', raw_data.shape)
# 描述性统计,一般看均值,最小最大值和中位数,看看是否存在异常值
describ_data = raw_data.describe()
print("数据集的描述分布:", raw_data.describe().T)
# 数据类型和缺失值统计,没有缺失值
print("数据集的信息分布:", raw_data.info())
(2)单变量描述
1、连续变量
通过看连续变量分布可以发现数据的偏态和异常值的情况。
制直方图,看数据的偏度情况(hist绘制直方图);另外还需要看变量的最小、最大、均值、中位数、标准差等这些指标的分布情况(使用agg函数)。
# 连续变量看分布,集中和离散程度,右偏,y也是右偏,可以取对数
raw_data['AREA'].hist(bins = 20)
raw_data['AREA'].agg(['min', 'max', 'mean', 'median', 'std'])
2、离散变量
离散变量通过看频数,占比可以发现数据均衡性问题;
print(pd.DataFrame(raw_data[var].value_counts()).T)
(3)自变量对因变量的影响分析
其实可以根据这个影响程度,大致判断出建模所需要的重要变量、次要变量和无关变量。但是在统计建模中这样粗糙的来进行判断其实是不专业的,那么怎么办呢,对于大样本数据集而言,可以用抽样的方法,再使用统计检验的方式来检验变量重要性。
离散对离散:使用柱形图看差异,卡方检验
离散对连续:使用箱线图,看中位数是否存在差异,方差分析或T检验
连续对连续:散点图,看相关系数
离散对连续,使用boxplot绘制箱线图,看离散自变量与连续因变量之间的关系。
# 字符中文显示
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号
# 离散自变量和因变量之间的关系,T检验和方差分析就,使用箱线图
for j in range(len(conti_var)):
print('变量是:', conti_var[j])
# raw_data[conti_var[j]] = raw_data[conti_var[j]].astype('category')
sns.boxplot(x = conti_var[j], y = 'price', data = raw_data)
plt.show()
连续对连续,使用scatter绘制散点图,看连续自变量与连续因变量之间的关系:
plt.scatter(raw_data['AREA'], raw_data['price'])
print('连续变量之间的相关系数', raw_data['AREA'].corr(raw_data['price']))
(4)检验变量重要性
1、数据抽样
为什么要对数据进行抽样呢,因为在统计学上来说,样本量太大的话P值就失去了意义,所以统计建模的话,样本量不宜过大,因此需要对样本进行抽样,来参与建模。
def get_sample(df, sampling="simple_random", k=1, stratified_col=None):
"""
对输入的 dataframe 进行抽样的函数
参数:
- df: 输入的数据框 pandas.dataframe 对象
- sampling:抽样方法 str
可选值有 ["simple_random", "stratified", "systematic"]
按顺序分别为: 简单随机抽样、分层抽样、系统抽样
- k: 抽样个数或抽样比例 int or float
(int, 则必须大于0; float, 则必须在区间(0,1)中)
如果 0 < k < 1 , 则 k 表示抽样对于总体的比例
如果 k >= 1 , 则 k 表示抽样的个数;当为分层抽样时,代表每层的样本量
- stratified_col: 需要分层的列名的列表 list
只有在分层抽样时才生效
返回值:
pandas.dataframe 对象, 抽样结果
"""
import random
import pandas as pd
from functools import reduce
import numpy as np
import math
len_df = len(df)
if k <= 0:
raise AssertionError("k不能为负数")
elif k >= 1:
assert isinstance(k, int), "选择抽样个数时, k必须为正整数"
sample_by_n=True
if sampling is "stratified":
alln=k*df.groupby(by=stratified_col)[stratified_col[0]].count().count() # 有问题的
#alln=k*df[stratified_col].value_counts().count()
if alln >= len_df:
raise AssertionError("请确认k乘以层数不能超过总样本量")
else:
sample_by_n=False
if sampling in ("simple_random", "systematic"):
k = math.ceil(len_df * k)
#print(k)
if sampling is "simple_random":
print("使用简单随机抽样")
idx = random.sample(range(len_df), k)
res_df = df.iloc[idx,:].copy()
return res_df
elif sampling is "systematic":
print("使用系统抽样")
step = len_df // k+1 #step=len_df//k-1
start = 0 #start=0
idx = range(len_df)[start::step] #idx=range(len_df+1)[start::step]
res_df = df.iloc[idx,:].copy()
#print("k=%d,step=%d,idx=%d"%(k,step,len(idx)))
return res_df
elif sampling is "stratified":
assert stratified_col is not None, "请传入包含需要分层的列名的列表"
assert all(np.in1d(stratified_col, df.columns)), "请检查输入的列名"
grouped = df.groupby(by=stratified_col)[stratified_col[0]].count()
if sample_by_n==True:
group_k = grouped.map(lambda x:k)
else:
group_k = grouped.map(lambda x: math.ceil(x * k))
res_df = df.head(0)
for df_idx in group_k.index:
df1=df
if len(stratified_col)==1:
df1=df1[df1[stratified_col[0]]==df_idx]
else:
for i in range(len(df_idx)):
df1=df1[df1[stratified_col[i]]==df_idx[i]]
idx = random.sample(range(len(df1)), group_k[df_idx])
group_df = df1.iloc[idx,:].copy()
res_df = res_df.append(group_df)
return res_df
else:
raise AssertionError("sampling is illegal")
# 抽样,然后根据统计检验来筛选变量参与建模,实际上在建模的时候就是抽样之后的样本,其实这样也能很好的解决数据均衡性的问题
data_sample = get_sample(raw_data, sampling="stratified", k=400, stratified_col=['dist'])
# 看每个自变量对因变量的解释性,挑选出变量参与建模,离散的抽样(P值问题),
2、变量重要性检验并筛选出建模变量
根据抽样后样本的P值,来判定变量重要性,可以多抽样几次,显著的不管怎么抽还是显著,这就是重要变量;次要变量是那种P值忽高忽低的;无关变量每次抽都是不显著的。
print('dist的P值为:%.4f'%sm.stats.anova_lm(ols(formula='price~C(dist)', data=data_sample).fit())._values[0][4])
(5)筛选出重要变量建模
建模的时候,在分类变量前面加个C,就会在建模之前自动将该变量进行哑变量编码,哑变量编码和one_hot编码是有区别的,具体可以参考下面的博客:
两种编码方式的差异:https://www.cnblogs.com/lianyingteng/p/7792693.html
'''建模,可以不进行哑变量编码'''
lm1 = ols("price ~ C(dist)+school+subway+C(floor)+AREA", data = data_sample).fit()
lm1_summary = lm1.summary()
lm1_summary #回归结果展示
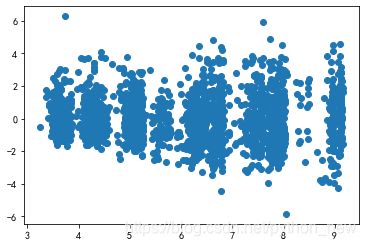
(6)模型检验,也就是残差检验
从残差图中可以看出,残差呈现发散的趋势,此时需要对模型进行调整,因为price和AREA变量都是右偏,我们取个对数看看情况。
data_sample['predict'] = lm1.predict(data_sample)
data_sample['resid1'] = lm1.resid
plt.scatter('predict', 'resid1', data = data_sample)
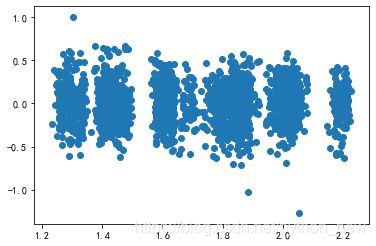
(7)模型调优
对变量取对数之后,残差趋于稳定,模型构造完成,后面可以根据自己的需要,对模型进行预测了。
# 取对数,解决异方差问题
data_sample['price_ln'] = np.log(data_sample['price'])
data_sample['AREA_ln'] = np.log(data_sample['AREA'])
# 重新建模
lm2 = ols("price_ln ~ C(dist)+school+subway+C(floor)+AREA_ln", data = data_sample).fit()
lm2_summary = lm2.summary()
lm2_summary #回归结果展示
# 存在异方差
data_sample['predict_ln'] = lm2.predict(data_sample)
data_sample['resid1_ln'] = lm2.resid
plt.scatter('predict_ln', 'resid1_ln', data = data_sample)
(8)总结
1、统计检验:在这里只是简单介绍了多元线性回归统计建模的基本流程,实际上在数据挖掘或机器学习中,统计检验那块可以省略,直接看图形来筛选变量
2、残差分析:残差分析不够全面,这里只是简单介绍了一下而已
3、共线性:没有对自变量做共线性分析
4、交互项:没有考虑重要自变量交互情况对因变量的影响
5、讨论:连续变量分布不稳定怎么办?离散变量分布不均衡怎么办?