最近做到的一些有意思的数学题目（博弈，双人玩游戏）

最近做一些数学题目，感觉挺有意思的整理了一下。

1.北京理工大学2018级3月月赛A题：Ervin and Joker

https://vjudge.net/problem/Gym-241030A#author=0

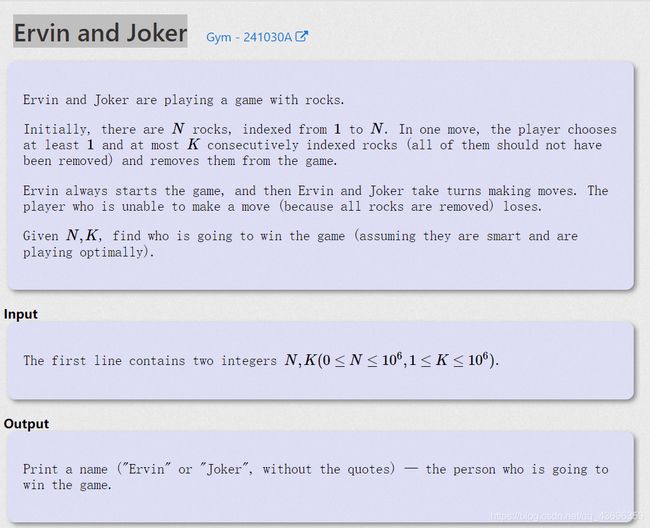
简单博弈：不难看出，只要Ervin能把中间的一个或者两个拿走使之隔开，那么Ervin必胜。
所以有以下两种情况Ervin可能会输：

#include 

using namespace std;
#define eps 1e-8
#define close ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
typedef long long ll;
const int maxn = 1e6;
const int INF = 1e9;
const ll linf = 0x3f3f3f3f3f3f3f3f;
const double PI = acos(-1.0);
ll mod = 1e9+7;
int main()
{
	int n , k;
	cin>>n>>k;
	if(n==0)cout<<"Joker"<<endl;
	else if(k==1&&n%2==0)cout<<"Joker"<<endl;
	else cout<<"Ervin"<<endl;
}

2.Codeforces Round #573 (Div. 2)D题：Tokitsukaze, CSL and Stone Game

http://codeforces.com/contest/1191/problem/D

写的时候被hack了，后来面向测试点的编程过了……

AC代码：

#include 
 
using namespace std;
typedef long long ll;
ll n,a[100086];
 
int main()
{
    cin>>n;
    ll sum=0;
    set<ll >s;
    for(int i=0;i<n;i++){
        cin>>a[i];
        sum+=a[i];
        s.insert(a[i]);
    }
    if(s.size()<=n-2){cout<<"cslnb"<<endl;exit(0);}
    sort(a,a+n);
    int kkk=0;
    
    if(n>=3)for(int i=1;i<n-1;i++)
    {
        if(a[i]==a[i+1]&&a[i-1]==a[i]-1){kkk=1;break;}
    }
    ll ans=sum-((1ll*n*(n-1))/2);
    if(kkk==1)cout<<"cslnb"<<endl;
    else if(sum==0||(a[0]==0&&a[1]==0))cout<<"cslnb"<<endl;
    else if(ans%2==0)cout<<"cslnb"<<endl;
    else cout<<"sjfnb"<<endl;
}

3.Codeforces Round #573 (Div. 2)E题：Tokitsukaze and Duel

http://codeforces.com/contest/1191/problem/E

题意：

给你一个长度为n的01字符串，和一个整数k。二人进行做博弈游戏，每个人必须选择一个连续的k个字符，把这连续的k个字符全变为0或者1。如果某次操作之后整个字符串全为1或者0，那么这个胜利，如果有无限多步要走，那么算平局，假设二人都绝顶聪明。给你初始局面，问游戏结果是什么？

思路：

首先应该明确，如果先手要赢，他一定要在第一步就赢，否则就不能再赢了。后手要赢的话，他要在他走的第一步赢，不然也不能再赢了、因为另外一个人可以重复选择他刚刚选择的区间，使其不停的翻转，可以知道这样是一直循环下去而且无意义的。

#include
using namespace std;
#define ll long long
int main()
{
	ll n,k,i=1,x=1,y=1,z;
	cin>>n>>k;
	string str;
	cin>>str;
	while(i<n && str[i]==str[0])
		i++,x++;
	i=n-2,z=n-k-1;
	while(i>=0 && str[i]==str[n-1])
		i--,y++;
	if((x+k)>=n || (y+k)>=n || (str[0]==str[n-1] && (x+y+k)>=n))
		cout<<"tokitsukaze"<<endl;
	else if(str[0]!=str[n-1] && x>=z && y>=z && k>=z)
		cout<<"quailty"<<endl;
	else
		cout<<"once again"<<endl;
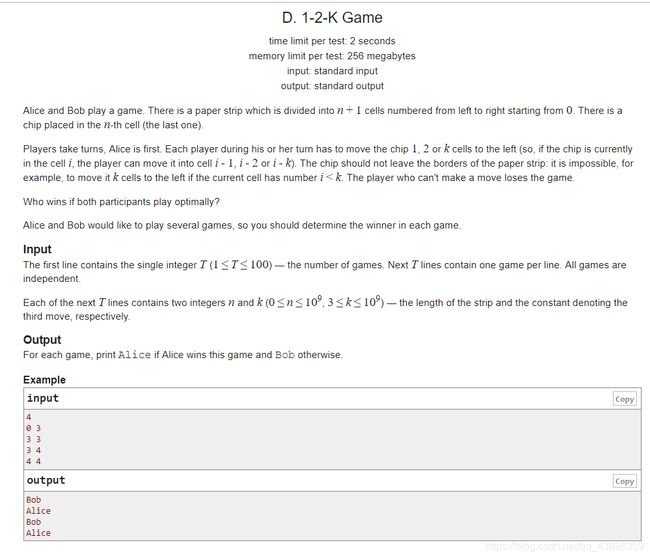
	return 0;
}

4.Educational Codeforces Round 68 (Rated for Div. 2)D. 1-2-K Game

http://codeforces.com/contest/1194/problem/D

题意：

当前在n位置，每一次可以向左走1,2，或者k步，最左的位置是0，不能走到0的左边， 二人博弈问题，谁没法再走的时候就输掉，问先手必赢还是后手必赢。

思路：

首先确定的是 0位置是必输位置，因为 1 2 和k这三个位置可以一步就走到0位置，所以这3个位置是必赢位置，以此规律，我们可以递推出sg函数。

由此我们可以打个表

#include 

using namespace std;
#define eps 1e-8
#define close ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
typedef long long ll;
const int maxn = 1e6;
const int INF = 1e9;
const ll linf = 0x3f3f3f3f3f3f3f3f;
const double PI = acos(-1.0);
ll mod = 1e9+7;
int sg[maxn];
int main()
{
	int n,k;
    n=100;
    cin>>k;
    sg[0]=0;
    sg[1]=1;
    sg[2]=1;
    for (int i = 3; i <= n; ++i)
    {
        if((i-k)>=0)
        {
            if(sg[i-1]==0||sg[i-2]==0||sg[i-k]==0)
            {
                sg[i]=1;
            }
        }else
        {
            if(sg[i-2]==0||sg[i-1]==0)
            {
                sg[i]=1;
            }
        }
    }
    for(int i = 0;i <= n; i++)
    {
        cout<<i<<" "<<sg[i]<<endl;
    }
    return 0;
}

不 难 发现:

• 如果k是3的倍数，那么sg函数是k+1长度的循环节，对循环节取模后，判断n是否是k，如果是k，那么k位置必赢，否则判断是否是3的倍数。如果k不是3的倍数，那么判断n是否是3的倍数即可。

AC代码:

#include 
 
using namespace std;
#define eps 1e-8
#define close ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
typedef long long ll;
const int maxn = 1e6;
const int INF = 1e9;
const ll linf = 0x3f3f3f3f3f3f3f3f;
const double PI = acos(-1.0);
ll mod = 1e9+7;
void solve(int n,int k){
	if(n==0){
		cout<<"Bob"<<endl;
		return ;
	}
	if(k%3!=0){
		if(n%3==0)cout<<"Bob"<<endl;
		else cout<<"Alice"<<endl;
		return ;
	}
	else {
		int ttt=n%(k+1);
		if(ttt==k||ttt%3!=0)cout<<"Alice"<<endl;
		else cout<<"Bob"<<endl;
		return ;
	}
}
int main()
{
	close;
	int T;
	cin>>T;
	while(T--)
	{
		int n,k;
		cin>>n>>k;
		solve(n,k);
	}
}	

通过打表找一下规律,可以大大节省时间

5.POJ1082Calendar Game

传送门:http://poj.org/problem?id=1082

题意:

给你一个年月日，你可以移动月和日，如果下个月没有当前的天数的时候你就不能移动月，当你刚好移动到11月4日你就赢了，如果你超过了十一月四日你就输了。

刚开始看这道题感觉可以用dfs,后来开始写代码时候感觉要判好几个条件,就没写下去,于是思考了一下,发现:

最终我们应该到达的是奇数点，即每次我们都需要保证自己走完后另一位所面对的是奇数局势，然后他只能走到偶数点，也就是一开始我们保证自己是偶数点开局就能赢。于是我就交了几发听取WA声。后来，参考了网上的题解。。
才知道，存在（9，30）这个点，下一个点还是奇数点（10,1），或者你可以直接走到（10，30），这样就是偶数点（聪明人都会选择前一种做法，让下一个人面对的局势是必败局），同样对于（11，30），你可以直接走到（12，1），这两个点也是必胜的。总结一下:只开局为偶数开局或者为（9，30），（11，30） 两个特殊的日子，就是必胜局，其他的为必败局。

AC代码:

#include 

using namespace std;
#define eps 1e-8
#define close ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
typedef long long ll;
const int maxn = 1e6;
const int INF = 1e9;
const ll linf = 0x3f3f3f3f3f3f3f3f;
const double PI = acos(-1.0);
ll mod = 1e9+7;
int main()
{
    close;
    int y,m,d;
    int T;
    cin>>T;
    while(T--)
    {
        cin>>y>>m>>d;
        if((m+d)%2==0||(d==30&&(m==9||m==11)))
            puts("YES");
        else
            puts("NO");
    }
    return 0;
}

博弈中诸如巴什博弈,威佐夫博奕,Fibonacci博弈,尼姆博弈,公平组合博弈（Impartial Combinatori Games),我觉得都挺有意思的,等过段时间我还想研究研究…