微分流形基础点备注
【参考资料】
【1】《拓扑学的基础和方法》
【2】《物理学家用微分几何》
【3】《微分几何入门与广义相对论》
一、连续性
在拓扑空间中因为没有度量的概念,因此用开集的逆像仍然是开集来定义连续性,如下举例:

备注:拓扑里的开集、闭集可以理解是实数轴开区间、闭区间的推广。
二、流形
流形定义:可分的度量空间,并且它的任意点x都有领域同胚于n维开球
O B n = { x ∣ ρ ( 0 , x ) < 1 } OB^n=\{x | \rho(0, x) < 1 \} OBn={x∣ρ(0,x)<1}的拓扑空间,记作 M n M^n Mn
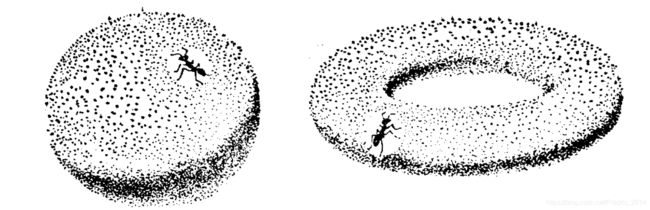
这里对于这只小蚂蚁而言,从它的视角看两者都是一个以当前点为圆心,半径为1的开圆的同胚
*另一种定义: 实(复)n维流形是一个豪斯道夫空间,它的每个点有开领域 R n ( C n ) R^n(C^n) Rn(Cn)同胚。
注意:这里同胚的n值和n维流形的n值是一样的,比如一维直线是一维流形,但两条一维直线交叉就不是,因为交叉点明显不是一维的;二维的圆盘是二维流形,但三维的圆锥表面就不是,因为在圆锥的顶点是三维的,抛开这点的其他区域可以认为二维流形。可以将流形理解成一种高维空间的连续性。
三、微分流形
2.1 对微分的定义
有函数 y = f ( x ) y=f(x) y=f(x)看做 f : R → R f:R \to R f:R→R。做数列 { ( f ( x + h n ) − f ( x ) ) / h n } \{(f(x + h_n) - f(x)) / h_n \} {(f(x+hn)−f(x))/hn},这里 h n h_n hn是收敛于0的任意数列。因此当 { ( f ( x + h n ) − f ( x ) ) / h n } \{(f(x + h_n) - f(x)) / h_n \} {(f(x+hn)−f(x))/hn}与 h n h_n hn无关的收敛到一个常数时,称f在x可微。
如果f在集合A上各个点可微,则称f在A上可微。
2.2 对坐标卡的定义
上图表示这样一个意思,在n维流形里有两个开集 U α U_{\alpha} Uα和 U β U_{\beta} Uβ,它们分别存在到R^n的映射 ϕ α \phi_{\alpha} ϕα和 ϕ β \phi_{\beta} ϕβ。
当流形M由若干个开集覆盖 ∪ α U α \cup_{\alpha}U_{\alpha} ∪αUα,并且有对应的到 R n R^n Rn的映射,则我们有流形M的坐标卡集 A = ( U α , ϕ α ) A={(U_{\alpha}, \phi_{\alpha})} A=(Uα,ϕα)
2.3 对流形的微分结构定义
微分几何是研究微分流形在微分同胚变换下的不变性质。
备注:重申一下,可微(导)必然连续,但连续不一定可微(导)
前置定义1:考虑 f : R n → R f: R^n \to R f:Rn→R的情况,我们有偏导数 ∂ f ∂ x i \dfrac{\partial f}{\partial x_i} ∂xi∂f的定义。同时也可以对其他变量求导,因此有n阶偏导数的定义 ∂ n f ∂ x 1 ∂ x 2 . . . ∂ x n \dfrac{\partial ^n f}{\partial x_1\partial x_2...\partial x_n} ∂x1∂x2...∂xn∂nf。当第n阶偏导数连续时,我们称f为 C n C^n Cn类函数。如果对于任意n都是成立的,则成为 C ∞ C^\infty C∞类函数。
前置定义2: 回到"对坐标卡的定义"章节,我们还要求 ( U α , ϕ α ) (U_{\alpha}, \phi_{\alpha}) (Uα,ϕα)和 ( U β , ϕ β ) (U_{\beta}, \phi_{\beta}) (Uβ,ϕβ)满足相容条件:
f = ϕ α . ϕ β ′ : ϕ α ( U α ∩ U β ) → ϕ β ( U α ∩ U β ) f=\phi_{\alpha}.\phi_{\beta}': \phi_{\alpha}(U_{\alpha} \cap U_{\beta}) \to \phi_{\beta}(U_{\alpha} \cap U_{\beta}) f=ϕα.ϕβ′:ϕα(Uα∩Uβ)→ϕβ(Uα∩Uβ)
备注:意味着定义了一个映射,从上图中 α \alpha α对应的 R n R^n Rn(左边的阴影)映射到上图中 β \beta β对应的 R n R^n Rn(右边的阴影)
这里的相容性要求这个映射f` C k C^k Ck类函数,称两个坐标卡 C k C^k Ck相容
定义: 当流形M上的坐标卡集 A = ( U α , ϕ α ) A={(U_{\alpha}, \phi_{\alpha})} A=(Uα,ϕα),满足如下三个条件,则称其为流形M的 C k C^k Ck微分结构:
(1) U α U_{\alpha} Uα是流形M的开覆盖
(2) A中任意两个坐标卡都是 C k C^k Ck相容
(3) A为具备上述两个特性的最大的坐标卡集
当其相容为 C ∞ C^\infty C∞时成为光滑流形。
举例(重要):
我们已知球面是一个二维流形,定义如下:
S 2 = { ( x , y , z ) ∈ R ∣ x 2 + y 2 + z 2 = 1 } S^2=\{(x,y,z)\in R|x^2 + y^2 + z^2 = 1\} S2={(x,y,z)∈R∣x2+y2+z2=1}
可以取两个开集
U + = { ( x , y , z ) ∈ S 2 ; z ≠ − 1 } U_{+}=\{(x,y,z) \in S^2 ; z \ne -1\} U+={(x,y,z)∈S2;z̸=−1},即整个球面去掉-1定点
U − = { ( x , y , z ) ∈ S 2 ; z ≠ 1 } U_{-}=\{(x,y,z) \in S^2 ; z \ne 1\} U−={(x,y,z)∈S2;z̸=1},即整个球面去掉+1定点
分别定义两个微分结构:
备注: 其实就是定义一个从M到 R 2 R^2 R2的映射
ϕ + : ( x , y , z ) → ( x 1 + z , y 1 + z ) \phi_{+}:(x,y,z) \to (\dfrac{x}{1 + z}, \dfrac{y}{1 + z}) ϕ+:(x,y,z)→(1+zx,1+zy)
ϕ − : ( x , y , z ) → ( x 1 − z , y 1 − z ) \phi_{-}:(x,y,z) \to (\dfrac{x}{1 - z}, \dfrac{y}{1 - z}) ϕ−:(x,y,z)→(1−zx,1−zy)
这个映射在几何上就是从定点z=1或-1做(x,y)的投影映射,映射到z=0的平面上。 可以证明他们是 C ∞ C^\infty C∞相容的,因此 S 2 S^2 S2是二维光滑流形。