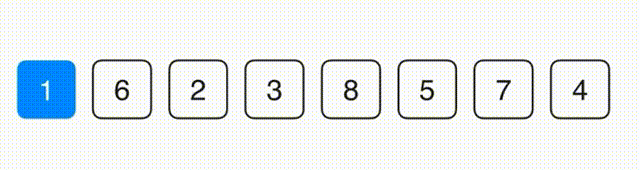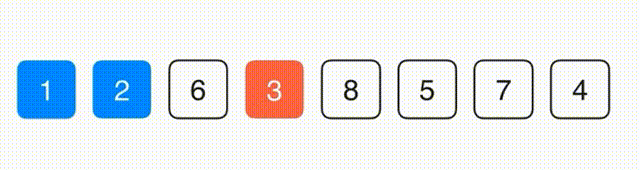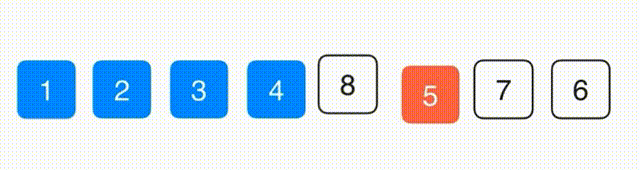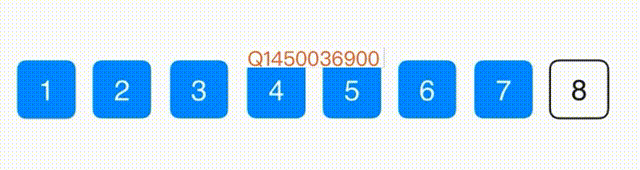快速排序 冒泡排序 希尔排序 归并排序 选择排序 插入排序 详解
选择排序
时间复杂度O(n^2) 空间复杂度O(1)
思路:找到最小的元素放到第一位,在剩下的元素中找到最小的放到第二位,以此类推
/**
选择排序算法就是通过n-i次关键字的比较,从n-i+1个记录中选出关键字最小的
记录,并和第i(1<=i<=n)个记录交换
**/
#include
void SelectSort(int k[],int n)
{
int i,j,min,temp,count1=0,count2=0;
for(i=0;i 插入排序
思路:8 6 2 3 1 5 7 4 这个数组中的元素 第一个元素8不动因为只考虑8这个元素时已经排好序了。看6这个元素,我们的目的时把6这个元素放到前面数组中合适的位置,6比8小所以交换位置,此时前两个元素排好位置了,看2这个元素,2比8小交换一次位置,2比6小再交换一次位置,此时三个元素就排好位置了 2 6 8,接下来看3这个元素,3比8小交换一次位置,3比6小交换一次位置,3比2大应该插入到2和6之间,至此,四个元素排序完成了2 3 6 8 以此类推
插入排序和选择排序相比多了一个循环的终止条件理论上比选择排序快
#include
void InsertSort(int k[],int n)
{
int i,j,temp;
//i从1开始 因为第一个元素默认有序 从第二个开始
for(i=1;i0
//j指向当前要考察元素的位置,看每一次当前位置的元素是不是比前一个还要小,如果小,就把j上的元素
和j-1上的元素交换位置 j--依次向前查看 看是不是还能和前一个元素比较以此类推
如果j位置上的元素已经大于j-1位置上的元素,说明已经放在了合适的位置了 终止循环放心去考察下一个i所代表元素的位置了
for(j=i;j>0 && k[j] 插入排序改进算法
优点:交换的本质是三次赋值 现在把交换完全通过赋值取代了性能会更优
思路:8 6 2 3 1 5 7 4对于第0个位置的元素8不变,看6这个元素,先把6复制一份保存起来,在看6是不是应该放到当前位置(方法是把6和前一个位置的8比较)6比8小说明6不应该放到这个位置8应该放到这个位置,把8向后移动一个位置,在看6是不是应该放到前一个位置,此时已经是第0个位置了,不用比较直接把6放到这个位置,6 8 排序完成,在看2这个元素,先把2复制一个副本,再来看2是不适合呆在这个位置,2比前面位置的8小所以不应该呆在这个位置,把这个位置赋值8,再看2是不是应该放到原来8这个位置,2比前一个元素6小所以将6放到这个位置,再看2是不是应该放到原来6的位置,又是第0个位置了,直接赋值就行了;再看3这个元素,先复制一个副本,再来看3是不适合呆在这个位置,3比前面位置的8小所以不应该呆在这个位置,把这个位置赋值8,再看3是不是应该放到原来8这个位置,发现3比前一个元素6小所以将6放到这个位置,再看3是不是应该放到原来6的位置,发现3比前面的2大说明3就应该放到这个位置,把这个位置赋值为3,前四个就排序完成了 2 3 6 8 依次类推
整个过程和之前的逻辑一样只不过把一次又一次的交换操作变成了比较后赋值(一次交换=3次赋值)把这么多减缓替代了所以性能更优。 插入排序对于近似有序的数组性能最优 比如系统日志
时间复杂度O(n^2) 空间复杂度O(1)
#include
void InsertSort(int k[],int n)
{
int i,j,temp;
//i从1开始 因为第一个元素默认有序 从第二个开始
for(i=1;i=0&& k[j]>temp;j--)
{
k[j+1]=k[j];//把前一个元素的位置向后移
}
k[j+1]=temp;// 符合条件插入元素
}
}
}
int main()
{
int i,a[10]={8,2,6,5,0,3,9,6,7,4};
InsertSort(a,10);
printf("排序后得结果是:\n");
for(i=0; i<10; i++)
{
printf("%d ",a[i]);
}
printf("\n\n");
} 冒泡排序
冒泡排序得要点
1 两两注意是相邻的两个元素的意思
2 如果有n个元素需要比较n-1次,每轮减少一次比较
3 既然是冒泡排序,那就是从下往上两两比较,所以看上去就跟泡泡往上冒一样
#include
void BubbleSort(int k[],int n)
{
int i,j,temp,count1=0,count2=0;
for(i=0; ik[j])
{
count2++;
temp=k[j];
k[j]=k[i];
k[i]=temp;
}
}
}
printf("总共进行了%d次比较,进行了%d次移动",count1,count2);
} 正宗冒泡排序
对 1 0 2 3 4 5 6 7 类似这样的有优势
void BubbleSort(int k[],int n)
{
int i,j,temp,count1=0,count2=0,flag;
flag=1;
for(i=0; ii; j--)
{
count1++;
flag=0;
if(k[j-1]>k[j])
{
count2++;
temp=k[j-1];
k[j-1]=k[j];
k[j]=temp;
flag=1;
}
}
}
printf("总共进行了%d次比较,进行了%d次移动",count1,count2);
}
希尔排序
时间复杂度O(n*logn)
void InsertSort(int k[],int n)
{
int i,j,temp;
int gap=n;
do
{
gap=gap/3+1;
for(i=gap;itemp&&j>=0;j-=gap)
{
k[j+gap]=k[j];
}
k[j+gap] = temp;
}
}
}while(gap>1);
} 归并排序
时间复杂度O(n*logn)
思路:首先将数组分成一半,想办法把左边数组排序,把右边数组排序,之后再将他们归并起来,在分别将左边的数组和右边的数组分成一半,然后对每一个部分先归并在排序,再把每一个部分分半归并,分到一定细度的时候就只有一个元素了,此时不用排序就是有序的,此时对他们进行归并,归并到上一个层级,逐层向上上升,归并到最后一层的时候全部有序了。
在这个过程中我们一层一层划分分成三级到第三级的时候每层只剩下一个元素了,总共有8个元素每次二分,经过三次除以2的运算,每一部分就只剩下一个元素了,也就是log2^8=3,如果我们是n个元素呢,就有logn这样的层级,如果n不是一个log2^x的表现形式,那结果可能是一个浮点数,我们只需要向上取整就好了。总之,层数是logn这样的数量级的,我们每一层要处理的元素是一样的,虽然我们把他分成了不同的部分,如果整个归并过程可以以O(n)的时间复杂度解决的话,那我们就设计出了nlogn级别的算法。事实上,这也是nlogn时间复杂度算法的来源,通常是通过二分法达到logn这样的层级,每一级用O(n)级别的算法做事情。
接下来问题是把层级划分成两部分,这两部分排好序后使用O(n)的算法将它们归并到一起形成新的有序数组。使用递归完成整个排序。我们需要开辟同样大小的临时空间来辅助我们完成归并过程,使用临时空间归并比较容易需要O(n)额外的空间来完成排序。怎样利用辅助空间将两个排序好的的数组合并成一个数组呢?用3个索引在数组中进行追踪蓝色箭头表示在归并过程中我们需要追踪的位置两个红色的箭头分别指向当前我们已经排好序的数组当前要考虑的元素1比2小首先将1放到最终数组中,蓝色的箭头考虑下一个位置应该放谁。1所在的数组红色箭头也可以考虑下一个元素,此时在归并过程中1这个元素就有序了,接下来比较2和4,2更小把2放到最终数组中,蓝色的箭头考虑下一个位置应该放谁,2所在的数组红色箭头可以移动一个位置,接下来比较3和4的大小,3小放到最终数组中,蓝色的箭头考虑下一个位置应该放谁,3所在的数组红色箭头可以向后移动一个位置,上面归并过程中1 2 3 已经排好序了,考察4和6这两个元素,4小放到最终数组中,蓝色的箭头考虑下一个位置应该放谁,4所在的数组红色箭头可以向后移动一个位置,接下来考虑5和6 依次类推,本质就是两个已经排好序的数组,来比较当前头部元素谁更小就放到最终数组中。(使用递归实现自顶向下的归并排序)
将下面两个数组中指引当前要考虑元素的位置索引叫 i,j,上面最终数组中的索引位置叫k i j 指向的是当前正在考虑的元素,k表示的是这两个元素比较后应该放到最终归并数组中的位置,k不表示归并结束后放置的最后一个元素的位置,而表示下一个需要放的位置,在程序中我们要维护i,j,k相应的定义,维持变量在算法运行过程中永远满足定义,是写出正确算法的基础,为了能跟踪i,j,k越界情况,我们要定义最左边的元素叫l(left)最右边的元素叫r(right),数组在前闭后闭的空间中 m(middle)放到了第一个排好序数组的最后一个位置 。
代码实现
#include
//将arr[l……mid]和[mid+1……r]两部分进行归并
void __merge(int arr[],int l,int mid,int r)
{
//因为是闭区间所以要+1
int aux[r-l+1],p;
//aux这个空间是从0开始的,arr从l开始的 之间右l的偏移量
// 所以要aux[i-l] = arr[i];
for(p=l;p<=r;p++)
{//将当前要处理的arr所有元素都 复制到aux数组中
aux[p-l] = arr[p];
} //完成临时空间
//i j 分别指向两个子数组开头的位置
int i=l,j=mid+1,k;//从l-r使用k进行遍历
for(k=l;k<=r;k++)
{
//i超出了范围 i>mid k还没遍历完 说明j索引所指向的子数组中的元素
//还没有归并回去 此时应该取j所指数组中的元素
if(i>mid)
{
arr[k]=aux[j-l];
j++;
}
else if(j>r)
{
arr[k]=aux[i-l];
i++;
}
//i指向数组中的元素小
else if(aux[i-l]=r)
{
return ;
}
int mid= l+(r-l)/2;
__mergeSort(arr,l,mid);
__mergeSort(arr,mid+1,r);
//对于近乎有序的加上 if(arr[mid]>arr[mid+1])
if(arr[mid]>arr[mid+1])
{
__merge(arr,l,mid,r);
}
}
void mergeSort(int arr[],int n)
{
__mergeSort(arr,0,n-1);
} 迭代方式实现归并排序
自底向上的归并排序
#include
#define min(a,b) amid k还没遍历完 说明j索引所指向的子数组中的元素
//还没有归并回去 此时应该取j所指数组中的元素
if(i>mid)
{
arr[k]=aux[j-l];
j++;
}
else if(j>r)
{
arr[k]=aux[i-l];
i++;
}
//i指向数组中的元素小
else if(aux[i-l]n-1时取n-1
}
}
}
int main()
{
int a[10]={5,9,8,6,2,1,4,61,88,74};
int len = sizeof(a)/sizeof(a[0]);
mergeSortBU(a,len);
int i;
for(i=0;i 可以进行优化 1.当数据小于一定规模时选择插入排序2.当arr[mid]>arr[mid+1]时在进行__merge(arr,l,mid,r);
快速排序
思路:每次从当前考虑的数组中选择一个元素作为基点,比如说在这个数组中选择4,把4移到排好序时该在的位置,使得整个数组有一个性质4之前的元素都是小于4的4之后的都是大于4的,对小于4的字数组和大于4的字数组分别用快速排序的思想来排序主逐渐递归下去完成排序。对于快速排序来说最重要的就是如何把选定的元素4移动到正确的位置上,这个过程就是核心。
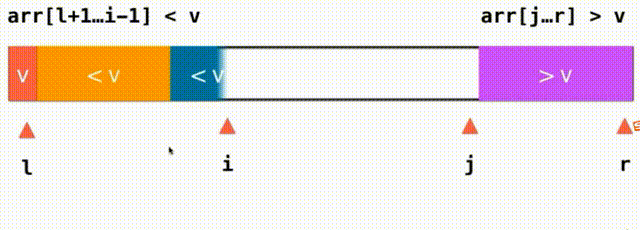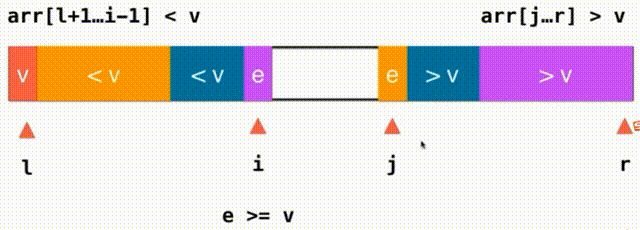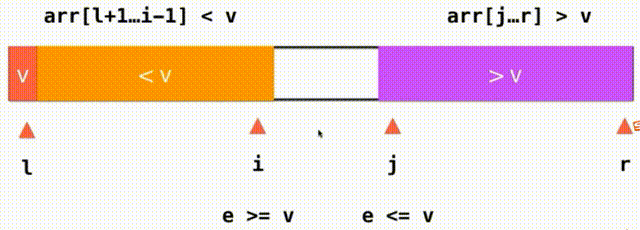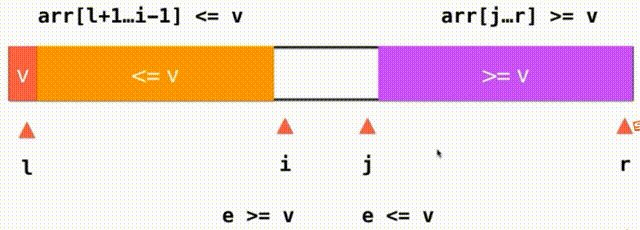
把这个过程叫做partition 使用整个数组的第一个元素来作为分界的标志点,对于这个数组的第一个位置叫做l之后逐渐遍历右边所有没有被访问的元素,在遍历的过程中我们将逐渐的整理让整个数组一部分是小于v这个元素的一部分是大于v这个元素的,在过程中我们要记录那个是大于v和小于v的分界点用j来标记当前访问的元素叫i,这样arr[l+1...j] 思路:之前,我们将小于V大于V的都放在数组的一头,i逐渐从左到右遍历完整个数组。现在,我们将小于V大于V的放在数组的两端,我们需要一个j索引来记录大于V要扫描的下一个元素的位置,我们从i这个位置开始向后扫描,当我们面对的元素是小于v的就继续向后扫描,直到碰到元素e>=v停止,对于j也是这样,我们从j向前扫描,如果大于V继续向前看直到碰到元素e<=v停止,i和j交换一下位置就行了,此时,橙色的都是小于V的元素,紫色的都是大于V的的元素i向后查看元素,j向前查看元素,直到i和j重合遍历数组完毕。左面是<=v右面是>=v,把=v的元素分成了左右两部分,如果i和j指向的都是等于V的元素,两个元素还要交换一下位置,这样就不会存在大量元素都集中在橙色或紫色的情况,也因此能把有大量重复的值的时候平分开来 对于使用快速排序的思想给大量带有重复值的数组排序还有一种经典的方式叫叫做三路快排(Quick Sort 3Ways) 思路:把数组分成小于V等于V大于V三部分,这样分割后在递归过程中等于V的部分就不用管了只需要递归对小于V大于V部分进行同样的快速排序就好了。lt(less than)索引指向小于V部分最后一个元素arr[l+1...lt] #include快速排序优化
#include #include