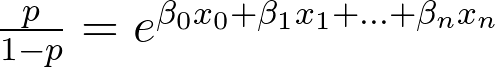黑盒模型实际上比逻辑回归更具可解释性
作者:Samuele Mazzanti
编译:ronghuaiyang
正文共:3701 字 17 图
预计阅读时间:11 分钟
导读
如何让复杂的模型具备可解释性,SHAP值是一个很好的工具,但是SHAP值不是很好理解,如果能将SHAP值转化为对概率的影响,看起来就很舒服了。
在可解释性和高性能之间的永恒的争斗
从事数据科学工作的人更了解这一点:关于机器学习的一个老生常谈是,你必须在以下两者之间做出选择:
简单、可靠和可解释的算法,如逻辑回归
强大的算法,达到更高的精度,但代价是失去任何可理解的清晰度,如梯度提升或支持向量机
这些模型通常被称为“黑盒子”,这意味着你知道输入什么,输出什么,但却没有办法理解引擎盖下到底发生了什么。
在接下来的文章中,我们将会证明,不仅不需要在能力和可解释性之间进行选择,而且强大的模型甚至比那些较浅的模型更容易解释。
数据
作为说明,我们将使用最著名的数据集之一:标志性的泰坦尼克号数据集。我们有很多关于泰坦尼克号乘客的变量,我们想要预测每位乘客幸存的可能性有多大。
我们可以使用的变量有:
Pclass:客舱等级
Sex:乘客性别
Age:乘客年龄
SibSp:泰坦尼克号上的兄弟姐妹/配偶人数
Parch:泰坦尼克上的家长/儿童人数
Fare:乘客票价
Embarked:登船口岸
(注:为简单起见,删除了一些其他变量,几乎没有进行数据预处理)。
数据是这样的:
前5位乘客的数据逻辑回归
对于涉及到的分类问题,通常采用逻辑回归作为基线。
在对定的特征(客舱等级、乘客性别和登船口岸)进行了one-hot编码后,我们对训练数据进行了简单的逻辑回归。在验证集上计算的精度为81.56%。
我们能从这个模型中得到什么启示?由于Logistic回归的构建是这样的:
分析围绕β。很容易看到的增加1个单位的xⱼ,几率将增加exp(βⱼ)。
对此的解释很简单:年龄每增加1岁,几率就会增加0.961倍。
那就是:
A, 25岁:生存几率 = 3
B,除了年龄(26岁)外的所有变量和A相同:生存几率= 3×0.961 = 2.883
这个模型在可解释性方面的局限性是不言而喻的:
exp(βⱼ)和几率之间的关系是线性的,也就是说,2岁和12岁之间的差别和52岁和62岁是一样的。
没有任何的信息交互,例如,不管乘客是在头等舱还是三等舱,60岁对幸存概率的影响是一样的。
试试黑盒子:Catboost和SHAP
现在让我们尝试一个“黑箱”模型。在本例中,我们将使用Catboost,这是一种在决策树上进行梯度提升的算法。在相同的训练数据上执行一个快速的Catboost(没有任何超参数的调优)(这次不需要独热编码),结果是验证数据的87.15%准确性。
正如我们所预期的,Catboost的性能显著优于逻辑回归 (87.15% vs. 81.56%)。到目前为止,这不足为奇。
现在,机器学习中一个价值6.4万美元的问题是:如果Catboost在预测未知数据方面比逻辑回归做得更好,那么我们是否应该相信它?
这得视情况而定。如果这是一个Kaggle竞赛,答案可能“是”,但一般来说“肯定不是!”。如果你想知道为什么,看看这些事件,亚马逊“性别歧视的AI招聘工具“,或微软“种族主义聊天机器人”。
因此,为了弄清楚Catboost正在做什么决策,另一个名为SHAP(SHapley Additive exPlanations)的工具来帮助我们。SHAP(可能是机器学习可解释性的最先进技术)诞生于2017年,它是对任何预测算法的输出进行反向工程的绝妙方式。
将SHAP分析应用到我们的数据中,Catboost输出将生成一个矩阵,该矩阵与原始数据矩阵具有相同的维数,包含SHAP值。SHAP值看起来是这样的:
前5个乘客的SHAP值SHAP值越高,生还概率越高,反之亦然。此外,大于0的SHAP值会导致概率的增加,小于0的值会导致概率的减少。
每个SHAP值表示,这是这里的重要部分,个体所观察到的变量水平对个体最终预测概率的边际效应。
这意味着:假设对于第一个个体,我们知道除了年龄以外的所有变量。它的SHAP和是-0.36 -0.76 +0.05 -0.03 -0.3 -0.08 = -1,48。一旦我们知道了个体的年龄(也考虑了年龄和其他变量之间的相互作用),我们就可以更新总和:-1.48 +0.11 =-1.37。
SHAP: 大象在房间里
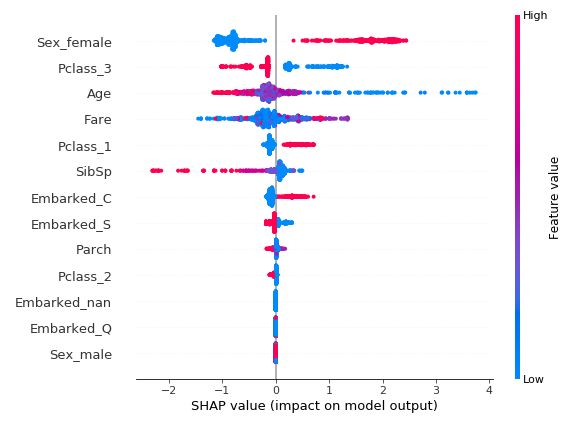
你可以使用Python的SHAP库来进行绘图(包含了基本的关于SHAP值的描述性统计)。例如,你可以很容易地获得一个图表,该图表汇总了每个观察的SHAP值,并按特征进行细分。我们的例子:
我们能看见房间里的大象吗?
如果你把这个情节展示给门外汉(甚至是你的老板),他可能会说:“颜色很漂亮,但是下面的刻度是什么?是美元吗?公斤吗?年吗?“
简而言之,SHAP值对于人类来说是不可理解的(即使对于数据科学家来说也是如此)。
从SHAP值到预测概率
概率的概念要容易理解得多。
从SHAP到预测概率想要从SHAP过渡到概率,最明显的方法是绘制相对于SHAP和(每个个体)的预测的生存概率(每个个体)。
很明显,这是一个确定性函数。也就是说,我们可以毫无差错地从一个量转换到另一个量。毕竟,两者之间的唯一区别是,概率必然在[0,1],而SHAP可以是任何实数。因此:
其中f(.)是一个单调递增的s型函数,它将任意实数映射到[0,1]区间(为简单起见,f()可以是一个以[0,1]为界的普通插值函数)。
让我们以一个个体为例。假设已知除年龄外的所有变量,其SHAP和为0。现在假设年龄的SHAP值是2。
我们只要知道f()函数就可以量化年龄对预测的生存概率的影响:它就是f(2)-f(0)。在我们的例子中,f(2)-f(0) = 80%-36% = 44%
毫无疑问,生存的概率比SHAP值更容易被理解。
然后怎么办?
根据我们刚刚看到的,从上面看到的SHAP矩阵出发,应用以下公式就足够了:
![]()
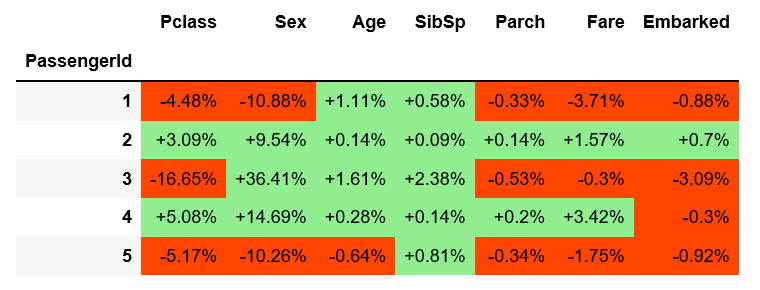
得到下面的:
例如,拥有一张三等舱的票会降低第一个乘客的生存概率-4.48%(相当于-0.36 SHAP)。请注意,3号乘客和5号乘客也在三等舱。由于与其他特征的相互作用,它们对概率的影响(分别为-16.65%和-5.17%)是不同的。
可以对这个矩阵进行几次分析。作为一个例子,我画了一个图。
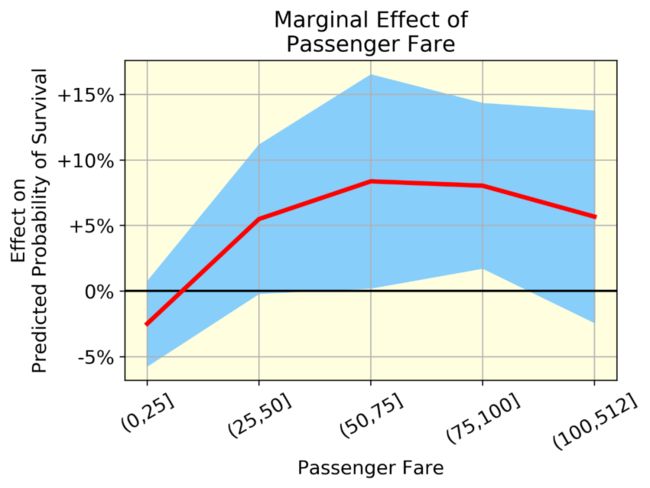
乘客年龄的边际效应乘客票价的边际效应
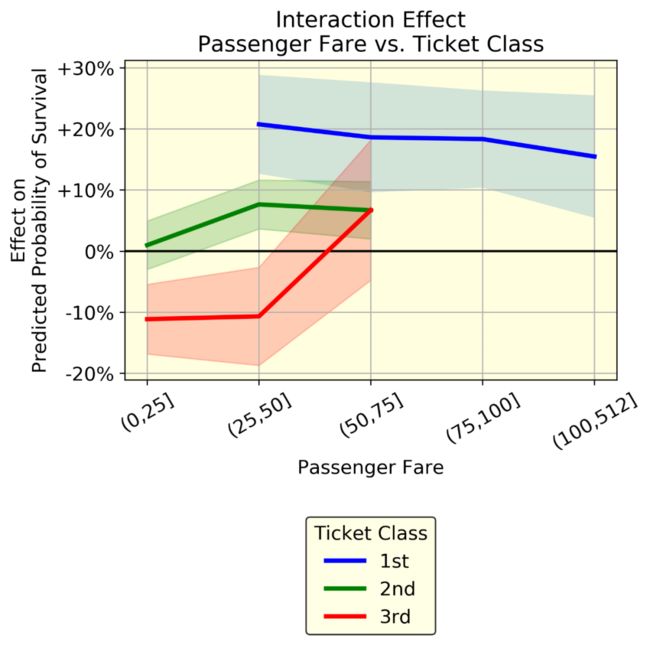
交互作用:乘客票价 vs. 客舱等级
红线表示平均效应(一组中所有个体的年龄效应的均值),蓝带(均值±标准差)表示同一组中个体年龄效应的变异性。变异是由于年龄和其他变量之间的相互作用。
这个方法的可提供的价值:
我们可以用概率来量化效果,而不是用SHAP值。例如,我们可以说,平均来说,60-70岁的人比0-10岁的人(从+14%到-13%)的存活率下降了27%
我们可以可视化非线性效应。例如,看看乘客票价,生存的可能性上升到一个点,然后略有下降
我们可以表示相互作用。例如,乘客票价与客舱等级。如果这两个变量之间没有相互作用,这三条线就是平行的。相反,他们表现出不同的行为。蓝线(头等舱乘客)的票价稍低。特别有趣的是红线(三等舱乘客)的趋势:在两个相同的人乘坐三等舱时,支付50 - 75英镑的人比支付50英镑的人更有可能生存下来(从-10%到+5%)。
整理一下
像逻辑回归这样的简单模型做了大量的简化。黑盒模型更灵活,因此更适合复杂(但非常直观)的现实世界行为,如非线性关系和变量之间的交互。
可解释性是指基于人类对现实的感知(包括复杂的行为),以一种人类可理解的方式表达模型的选择。
我们展示了一种将SHAP值转换为概率的方法。这使我们有可能对一个黑匣子进行可视化,并确保它与我们对世界的认识是一致的(在质量和数量上):一个比简单模型所描述的世界更丰富的世界。
快给我代码!
https://github.com/smazzanti/tds_black_box_models_more_explainable/blob/master/Shap2Probas.ipynb
![]()
—END—
英文原文:https://towardsdatascience.com/black-box-models-are-actually-more-explainable-than-a-logistic-regression-f263c22795d
喜欢的话,请给我个好看吧!![]()