Java数据结构与算法解析(十七)——斜堆
斜堆概述
斜堆(Skew heap)也叫自适应堆(self-adjusting heap),它是左斜堆的一个变种。和左倾堆一样,它通常也用于实现优先队列;作为一种自适应的左斜堆,它的合并操作的时间复杂度也是O(lg n)。
它与左斜堆的差别是:
(1) 斜堆的节点没有”零距离”这个属性,而左斜堆则有。
(2) 斜堆的合并操作和左倾堆的合并操作算法不同。

斜堆的合并操作
(1) 如果一个空斜堆与一个非空斜堆合并,返回非空斜堆。
(2) 如果两个斜堆都非空,那么比较两个根节点,取较小堆的根节点为新的根节点。将”较小堆的根节点的右孩子”和”较大堆”进行合并。
(3) 合并后,交换新堆根节点的左孩子和右孩子。
第(3)步是斜堆和左倾堆的合并操作差别的关键所在,如果是左倾堆,则合并后要比较左右孩子的零距离大小,若右孩子的零距离 > 左孩子的零距离,则交换左右孩子;最后,在设置根的零距离。
由于合并都是沿著最右路径进行的,经过合并之后,新斜堆的最右路径长度必然增加,这会影响下一次合并的效率。所以合并后,通过交换左右子树,使整棵树的最右路径长度非常小(这是启发规则)。然而斜堆不记录节点的距离,在操作时,从下往上,沿著合并的路径,在每个节点处都交换左右子树。通过不断交换左右子树,斜堆把最右路径甩向左边了。
递归实现合并
1.比较两个堆; 设p是具有更小的root的键值的堆,q是另一个堆,r是合併后的结果堆。
2.令r的root是p(具有最小root键值),r的右子树为p的左子树。
3.令r的左子树为p的右子树与q合併的结果。
非递归合并实现
1.把每个堆的每棵(递归意义下)最右子树切下来。这使得得到的每棵树的右子树均为空。
2.按root的键值的升序排列这些树。
3.迭代合併具有最大root键值的两棵树:
1)具有次大root键值的树的右子树必定为空。把其左子树与右子树
2)交换。现在该树的左子树为空。
具有最大root键值的树作为具有次大root键值树的左子树。

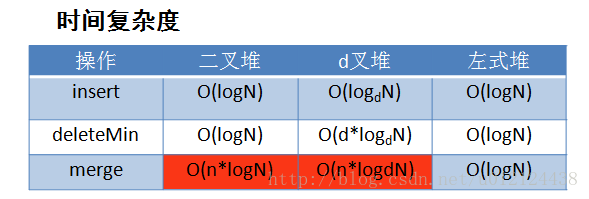
性能比较
斜堆的代码实现
1. 基本定义
public class SkewHeap<T extends Comparable<T>> {
private SkewNode mRoot; // 根结点
private class SkewNode<T extends Comparable<T>> {
T key; // 关键字(键值)
SkewNode left; // 左孩子
SkewNode right; // 右孩子
public SkewNode(T key, SkewNode left, SkewNode right) {
this.key = key;
this.left = left;
this.right = right;
}
public String toString() {
return "key:"+key;
}
}
} SkewNode是斜堆对应的节点类。
SkewHeap是斜堆类,它包含了斜堆的根节点,以及斜堆的操作。
2. 合并
/*
* 合并"斜堆x"和"斜堆y"
*/
private SkewNode merge(SkewNode x, SkewNode y) {
if(x == null) return y;
if(y == null) return x;
// 合并x和y时,将x作为合并后的树的根;
// 这里的操作是保证: x的key < y的key
if(x.key.compareTo(y.key) > 0) {
SkewNode tmp = x;
x = y;
y = tmp;
}
// 将x的右孩子和y合并,
// 合并后直接交换x的左右孩子,而不需要像左倾堆一样考虑它们的npl。
SkewNode tmp = merge(x.right, y);
x.right = x.left;
x.left = tmp;
return x;
}
public void merge(SkewHeap other) {
this.mRoot = merge(this.mRoot, other.mRoot);
} merge(x, y)是内部接口,作用是合并x和y这两个斜堆,并返回得到的新堆的根节点。
merge(other)是外部接口,作用是将other合并到当前堆中。
3. 添加
/*
* 新建结点(key),并将其插入到斜堆中
*
* 参数说明:
* key 插入结点的键值
*/
public void insert(T key) {
SkewNode node = new SkewNode(key,null,null);
// 如果新建结点失败,则返回。
if (node != null)
this.mRoot = merge(this.mRoot, node);
} insert(key)的作用是新建键值为key的节点,并将其加入到当前斜堆中。
4. 删除
/*
* 删除根结点
*
* 返回值:
* 返回被删除的节点的键值
*/
public T remove() {
if (this.mRoot == null)
return null;
T key = this.mRoot.key;
SkewNode l = this.mRoot.left;
SkewNode r = this.mRoot.right;
this.mRoot = null; // 删除根节点
this.mRoot = merge(l, r); // 合并左右子树
return key;
} remove()的作用是删除斜堆的最小节点。
完整代码
public class SkewHeap> {
private SkewNode mRoot; // 根结点
private class SkewNode> {
T key; // 关键字(键值)
SkewNode left; // 左孩子
SkewNode right; // 右孩子
public SkewNode(T key, SkewNode left, SkewNode right) {
this.key = key;
this.left = left;
this.right = right;
}
public String toString() {
return "key:"+key;
}
}
public SkewHeap() {
mRoot = null;
}
/*
* 前序遍历"斜堆"
*/
private void preOrder(SkewNode heap) {
if(heap != null) {
System.out.print(heap.key+" ");
preOrder(heap.left);
preOrder(heap.right);
}
}
public void preOrder() {
preOrder(mRoot);
}
/*
* 中序遍历"斜堆"
*/
private void inOrder(SkewNode heap) {
if(heap != null) {
inOrder(heap.left);
System.out.print(heap.key+" ");
inOrder(heap.right);
}
}
public void inOrder() {
inOrder(mRoot);
}
/*
* 后序遍历"斜堆"
*/
private void postOrder(SkewNode heap) {
if(heap != null)
{
postOrder(heap.left);
postOrder(heap.right);
System.out.print(heap.key+" ");
}
}
public void postOrder() {
postOrder(mRoot);
}
/*
* 合并"斜堆x"和"斜堆y"
*/
private SkewNode merge(SkewNode x, SkewNode y) {
if(x == null) return y;
if(y == null) return x;
// 合并x和y时,将x作为合并后的树的根;
// 这里的操作是保证: x的key < y的key
if(x.key.compareTo(y.key) > 0) {
SkewNode tmp = x;
x = y;
y = tmp;
}
// 将x的右孩子和y合并,
// 合并后直接交换x的左右孩子,而不需要像左倾堆一样考虑它们的npl。
SkewNode tmp = merge(x.right, y);
x.right = x.left;
x.left = tmp;
return x;
}
public void merge(SkewHeap other) {
this.mRoot = merge(this.mRoot, other.mRoot);
}
/*
* 新建结点(key),并将其插入到斜堆中
*
* 参数说明:
* key 插入结点的键值
*/
public void insert(T key) {
SkewNode node = new SkewNode(key,null,null);
// 如果新建结点失败,则返回。
if (node != null)
this.mRoot = merge(this.mRoot, node);
}
/*
* 删除根结点
*
* 返回值:
* 返回被删除的节点的键值
*/
public T remove() {
if (this.mRoot == null)
return null;
T key = this.mRoot.key;
SkewNode l = this.mRoot.left;
SkewNode r = this.mRoot.right;
this.mRoot = null; // 删除根节点
this.mRoot = merge(l, r); // 合并左右子树
return key;
}
/*
* 销毁斜堆
*/
private void destroy(SkewNode heap) {
if (heap==null)
return ;
if (heap.left != null)
destroy(heap.left);
if (heap.right != null)
destroy(heap.right);
heap=null;
}
public void clear() {
destroy(mRoot);
mRoot = null;
}
/*
* 打印"斜堆"
*
* key -- 节点的键值
* direction -- 0,表示该节点是根节点;
* -1,表示该节点是它的父结点的左孩子;
* 1,表示该节点是它的父结点的右孩子。
*/
private void print(SkewNode heap, T key, int direction) {
if(heap != null) {
if(direction==0) // heap是根节点
System.out.printf("%2d is root\n", heap.key);
else // heap是分支节点
System.out.printf("%2d is %2d's %6s child\n", heap.key, key, direction==1?"right" : "left");
print(heap.left, heap.key, -1);
print(heap.right,heap.key, 1);
}
}
public void print() {
if (mRoot != null)
print(mRoot, mRoot.key, 0);
}
} 测试代码
public class SkewHeapTest {
public static void main(String[] args) {
int a[]= {10,40,24,30,36,20,12,16};
int b[]= {17,13,11,15,19,21,23};
SkewHeap ha=new SkewHeap();
SkewHeap hb=new SkewHeap();
System.out.printf("== 斜堆(ha)中依次添加: ");
for(int i=0; iout.printf("%d ", a[i]);
ha.insert(a[i]);
}
System.out.printf("\n== 斜堆(ha)的详细信息: \n");
ha.print();
System.out.printf("\n== 斜堆(hb)中依次添加: ");
for(int i=0; iout.printf("%d ", b[i]);
hb.insert(b[i]);
}
System.out.printf("\n== 斜堆(hb)的详细信息: \n");
hb.print();
// 将"斜堆hb"合并到"斜堆ha"中。
ha.merge(hb);
System.out.printf("\n== 合并ha和hb后的详细信息: \n");
ha.print();
}
}