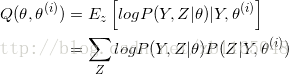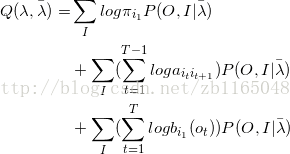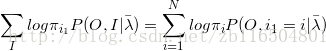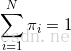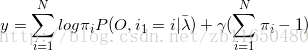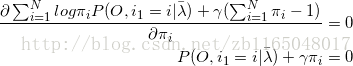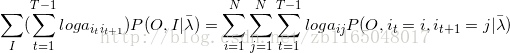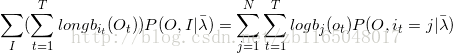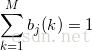HMM——前向后向算法

1. 前言

解决HMM的第二个问题：学习问题， 已知观测序列，需要估计模型参数，使得在该模型下观测序列 P(观测序列 | 模型参数)最大，用的是极大似然估计方法估计参数。

根据已知观测序列和对应的状态序列，或者说只有观测序列，将学习过程分为监督和无监督学习方法

主要参考《李航统计学习》、《PRML》

2. 监督学习方法

给定了s个长度相同的观测序列和对应的状态序列（相当于有s个样本，所有样本长度一样）

然后我们需要做的就是统计三种频率：

① 在样本中，从t 时刻的各状态转移到 t+1时刻的各状态的频率，比如第一个状态转移到第二个状态共有3次，第2个状态转移到第三个状态共有10次，等。。。。。

据此能够推导出状态转移概率

② 在样本中，每对（某个状态j，某个观测k）出现的频率，就是状态为j 观测为k的概率，即混淆矩阵

③在样本中，统计s个样本中初始状态为 的频率就是初始状态概率πi

缺点就是：监督学习需要人工标注训练数据，代价高

3.前向-后向算法

3.1 目标

其它称呼有：Baum-Welch算法

主要针对只有观测序列没有对应的状态序列的情况

这一部分在《统计学习方法》中推导的非常好，主要利用的是拉格朗日乘子法求解

已知：训练数据是S个长度为T的观测序列,没有对应的状态序列

求解：学习隐马尔科夫的参数，包括：转移矩阵、混淆矩阵、初始概率

思路：

因为HMM中引入了隐状态，所以设隐状态序列为I，那么HMM就可以当做一个具有隐变量的概率模型：

其实这个式子就有点像一种边缘概率:

只不过将这个概率加了一个条件，是在HMM的模型参数下计算的，就变成了条件概率。

求解的时候利用E-M算法求解即可（EM中，E代表expectation，是求期望；M代表的是maximization，求极大；合起来EM算法就被称为期望值最大化算法）

3.2 EM步骤简述

摘自《统计学习方法》

输入：观测变量数据Y，隐变量数据Z，联合分布 P(Y, Z | θ)，条件分布 P( Z | Y , θ)

输出：模型参数 θ

步骤：

① 选择参数初值，开始迭代

② E步：记为第 i 次迭代参数θ的估计值，在第 i+1 次迭代E步，计算

第二个等式的第二项是给定观测数据Y和当前的估计参数下隐变量数据Z的条件概率分布

③ M步：求使得极大化的θ，确定第 i+1 次迭代的参数的估计值

④ 重复第②和③步，直到收敛

3.3求解HMM模型参数

(1) 确定完全数据的对数似然函数

观测数据：

隐藏数据：

完全数据：

完全数据的对数似然函数就是

②EM算法之E：求Q函数

式子中是HMM模型参数的当前估计值，λ 是要极大化的HMM模型参数

对于前面一半，根据概率有向图的联合概率分布，我们知道

两式相乘就可以得到：

根据P(O,I | λ)可以将 Q 函数可以改写为：

式中的求和是对所有训练数据的序列长度T进行的

③ EM算法之M：极大化Q函数求解模型参数π、A、B

观察E步骤的式子发现三个参数刚好分别在三项中，所以单独对每一项求解就行了

第一步先求π:

注意，π只与初始状态有关，第一项可以写成

意思就是在模型参数已知的条件下，初始时候的各种状态以及对应的初始观测的概率的和

限制条件就是对于某种观测，初始的所有状态，其概率和为1，例如，第一天观测为晴天时候，海藻的干燥、湿润、潮湿三个状态概率和为1

那么就可以根据拉格朗日乘法计算了,设

那么令其偏导数等于零

对 i 求和得到

再带回偏导为0的式子中得到

第二步求转移矩阵A

将第二项改写为

找到约束条件为

意思就是上一个隐状态到当前所有隐状态的转移概率和为1，比如今天是晴天，那么到明天得隐状态转移：晴天->多云，晴天->雨天，晴天->晴天的概率和为1

依旧根据拉格朗日乘子法得到

第三步求混淆矩阵

将第三项改写为

找到约束条件为

也就是说一个隐状态对应的所有观测概率和为1，比如天气为晴天的时候，对应的海藻干燥、湿润、潮湿的概率和为1

但是有一个需要注意的是只有当观测状态为当前所求导的状态时候，对的偏导数才不为0，其实也就相当于的时候才是偏导不为0,书中用表示，最终偏导以后求得：

3.4 Baum-Welch算法

该求得都求了，那么具体的HMM模型参数估计算法就是：

输入：观测数据

输出：HMM的模型参数

(1) 初始化：

对n=0，选取得到模型

(2) 递推，对n=1,2,...

分别计算上面的三个偏导

(3) 计算到最后一次迭代就得到最终结果了

后续分析一下HMM的代码再另行添加