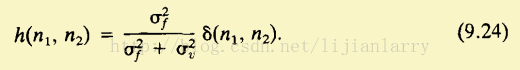基于积分图的维纳滤波算法

先了解一下维纳滤波原理：

维纳滤波（wiener filtering) 一种基于最小均方误差准则、对平稳过程的最优估计器。这种滤波器的输出与期望输出之间的均方误差为最小，因此，它是一个最佳滤波系统。它可用于提取被平稳噪声所污染的信号。
从连续的（或离散的）输入数据中滤除噪声和干扰以提取有用信息的过程称为滤波，这是信号处理中经常采用的主要方法之一，具有十分重要的应用价值，而相应的装置称为滤波器。根据滤波器的输出是否为输入的线性函数，可将它分为线性滤波器和非线性滤波器两种。维纳滤波器是一种线性滤波器。

--《百度百科》

下面我们来看看名著“Two-dimensional signal and image processing”里面的解释：

（书籍太贵，上千一本，只好看英文版，水平有限，请各位专家斧正）：

9.2.4 自适应维纳滤波

图9.9 是大多数去除加性噪声的自适应图像复原算法流程：

根据噪声图像和先验知识，我们能够使用一些基于滤波图像的局部细节方法。其中一个方法就是局部方差。随空间变化的滤波器h(n1,n2)是由图像局部信息和附加先验知识决定的函数。

空变滤波器应用在噪声图像的局部区域。噪声是宽频带的（从低频到高配较为均匀的噪声），空变滤波器是低通的。如强度均匀的区域，图像的细节分量比主分量包含了更多的噪声信息，因此，在去除这种噪声领域，应用了一大批低通滤波器。但是，由于细节分量包含了小信号变化，大批的低通滤波器没有显著的效果。在图像的的主分量上，如边缘表达了主信号分量，仅有少部分低通滤波器在不影响原信号的前提下有些效果。这样做不会去除很多噪声信息，而且相同的噪声在主分量里面较细节分量是不明显的。

基于局部图像信息的特殊的方法改进了算法，空变滤波器h(n1,n2)是由图像局部信息和可获得的先验知识决定的函数。在9.2.1节讨论了一种自适应的维纳滤波器。

由图9.3所示，维纳滤波器需要整幅图像的信号均值mf，噪声均值mv，信号功率谱Pf(w1，w2)和噪声功率谱Pv(w1，w2)，这些信息可以局部估算。这种方法已在一种空变维纳滤波中实现。即使在这种方法里，许多变量还是不确定的，这依赖于mf，mv，Pf(w1，w2)和Pv(w1，w2)的局部估算和空变维纳滤波器的应用效果。我们会改进一种特殊的算法来说明这种方法。

我们首先假设加性噪声v(n1，n2)是零均值和白化且方差为（随机变量的协方差为0，不相关）。他的功率谱Pv(w1,w2)：

在小的局部区域中，信号f(n1,n2)被认为是稳定的。在局部区域里，信号f(n1,n2)为：

mf是f(n1,n2)的均值，是标准差。w(n1,n2)是具有单位方差的零均值白噪声。式（9.22）是一个对于一些有代表性的图像来说的经验模型。见（Trussell and Hunt;Kuan et al.  (1985)）

在式（9.22）中，信号f(n1,n2)是由空变局部均值mf和空变局部方差的白噪声构成的。在局部区域里，维纳滤波器H(w1,w2)：

从式（9.23）中看出，空变滤波器h(n1,n2)是成比例的脉冲响应，

结合图9.3和式（9.24），处理后的图像p(n1,n2)，在局部区域可以表示成：

如果，我们假设mf和在每个像素都是不同的;

公式（9.26）就是算法的核心（见Lee（1980））

说明一下式（9.26）各个变量的含义：

g(n1,n2）是待处理的图像（含噪声的图像）

mf(n1,n2)是图像局部均值（假设局部大小为9*9，类似均值滤波，就是卷积核的大小）

其他变量上面已经讨论，无需赘述！

公式中变量的计算，相信大家都很熟悉了。

只有两点：

1）需要计算的是每个像素所在的图像局部区域（假设9*9）的均值和方差。本文是使用积分图方法加速算法运行，参考我的博文 “基于积分图的均值滤波算法”。

2）噪声的方差约等于图像方差的均值

图像大小：1080P（1920*1080）

滤波器卷积核：9*9

算法耗时：

matlab：2.08秒

本文所用算法 debug版：0.1704秒；release版：0.0537秒

CPU型号：Intel(R) Core(TM) i5-2400 CPU @ 3.10Hz

效果图：