转载声明:http://blog.csdn.net/alpc_neverfarewell/article/details/39160735
题意:
zzy开了一家公司,然后他为公司制定了人事制度:为每个员工都定一个直接的上属(除了zzy自己),这样就把公司表示成了一个树形的人事关系图,树的最顶端就是zzy自己。如果a的直接上属是b则称a是b的一级下属,接下去的依次称为2级、3级……k级下属。
由于如zzy奇葩的想法,他将改变一部分员工的工资,方法依旧是将员工原来的工资异或一个数,得到新的工资。
(这是中文题意,不可能看不懂吧)
个人感想:
这道题目很有意思,就是有一个又有趣的思想,用线段树维护bfs序,然后通过最近公共祖先(LCA),加上二分就可以找到当前 老板 的c级员工的范围.
这道题还给了个重要的思想,就是区间异或和,这我也没接触过,一道题补了好多知识点,维护bfs序这个我是从来没想到过的,确实不会,
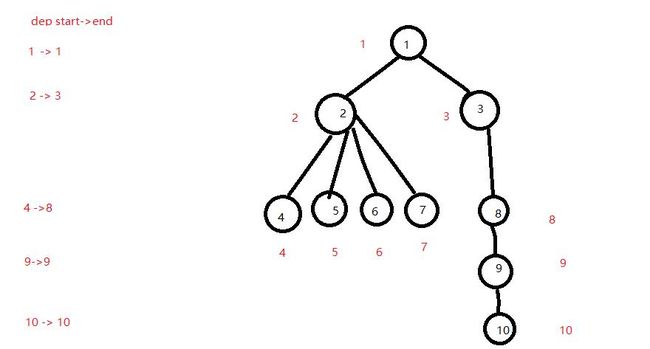
首先先做一遍bfs
我们就可以知道每个深度的区间范围
知道这个有有什么用?我们可以对深度范围进行二分,找到对应的父节点的c级员工节点范围并用线段树更新
例如 现在我要找2的 1级员工
我们知道 depth[2]+1==3
第3层的范围是 4-8.
那么我们就二分这个区间点,并且往上走c级
我们就要找到一个 parent[x][c]2 最左节点, 和parent[y][c]>2的左的y,然后y-1 就是2的最右节点了, 然后就可以用线段树维护
我觉得有点神奇,…只是我对这个理解不深啊,
其实我就看了一会转载的博客我就懂了…
我出的最大问题不在建树,只是二分,
因为有可能所查询的节点 根本没c级员工,那只是别人的位置有而已
那么我怎么二分出来 并且 判断这个区间(x,y)合法?
我一直习惯用(r-l>1) 进行二分,这样做有点难度就是 可能你2个点刚好相差1,所有两个位置都没检测,那还要特殊处理,那就好麻烦了…
所以啊,还是我修行不够啊…
挺好的一道题目,值得深思.
分析:线段树+二分+最近公共祖先
AC代码:
/* Author:GavinjouElephant
* Title:
* Number:
* main meanning:
*
*
*
*/
#include
using namespace std;
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
