线段树与树状数组学习总结——线段树

线段树

什么是线段树

先说一下什么是线段树吧
大家都知道，初中课本中对于线的定义：

点动成线

那么就是说一条线段可以分成若干个点，再想想我们最常用的一维数组，构成数组的是一个个的变量，如果把变量看成一个个点，那么数组就是一条线了！
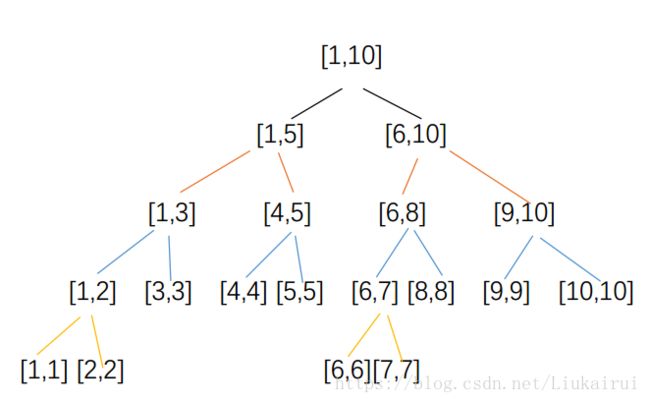
而线段树，就是一棵由线段构成的二叉树，每个结点都代表一条线段 [a,b]（也就是我们前面说的一串变量）。非叶子的结点所对应的线段都有两个子结点，左儿子代表的线段为 [a,(a+b)/2]，右儿子代表的线段为 [((a+b)/2)+1,b]。使用线段树这一数据结构，可以查找一个连续区间中节点的信息，也可以修改一个连续区间中结点的信息。
那么为什么不用普通的数组而是把数组上又加了”坨”树呢？

想想我们当是为什么要学习链表这个数据结构，因为数组对于元素的添加与删除效率太低！而线段树也是为了解决这个问题的所以线段树的作用是：

优化区间操作的复杂度。

如图这就是一个线段树（建议自己根据定义自己画一下）

线段树的单点更新

这一小节我们先看单点更新
顾名思义，单点更新就是只更新一个叶子节点啦
线段树这一部分函数的参数比较多注意区分！
我们先看两个基础的操作

1.修改

就是将数据改了呗，可以使加减或者是覆盖，这个的话，具体实现的时候稍微改一下即可！
上代码(时间复杂度:O(logN)可以从这里看出其高效性)

void up(int p){
    s[p]=s[p*2]+s[p*2+1];
}

void modify(int p,int l,int r,int x,int v){
    if(l==r){
        s[p]+=v;
        return;
    }    
    int mid=(l+r)/2;
    if(x<=mid){
        modify(p*2,l,mid,x,v);
    }else {
        modify(p*2+1,mid+1,r,x,v);    
    }
    up(p);
}

说明：
1.网上有两种代码，一种没有up…但是大多数人的都有，于是我就用了有up的了。
2.up函数作用：把儿子结点的信息更新到父亲结点
3.molify函数：这个就是修改函数啦，说一下变量
–1.p：表示当前位置的节点编号，例如我们在一开始是要在全局进行修改，于是就把p定为根节点。随着修改的进行，我们要修改p来到达其他节点，例如从a节点到a的右孩子就是：p=P*2+1，就像我们平时用的cur一样。
–2.l和r:l和r表示的是当前锁定的区间的范围，例如刚开始l=1，r=n，就是说范围在[1,n]上(也就是全局)，但是我发现目标在根的左孩子上，那么我就要更改l,r为l=l,r=(l+r)/2了。
–3.x:就是要更改的节点编号
–4.v:要更改的值

注意：一定要自己走一遍！！！

2.查询：

就是查询区间内节点的值

int query(int p,int l,int r,int x,int y){
    if(x<=l&&r<=y){
        return s[p];
    }
    int mid=(l+r)/2,res=0;
    if(x<=mid){
        res+=query(p*2,l,mid,x,y);
    }
    if(y>mid){
        res+=query(p*2+1,mid+1,r,x,y);
    }
    return res;
}

说明：
–1.p和上面一样
–2.l,r和上面一样是当前锁定的节点范围，一定要注意！！！！
–3.x,y是我要查询的区间，这个在就是调用函数的时候说明的区间，不变！！！，注意区别与l，r的关系！！！

3.建树

为什么最后说这个？
因为我学的时候这就不是一个模块
只需要注意建的树s[]的数组必须开四倍空间！！！

至此所有的单点更新内容全部结束！
给出模板代码：

#include 
using namespace std;
const int MAX_N=10010;
int s[4*MAX_N];

void up(int p){
    s[p]=s[p*2]+s[p*2+1];
}

void modify(int p,int l,int r,int x,int v){
    if(l==r){
        s[p]+=v;
        return;
    }    
    int mid=(l+r)/2;
    if(x<=mid){
        modify(p*2,l,mid,x,v);
    }else {
        modify(p*2+1,mid+1,r,x,v);    
    }
    up(p);
}

int query(int p,int l,int r,int x,int y){
    if(x<=l&&r<=y){
        return s[p];
    }
    int mid=(l+r)/2,res=0;
    if(x<=mid){
        res+=query(p*2,l,mid,x,y);
    }
    if(y>mid){
        res+=query(p*2+1,mid+1,r,x,y);
    }
    return res;
}

int main() {
    int n;
    cin>>n;
    for(int i=1;i<=n;i++){
        int d;
        cin>>d;
        modify(1,1,n,i,d);
    }
    int q;
    cin>>q;
    while(q--){
        int d,x,y;
        cin>>d>>x>>y;
        if(d==0){
            modify(1,1,n,x,y);
        }else{
            cout<1,1,n,x,y)<return 0;
}

---

线段树的区间更新

还是顾名思义，线段树的区间更新就是把段的数据统一更新了。
当然我们可以反复执行单点更新的molify实现，但是效率呢？
线段树的特点就是牺牲空间换时间，例如：
我要反复执行[1,1000]区间赋值为1，再赋值为2，再赋值为1，再赋值为2…往复循环，那还不如memset高效呢！
所以我们不能像单点更新一样言听计从了，有时候也要皮一下，于是我们有了lazy标记，什么意思呢，你让我把[1,1000]更新为1，我说好的，然后打一个标记到[1,1000]的子树的根节点上写上改为1000，但是我没有把根节点的子节点的数据改了，除非你来访问了，你访问多少，我打多少，你不访问，程序结束的时候我可能都没去真正的赋值！
同样类似的标记命名还有col等，以下代码为col的。这里直接上模板代码了，函数名与单点的一样，参数略有不同，自己想。

#include 
using namespace std;
const int MAX_N=10010;
int s[4*MAX_N],col[4*MAX_N];

void up(int p){
    s[p]=s[p*2]+s[p*2+1];
}

void down(int p,int l,int r){
    if(col[p]){
        int mid=(l+r)/2;
        s[p*2]+=col[p]*(mid-l+1);
        s[p*2+1]+=col[p]*(r-mid);
        col[p*2]+=col[p];
        col[p*2+1]+=col[p];
        col[p]=0;
    }
}

void modify(int p, int l, int r, int x, int y, int c) {
    if (x <= l && r <= y) {
        s[p] += (r - l + 1) * c;
        col[p] += c;
        return;
    }
    down(p, l, r);
    int mid = (l + r) / 2;
    if (x <= mid) {
        modify(p * 2, l, mid, x, y, c);
    }
    if (y > mid) {
        modify(p * 2 + 1, mid + 1, r, x, y, c);
    }
    up(p);
}

int query(int p, int l, int r, int x, int y) {
    if (x <= l && r <= y) {
        return s[p];
    }
    down(p, l, r);
    int mid = (l + r) / 2, res = 0;
    if (x <= mid) {
        res += query(p * 2, l, mid, x, y);
    }
    if (y > mid) {
        res += query(p * 2 + 1, mid + 1, r, x, y);
    }
    return res;
}

int main() {
    int n;
    cin>>n;
    for (int i = 1; i <= n; ++i) {
    int d;
    cin >> d;
    modify(1, 1, n, i, i, d);
    }
    int q;
    cin>>q;
    while (q--) {
    int d, x, y, c;
    cin >> d >> x >> y;
    if (d == 0) {
        cin >> c;
        modify(1, 1, n, x, y, c);
    } else {
        cout << query(1, 1, n, x, y) << endl;
        }   
    }
    return 0;
}