Pruning Convolutional Neural Networks For Resource Efficient Inference

论文地址：https://arxiv.org/abs/1611.06440v2

英伟达出品的模型剪枝论文，NVIDIA Transfer Learning Toolkit就是基于这篇论文进行实现的？

0 摘要

我们提出了一种新的对神经网络中卷积核进行剪枝的算法以实现高效推理。我们将基于贪婪标准的修剪与通过反向传播的微调交错 - 实现了一种高效的的过程，在修剪后的网络中保持了良好的泛化能力。我们提出了一种基于泰勒展开的新的评价标准，该标准近似于修剪网络参数引起的代价函数的变化。我们专注于转移学习，其中大型预训练网络适用于专门任务。与其他标准(例如，使用卷积核或特征映射的范数对用于细粒度分类的大型CNN进行修剪只取决于梯度的一阶信息)相比，本文提出的标准表现出了优越的性能。我们还表明，剪枝在理论上可以导致适应性3D卷积滤波器的大小减少超过10倍，并且在递归手势分类器中精度略有下降。最后，我们展示了将我们的方法应用于大型ImageNet数据集的结果，以强调我们方法的灵活性。

1 简介

卷积神经网络（CNN）广泛用于计算机视觉应用，包括目标分类和定位、行人和汽车检测以及视频分类。像这样的许多问题都集中在专门的领域，只有少量精心收集的训练数据。在这些情况下，可以通过微调先前在更大的标记视觉数据集上训练的现有深度网络来提高准确度，例如来自ImageNet的图像（Russakovsky等，2015）或来自Sports-1M的视频（Karpathy等。，2014）。虽然这种形式的迁移学习获取了最先进的精确度，但由于微调网络的重量级架构所需的时间、功率和内存，因此推理是比较耗时的。

虽然现代深度CNN由多种层类型组成，但预测期间的运行时间主要由卷积层的计算量决定。为了加快推理速度，我们修剪整个特征图，以便即使在嵌入式设备上也可以高效运行生成的网络。我们将基于贪婪标准的修剪与通过反向传播进行微调交错，这是一种高效的计算过程，可以在修剪后的网络中保持良好的泛化。

神经网络剪枝是神经网络早期发展的先驱（Reed，1993）。Optimal Brain Damage（LeCun等，1990）和Optimal Brain Surgeon（Hassibi＆Stork，1993）利用二阶泰勒展开来选择要删除的参数，使用剪枝作为正则化来改进训练和泛化过程。该方法需要部分或完全地计算Hessian矩阵，这增加了标准微调的存储和计算成本。

与我们的工作一致，Anwar等人(2015)描述了在特征映射和内核级别的卷积层中的结构化修剪，以及在内核中规则性修剪的跨度稀疏性。通过粒子滤波完成剪枝，其中配置通过误分类率加权。该方法在小型CNN上显示出良好的结果，但是不适合于更大的CNN。

Han等人(2015)通过使用强大的 l2 正则化项进行微调并丢弃低于预定义阈值的参数来实现更简单的剪枝方法。这种非结构化修剪对于网络压缩非常有效，并且该方法展示了用于核内剪枝的良好性能。但压缩可能无法直接转化为更快的推理，因为现代硬件李艳计算中的规律性实现高吞吐量。因此，可能需要专门的硬件来实现具有核内稀疏性的网络（Han et al。，2016）的高效推理。这种方法还需要比较长的微调时间，这可能超过原始网络训练时间的3倍或更多。Wen等，2016; Zhou等，2016; Alvarez＆Salzmann，2016; Lebedev＆Lempitsky，2016提出了基于稀疏性的网络参数正则化来惩罚不重要的参数。基于正则化的剪枝技术需要对每层进行灵敏度分析，这增加了额外的计算。相反，我们的方法依赖于对所有层的标准进行全局重新缩放，并且不需要灵敏度估计。此外，我们的方法更快，因为我们直接修剪不重要的参数，而不是通过正规化下的优化使它们的值足够小。

其他方法，包括将参数与相关权重相结合（Srinivas＆Babu，2015），降低精度（Gupta等，2015; Rastegari等，2016）或张量分解（Kim等，2015）。这些方法通常需要单独的训练过程或重要的微调，可能可以与我们的方法相结合以获得额外的加速。

2 方法

本文提出的剪枝方法包括以下步骤：

• 微调网络直到目标任务收敛;
• 剪枝和进一步微调的反复迭代;
• 在达到准确性和修剪目标之间的权衡后停止剪枝，例如浮点运算（FLOP）或内存利用率。

实现过程很简单，但其成功取决于设置了正确的剪枝标准。在本节中，我们将介绍几种有效的剪枝标准和相关的技术注意事项。

假设训练集$D=\{\{X=x_0,x_1,\cdots ,x_N\},y=\{y_0,y_1,\cdots ,y_N\}\}$，X和y分别表示输入和输出。网络参数$W=\{(w_1^1,b_1^1),(w_1^2,b_1^2),\cdots ,(w_L^{C_l},b_L^{C_l})\}$优化以最小化损失值$C(D|W)$。最常用的损失函数是负对数似然函数。代价函数的选择与剪枝无关，仅取决于原始网络要解决的任务。在迁移学习的情况下，我们使用在相关但不同的数据集上预先训练的参数W0来预先初始化大型网络。

在剪枝过程中，我们改进了一个参数子集，即便保持了网络的准确性，$C(D|W^{{}^{\prime }})\approx C(D|W)$。这对应于组合优化：
$$mi{n}_{w^{{}^{\prime }}}|C(D|W^{{}^{\prime }})-C(D|W)|,s.t.||W^{{}^{\prime }}|{|}_0\le B$$

$||W^{{}^{\prime }}|{|}_0\le B$表示$W^{{}^{\prime }}$中非零参数的数量小于B。直观地，如果W0 = W，我们达到误差函数的全局最小值，但是$||W^{{}^{\prime }}|{|}_0$也将具有其最大$l_0$范数值。

找到一个好的参数子集，同时保持尽可能接近原始的损失值是一个组合问题。它将需要对所选数据子集的成本函数进行$2^{|W|}$次评估。对于当前网络，计算量太大难以计算：例如，VGG-16具有|W| = 4224个卷积特征映射。虽然对于任何合理大小的网络都不可能完全解决这种优化问题，但在本文中我们研究了一类贪婪的方法。

从完整参数W开始，我们迭代地识别并移除最不重要的参数，如图1所示。通过在每次迭代时删除参数，我们确保最终满足$W^{{}^{\prime }}$的$l_0$约束。

由于我们将分析重点放在修剪卷积层的特征图上，我们用$z_l\in R^{H_l\times W_l\times C_l}$表示图像集得特征映射，其大小为$H_l\times W_l$，具有$C_l$个通道。该特征映射可以是网络的输入$z_0$，也可以是网络的卷积层的输出$z_l,l\in [1,2,\cdots ,L]$。单个特征图表示成$z_l^{(k)},k\in [1,2,\cdots ,C_l]$。具有参数$w_l^{(k)}\in R^{C_{l-1}\times p\times p}$的卷积层$l$对输入的特征映射$z_{l-1}$应用卷积运算:
$$z_l^{(k)}=g_l^{(k)}R(z_{l-1}\ast w_l^{(k)}+b_l^{(k)})$$
其中，$z_l^{(k)}\in R^{H_l\times W_l}$是每一个大小为$p\times p$的卷积核和其输入特征映射卷积结果和偏差$b_l^{(k)}$相加的结果。这里引入了一个剪枝门函数$g_l\in \{0,1{\}}^{C_l}$，用于决定某特定特征映射应该在前向过程中保留还是被剪掉。g也被向量化，安装$W^{{}^{\prime }}=gW$进行使用。

2.1 oracle剪枝

最小化完整模型和修剪模型之间的准确度差异取决于在每个步骤中识别称为显著性的“最不重要”参数的标准。最佳标准是对每个参数的精确经验评估，我们表示为oracle标准，通过依次消除每个非零参数$w\in W^{{}^{\prime }}$并记录代价差异来实现。

我们区分了使用这个oracle估计重要性的两种方法：

• Oracle-loss量化代价函数的改变量$C(D|W^{{}^{\prime }})-C(D|W)$
• oracle-abs量化代价函数改变的绝对值$|C(D|W^{{}^{\prime }})-C(D|W)|$

虽然两者都不鼓励修剪增加损失，但是oracle-loss版本鼓励通过修剪可以减少损失，而oracle-abs不考虑损失的改变方向，只是惩罚任何修剪造成的损失变化。

虽然oracle对于这个贪婪程序是最佳的，但计算成本过高，需要在训练数据集上对$||W^{{}^{\prime }}|{|}_0$进行评估，对每个剩余的非零参数进行一次评估。由于参数重要性的估计是这种修剪方法的准确性和效率的关键，因此我们在性能和估算成本方面提出并评估了若干标准。

2.2 剪枝标准

有许多启发式标准比oracle计算效率更高。对于评估特征映射的重要性（以及隐式计算它的卷积核的集合）的具体情况，合理的标准包括：

• 核权重的$l_2$范数；
• 特征映射激活值的均值、标准差和比例；
• 激活值和预测值之间的互信息。

我们在以下段落中描述这些标准，并提出基于泰勒展开的新标准。

最小化权重：按内核权重的大小进行修剪可能是最简单的标准，并且在微调过程中不需要任何额外的计算。在根据一组权重的范数进行修剪的情况下，将该标准评估设置为：${\Theta }_{MW}:R^{C_{l-1}\times p\times p}\to R$，${\Theta }_{MW}(w)=\frac{1}{|w|}{\sum }_i{w}_i^2$，$w$表示权重集向量化后的维度。应用这种修剪的动机是，具有低$l2$范数的卷积核检测到的特征不如具有高范数的卷积核检测到的特征重要。这可以通过应用l1或l2正则化来辅助训练，这将推动不重要的内核具有更小的值。

激活值：ReLU激活普及的原因之一是诱导了激活的稀疏性，允许卷积层充当特征检测器。因此，可以合理地假设如果激活值（输出特征图）很小，则该特征检测器对于手头的预测任务并不重要。我们可以通过平均激活来评估，对于激活值$a=z_l^{(k)}$，${\Theta }_{MA}:R^{H_l\times W_l\times C_l}\to R$，${\Theta }_{MA}(a)=\frac{1}{|a|}{\sum }_i{a}_i$，或者可以通过激活值的标准差进行评估，${\Theta }_{M{A}_{s}td}(a)=\sqrt{\frac{1}{|a|}{\sum }_i(a_i-u_a{)}^2}$。

互信息：互信息(MI)衡量一个变量中有关另一个变量的信息量。我们将MI作为修剪的标准，${\Theta }_{MI}:R^{H_l\times W_l\times C_l}\to R$，${\Theta }_{MI}(a)=MI(a,y)$，y是神经网络的输出。MI适用于连续变量。为了简化计算，我们使用信息增益(Information Gain,IG)替换它，IG针对量化变量定义为$IG(y|x)=H(x)+H(y)-H(x,y)$，H(x)表示变量x的熵。我们累积了许多更新的激活和真值的统计数据，然后量化并计算IG。

泰勒展开：我们将修剪作为优化问题，试图找到$W^{{}^{\prime }}$，具有有限的非零元素，即最小化$|△C(h_i)|=|C(D|W^{{}^{\prime }})-C(D|W)|$。通过基于泰勒展开的这种方法，我们直接通过去除特定参数来近似损失函数的变化。使用$h_i$表示参数 i 的输出，针对特征映射，$h=\{z_0^{(1)},z_0^{(2)},\cdots ,z_L^{(C_l)}\}$。为了方便起见，我们认为损失函数同样取决于参数和从参数计算的输出：$C(D|h_i)=C(D|(w,b{)}_i)$。假设独立于参数，我们有：
$$|△C(h_i)|=|C(D|h_i=0)-C(D,h_i)|$$
其中，如果$h_i$被修剪掉，则$C(D,h_i=0)$表示该参数为0时的损失值；如果$h_i$没有被修剪掉，则$C(D,h_i)$表示具有该参数时的损失。虽然参数实际上是相互依赖的，但我们已经在训练期间的每个梯度步骤中做出了独立性假设。

为了近似$△C(h_i)$，我们使用一阶泰勒展开。对于函数$f(x)$，函数在x=a处的泰勒展开为：
$$f(x)=\sum _{p=0}^P\frac{f^{(p)}(a)}{p!}(x-a{)}^p+R_p(x)$$
其中，$f^{(p)}(a)$为 f 在点 a 处的 p 阶导数。$R_p(x)$为 p 阶剩余项。在$h_i=0$处使用一阶泰勒展开近似$C(D,h_i=0)$可得：
$$C(D,h_i=0)=C(D,h_i)-\frac{\delta C}{\delta h_i}{h}_i+R_1(h_i=0)$$

$R_1(h_i=0)$可以通过拉格朗日形式计算：
$$R_1(h_i=0)=\frac{{\delta }^{2}C}{\delta (h_i^2=ϵ)}\frac{h_i^2}{2}$$
$ϵ$是介于0到$h_i$之间的实数。这里我们忽略一阶剩余项，主要是由于需要进行大量计算，但部分原因是广泛使用的ReLU激活函数鼓励较小的二阶项。

最后，忽略掉剩余项，将式子带入可得：
$${\Theta }_{TE}(h_i)=|△C(h_i)|=|C(D,h_i)-\frac{\delta C}{\delta h_i}{h}_i-C(D,h_i)|=|\frac{\delta C}{\delta h_i}{h}_i|$$

直观地，该标准修剪那些代价函数对特征映射$h_i$具有几乎平坦梯度的参数。这种方法需要累积激活值的乘积和代价函数对激活值的梯度，这可以很容易地从反向传播中计算出来。${\Theta }_{TE}$针对多变量输出，例如对特征映射，有：

M为特征映射向量化之后得长度。对于minibatch大于1得样本，该标准对minibatch中的每一个样本进行计算并使用T做平均。

独立于我们的工作，Figurnov等人（2016）提出了基于泰勒展开的类似度量，称为impact，以评估空间核在卷积层中的重要性。它表明可以应用相同的度量来评估不同参数组的重要性。

和Optimal Brain Demage之间的关系：上面提出的泰勒标准依赖于近似去除一个特征映射导致的损失变化。核心思想与Optimal Brain Demage（OBD）相同（LeCun等，1990）。在这里，我们更仔细地考虑差异。

主要区别在于泰勒展开的一阶项的处理，在我们的实现中，对于代价函数C和隐藏层激活h，$y=\frac{\partial C}{\partial h}h$。在经过足够的训练之后，梯度项$\frac{\partial C}{\partial h}\to 0$，E(y) = 0。此时y提供的信息很少，因此OBD将该项视为零，并侧重于二阶项。

然而，y的方差不为零，并且与局部函数激活h的稳定性相关。通过考虑修剪引起的代价的绝对变化（如公式3所示），我们使用一阶项|y|的绝对值。基于样本独立同分布的假设，$E(|y|)=\sigma \sqrt{2}/\sqrt{\pi }$，其中$\sigma$是y的标准差，为半正态分布的期望值。所以，当y趋向于0，|y|的期望正比于y的方差，y的方差作为修剪标准经验上看具备更多的信息。

作为额外的好处，我们避免计算二阶泰勒展开项，或其简化 - Hessian的对角线，如OBD所要求的。

我们发现将提出的泰勒标准与OBD进行比较非常重要。如原始论文（LeCun等，1990; 1998）中所述，OBD可以与标准反向传播算法类似地高效实现，当与标准微调一起使用时，后向传播时间和存储占用会加倍。原始OBD算法的高效实现可能需要基于像Theano这样的自动微分框架进行重大更改，以有效地仅计算Hessian的对角线而不是完整矩阵。一些研究人员试图用近似技术解决这个问题（Martens，2010; Martens等，2012）。在我们的实现中，我们高效计算Hessian矢量积（Pearlmutter，1994）和由（Bekas等人，2007）提出的矩阵对角近似，请参考附录中的更多细节。在当前实现中，OBD比用于显著性估计的Taylor技术慢30倍，并且对于迭代修剪慢3倍，但是如原始论文中提到的那样，不同的实现只能慢50％。

OBD近似于带符号的损失，作者的方法近似于损失的绝对损失。作者发现使用绝对损失进行修剪可以取得更好的准确率。

Average Percentage of Zeros(APoZ)：胡等人（2016）提出使用激活的稀疏性进行网络修剪。ReLU激活函数在推理期间施加稀疏性，并且输出中正的激活值的比例可以确定神经元的重要性。直观地说，这是一个很好的标准，但是无论网络的目标是什么，第一层的特征图都有类似的APoZ，因为他们学会像Gabor一样滤波器。我们将使用APoZ来估计特征图的显著性。

2.3 归一化

某些标准返回“原始”值，其比例随网络中参数层的深度而变化。一个简单的逐层“l2 标准化”可以实现跨层的重新缩放：

2.4 FLOPS正则化修剪

应用修剪的主要原因之一是减少网络中的操作数量。由于输入特征映射和卷积核的数量和大小不同，来自不同层的特征映射需要不同的计算量。考虑到这一点，我们引入FLOP正则化：

其中，$\lambda$控制正则化的数量。作者使用的是$\lambda =10^{-3}$。${\Theta }^{flop}$的计算基于卷积使用滑动窗方式进行实现的假设。可以应用其他正则化条件，例如，存储大小、内核大小或内存占用量。

为了计算浮点运算（FLOP）的数量，我们假设卷积是作为滑动窗口实现的，非线性函数是免费计算的。对于卷积内核，我们有：
$$FLOPS=2HW(C_{in}{K}^2+1)C_{out}$$
其中，H、W、$C_{in}$是输入特征图的高、宽和通道数。 K是正方形卷积核的大小，$C_{out}$是输出通道数。

对于全连接层，其FLOP为 (2I - 1)O，其中I表示输入维度，O表示输出维度。

3 结果

我们根据实验研究了上一节中详述的修剪标准和程序，以解决各种问题。我们将许多实验集中在迁移学习问题上，这是很适合于修剪的应用环境。我们还提出了修剪大型网络原始任务的结果，以便与现有的修剪文献进行更直接的比较。实验在Theano（Theano Development Team，2016）内进行。除非另有说明，否则针对每个问题对相应的训练集执行训练和修剪，同时在适当的留出集上报告结果。对于所有实验，我们在每次修剪迭代时修剪单个特征图，允许对标准进行微调和重新评估以考虑参数之间的依赖性。

3.1 使用oracle修剪的结果

我们首先明确地计算oracle规则用于视觉迁移学习问题时的单个修剪迭代。我们使用Caltech-UCSD Birds 200-2011数据集（Wah et al。，2011）对VGG-16网络（Simonyan＆Zisserman，2014）进行微调，以对鸟类进行分类。该数据集由近6000个训练图像和5700个测试图像组成，覆盖200种鸟类。我们使用学习率为0.0001的VGG-16微调60个时期，使用未剪切的图像实现72.2％的测试精度。

为了计算oracle，我们评估了从微调的VGG-16网络中删除每个单独的特征映射所导致的损失变化。（有关其他分析，请参阅附录A.3。）我们根据对损失的贡献对特征图进行排名，其中等级1表示最重要的特征图 - 删除它导致损失的最大增加 - 而等级4224表示最不重要的特征图。全局等级的统计显示在图2中，由卷积层分组。我们观察到：（1）中位数的全局重要性趋于随着深度而减小。（2）具有最大池化的层往往比没有使用最大池化的层更重要。（VGG-16在第2,4,7,10和13层之后汇集。）但是，（3）最大和最小等级表明每个层都有一些全局重要的特征映射，也有一些不太重要的特征映射。结合后续实验的结果，我们选择鼓励平衡修剪，在所有层上分配选择。

接下来，我们使用预先计算的oracle排名迭代地修剪网络。在本实验中，我们不会更新网络参数或迭代之间的oracle排名。在许多修剪迭代中，训练精度在图3中示出。令人惊讶的是，通过最小的绝对损失变化（Oracle-abs）进行修剪比通过对损失的净影响（Oracle损失）进行修剪产生了更高的准确性。即使oracle表明单独删除一些特征图可能会减少损失，但由于引起的大的绝对变化，不稳定性会累积。这些结果支持通过代价函数的绝对差进行修剪，如公式1所示。

3.2 对比评估本文提出的标准和oracle标准

为了评估计算效率标准作为oracle的替代，我们计算Spearman的秩相关性，估计两个预测器提供单调相关输出的程度，即使他们的关系不是线性的。给定每个参数 i 的oracle和标准等级$d_i=rank({\Theta }_{oracle}(i))-rank({\Theta }_{criterion}(i))$之间的差异，计算等级相关性：

其中N是参数的数量（和最高等级）。该相关系数取[-1,1]，其中-1表示完全负相关，0表示无相关，1表示完全正相关。

我们在表1中显示Spearman的相关性，将oracle-abs排名与一组网络/数据集上的不同标准的排名进行比较，其中一些将在稍后介绍。在修剪迭代之前或修剪迭代之间的微调期间，根据训练数据计算数据相关标准（除了权重大小之外的所有标准）。作为健全性检查，我们评估随机排名并观察所有层的0.0相关性。“Per layer”分析显示每个卷积层内的排名，而“All layers”描述了跨层的排名。虽然有几个标准在具有原始值的层上不能很好地扩展，但是逐层标准化可以显著提高性能。泰勒标准在所有标准中具有最高的相关性，在层内和跨层（具有L2标准化）。OBD显示未使用标准化时各层之间的最佳相关性;它还显示了ImageNet数据集上相关性的最佳结果。

3.3 对基于Imagenet微调的网络进行剪枝

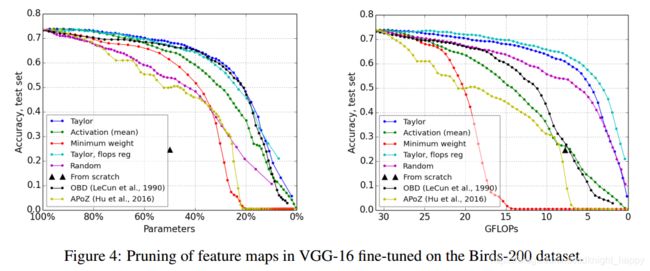
我们现在评估关于两个迁移学习问题的完整迭代修剪过程。我们专注于减少卷积特征映射的数量和总估计浮点运算（FLOP）。对于相对较小的数据集而言，如果不依赖于迁移学习，则难以进行细粒度识别。布兰森等人（2014）表明，在Birds-200数据集上从头开始训练CNN的测试精度仅为10.9％。我们将结果与训练随机初始化的CNN进行比较，每层的参数数量减半，表示为“从头开始”。

图4显示了在Birds-200数据集上进行微调后对VGG-16的修剪（如前所述）。在每次修剪迭代时，我们删除单个特征图，然后执行30个小批量SGD更新，批量大小为32，动量为0.9，学习率为1e-4，权重衰减为1e-4。该图描绘了相对于修剪率（左）和估计的GFLOP（右）的准确度。泰勒标准显示几乎整个修剪比范围的最高精度，并且FLOP正则化表明相对于操作次数的最佳性能。OBD在参数方面表现出稍差的修剪性能，但在FLOP方面却存在显著差异。

在图5中，我们在适应牛津花102数据集（Nilsback＆Zisserman，2008）后，显示了对AlexNet的CaffeNet实施的修剪（Krizhevsky等，2012），2040次训练和来自102种花的6129个测试图像。表1总结了与oracle-abs的标准相关性。我们最初使用0.001的学习速率微调网络20个epoch，最终测试精度达到80.1％。然后修剪程序如之前针对Birds-200所述，除了在修剪迭代之间仅有10个小批量更新。我们观察到Taylor和OBD标准在参数数量和GFLOP方面的优越性能。

我们观察到泰勒标准显示出最佳性能，其中OBD紧随其后具有较低的Spearman等级相关系数。由于Hessian的对角线的计算，实施OBD需要更多的努力，并且它比仅依赖于一阶梯度的Taylor标准慢50％至300％。

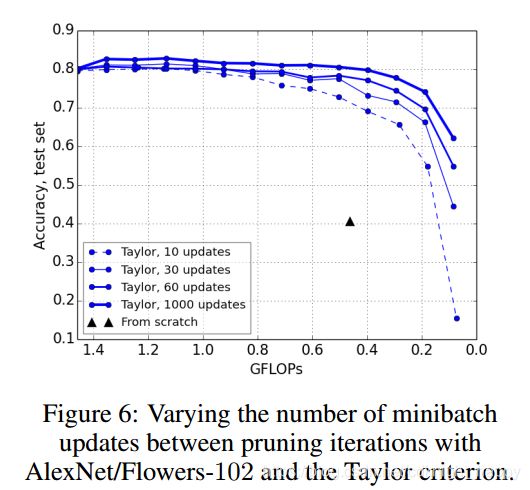
图6显示了使用泰勒技术进行修剪以及修剪迭代之间的不同数量的微调更新。增加更新次数会带来更高的准确性，但代价是修剪过程的额外运行时间。

在修剪期间，我们观察到精确度略有下降。其中一个原因是修剪迭代之间的微调。初始的网络通过更长的微调和更好的优化参数搜索，具有更好的准确性。例如，在额外的128k更新后，Birds-200上的未修剪得VGG16网络的准确率达到75％。在130k更新后，Flowers-102上的AlexNet上升到82.9％。应该注意的是，通过对修剪网络的进一步微调，我们也可以实现更高的精度，因此精度的一对一比较是粗略的。

3.4 修复用于手势识别的循环3D-CNN网络

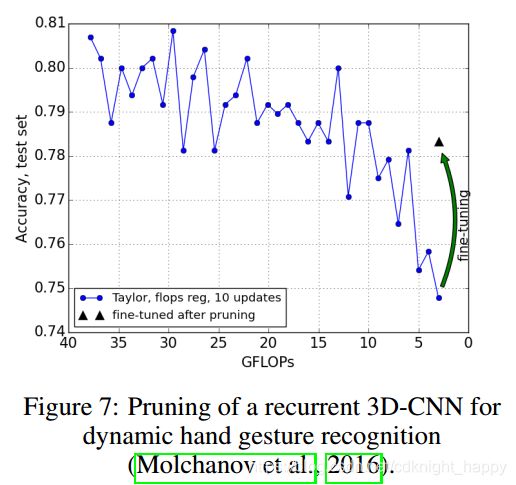
Molchanov等（2016）使用大型递归神经网络的识别视频流中的25个动态手势。通过向Sports-1M视频数据集（Karpathy等人，2014）预训练的3D-CNN添加循环连接并对手势数据集进行微调来构建网络。完整网络在深度模态训练时达到80.7％的准确度，但单个推理需要估计37.8 GFLOP，对于嵌入式GPU上的部署来说计算量太大了。使用具有学习速率0.0003，动量0.9，FLOP正则化10-3的泰勒标准进行几次修剪迭代，我们将推断计算量减少到3.0 GFLOP，如图7所示。虽然修剪造成错误率提升了6%，额外的微调可以恢复大部分丢失的精度，从而产生最终修剪的网络，GFLOP减少12.6倍，精度损失仅为2.5％。

3.5 为ImageNet修剪网络

我们还在大规模ImageNet分类任务上测试我们的修剪方案。在第一个实验中，我们从经过训练的AlexNet的CaffeNet实现开始，该网络具有79.2％的Top-5验证准确度。在修剪迭代之间，我们使用学习率10-4，动量0.9，重量衰减1e-4，批量大小32和50％的dropout进行微调。使用5000个训练图像的子集，我们计算oracle-abs和Spearman与标准的秩相关性，如表1所示。修剪迹线如图8所示。

我们观察到：1）当在修剪迭代之间使用100次更新时，Taylor比随机或最小权重修剪更好。当结果显示时，w.r.t。FLOPs，与随机修剪的差异仅为0％-4％，但是当用修剪的特征图的数量绘制时，差异更高，1％-10％。2）将更新次数从100增加到1000可以显着提高泰勒标准和随机修剪的修剪性能。

对于第二个实验，除了启用FLOP正则化之外，我们使用与之前相同的参数修剪经过训练的VGG-16网络。我们在两点处停止修剪，11.5和8.0 GFLOPs，并在两个模型中微调另外五个epoch，学习率为10-4。修剪后的微调显著改善了结果：网络修剪到11.5 GFLOPs从Top-5准确率从83％提高到了87％，网络修剪到8.0 GFLOP时准确率从77.8％提高到84.5％。

3.6 速度测量

在修剪过程中，我们测量了FLOP计算的减少，这是一种常见的做法（Han et al。，2015; Lavin，2015a; b）。由于从层中移除整个特征映射，FLOP的改进导致网络的推断时间单调减少。然而，推理所消耗的时间依赖于卷积算子的特定实现、并行化算法、硬件、调度、存储器传输速率等。因此，我们测量所选网络的推理时间的改善，以与表2中的未修剪网络相比查看实际加速。我们通过提出的修剪方案观察到显著的加速。

4 结论

我们提出了一种迭代修剪深度卷积神经网络的新方案。我们发现：
1）根据启发式选择标准，通过在这种情况下迭代地移除最不重要的参数 - 特征图，可以成功地修剪CNN;

2）基于泰勒扩展的标准与其他标准相比有显著改进;

3）标准的每层标准化对于获得全局缩放是重要的。