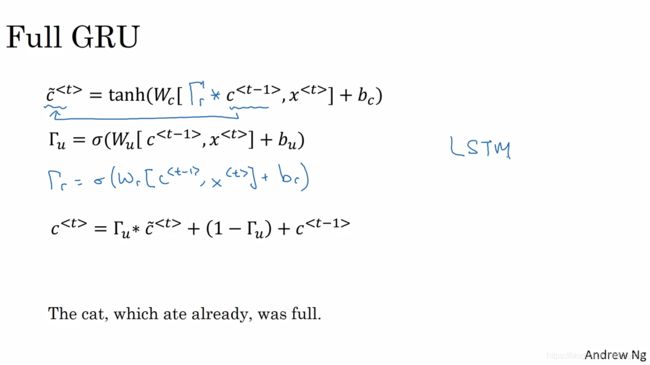Tensorflow tf.keras.layers.GRU
init
__init__(
units,
activation='tanh',
recurrent_activation='sigmoid',
use_bias=True,
kernel_initializer='glorot_uniform',
recurrent_initializer='orthogonal',
bias_initializer='zeros',
kernel_regularizer=None,
recurrent_regularizer=None,
bias_regularizer=None,
activity_regularizer=None,
kernel_constraint=None,
recurrent_constraint=None,
bias_constraint=None,
dropout=0.0,
recurrent_dropout=0.0,
implementation=2,
return_sequences=False,
return_state=False,
go_backwards=False,
stateful=False,
unroll=False,
time_major=False,
reset_after=True,
**kwargs
)
参数
| 参数 | 描述 |
|---|---|
| units | Positive integer, dimensionality of the output space. |
| activation | Activation function to use. Default: hyperbolic tangent (tanh). If you pass None, no activation is applied (ie. “linear” activation: a(x) = x). |
| recurrent_activation | Activation function to use for the recurrent step. Default: sigmoid (sigmoid). If you pass None, no activation is applied (ie. “linear” activation: a(x) = x). |
| use_bias | Boolean, whether the layer uses a bias vector. |
| kernel_initializer | Initializer for the kernel weights matrix, used for the linear transformation of the inputs. |
| recurrent_initializer | Initializer for the recurrent_kernel weights matrix, used for the linear transformation of the recurrent state. |
| bias_initializer | Initializer for the bias vector. |
| kernel_regularizer | Regularizer function applied to the kernel weights matrix. |
| recurrent_regularizer | Regularizer function applied to the recurrent_kernel weights matrix. |
| bias_regularizer | Regularizer function applied to the bias vector. |
| activity_regularizer | Regularizer function applied to the output of the layer (its “activation”)… |
| kernel_constraint | Constraint function applied to the kernel weights matrix. |
| recurrent_constraint | Constraint function applied to the recurrent_kernel weights matrix. |
| bias_constraint | Constraint function applied to the bias vector. |
| dropout | Float between 0 and 1. Fraction of the units to drop for the linear transformation of the inputs. |
| recurrent_dropout | Float between 0 and 1. Fraction of the units to drop for the linear transformation of the recurrent state. |
| implementation | Implementation mode, either 1 or 2. Mode 1 will structure its operations as a larger number of smaller dot products and additions, whereas mode 2 will batch them into fewer, larger operations. These modes will have different performance profiles on different hardware and for different applications. |
| return_sequences | Boolean. Whether to return the last output in the output sequence, or the full sequence. |
| return_state | Boolean. Whether to return the last state in addition to the output. |
| go_backwards | Boolean (default False). If True, process the input sequence backwards and return the reversed sequence. |
| stateful | Boolean (default False). If True, the last state for each sample at index i in a batch will be used as initial state for the sample of index i in the following batch. |
| unroll | Boolean (default False). If True, the network will be unrolled, else a symbolic loop will be used. Unrolling can speed-up a RNN, although it tends to be more memory-intensive. Unrolling is only suitable for short sequences. |
| reset_after | GRU convention (whether to apply reset gate after or before matrix multiplication). False = “before”, True = “after” (default and CuDNN compatible). |
理论
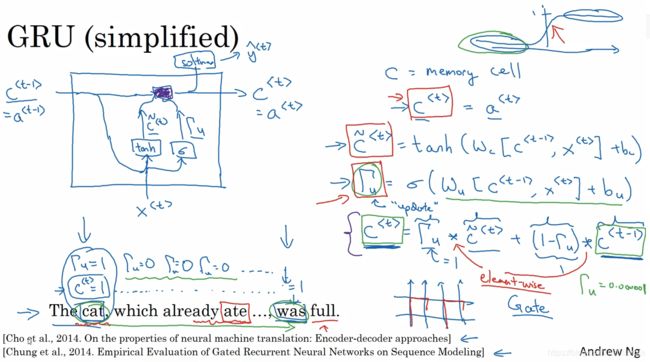
c ^ < t > \hat{c}^{<t>} c^<t>是记忆状态,对应矩阵形状( u n i t s ∗ f e a t u r e s + u n i t s ∗ u n i t s + b i a s units*features+units*units+bias units∗features+units∗units+bias)
Γ u \Gamma_u Γu为更新门(update),式中的δ为sigmoid函数,这让 Γ u \Gamma_u Γu趋向于0或者1。当 Γ u \Gamma_u Γu为0时 c ^ < t > \hat{c}^{<t>} c^<t>= c ^ < t − 1 > \hat{c}^{<t-1>} c^<t−1>,不更新,记忆前一步,反之,更新
Γ u \Gamma_u Γu的矩阵形状是( u n i t s ∗ f e a t u r e s + u n i t s ∗ u n i t s + b i a s units*features+units*units+bias units∗features+units∗units+bias)
Γ r \Gamma_r Γr为记忆门(remember)控制前一时刻的状态被带入到当前状态中的程度, Γ r \Gamma_r Γr为1,带入信息大,重置门用于控制忽略前一时刻状态信息的程度,越小忽略越多
Γ r \Gamma_r Γr的矩阵形状是( u n i t s ∗ f e a t u r e s + u n i t s ∗ u n i t s + b i a s units*features+units*units+bias units∗features+units∗units+bias)
所以GRU层的总参数量为 ( u n i t s ∗ f e a t u r e s + u n i t s ∗ u n i t s + u n i t s ) ∗ 3 (units*features+units*units+units)*3 (units∗features+units∗units+units)∗3
注意:
tensorflow2.0中默认reset_after=True,所以separate biases for input and recurrent kernels因此总参数量为 ( u n i t s ∗ f e a t u r e s + u n i t s ∗ u n i t s + u n i t s + u n i t s ) ∗ 3 (units*features+units*units+units+units)*3 (units∗features+units∗units+units+units)∗3
将input和recurrent kernels的bias分开计算了
参考:
官网
https://www.imooc.com/article/36743
https://stackoverflow.com/questions/57318930/calculating-the-number-of-parameters-of-a-gru-layer-keras