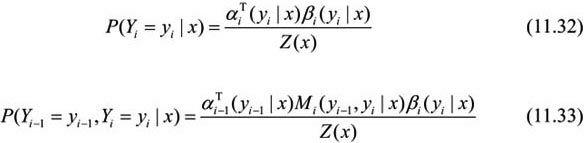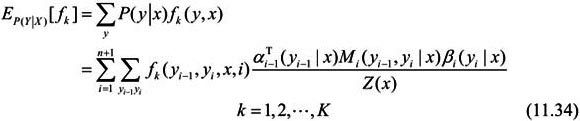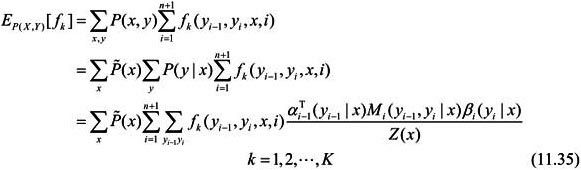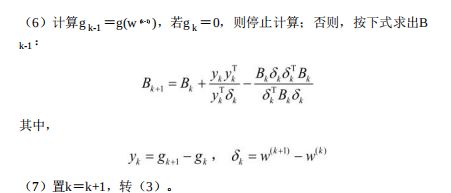统计学习方法---条件随机场
条件随机场的定义
概率无向图模型的联合概率分布P(Y) 可以表示如下:
P ( Y ) = 1 Z ∏ C Ψ C ( Y C ) Z = ∑ Y ∏ C Ψ C ( Y C ) P(Y) = \frac 1 {Z} \prod_C \Psi_C(Y_C) \\ Z = \sum_Y \prod_C\Psi_C(Y_C) P(Y)=Z1C∏ΨC(YC)Z=Y∑C∏ΨC(YC)
因为条件随机场为无向图模型,且势函数通常定义为指数函数,所以其联合概率分布式:
P ( Y ) = 1 Z ∏ C Ψ C ( Y C ) = 1 Z ∏ i = 1 K e x p [ − E i ( Y C i ) ] = 1 Z e x p ∑ i = 1 K [ F i ( Y C i ) ] P(Y) = \frac 1 {Z} \prod_C \Psi_C(Y_C) \\ = \frac 1 Z \prod_{i=1}^K exp[-E_i(Y_{Ci})] \\ = \frac 1 Z exp\sum_{i=1}^K[F_i(Y_{Ci})] P(Y)=Z1C∏ΨC(YC)=Z1i=1∏Kexp[−Ei(YCi)]=Z1expi=1∑K[Fi(YCi)]
这里 K 是指最大团的个数,C是指最大团。
这里的条件随机场为线性链条件随机场,最大团是相邻的两个随机变量。记为 y t − 1 , y t y_{t-1}, y_t yt−1,yt。即可将一个最大团的F函数表示成三个部分。注意,我们这里假设在 y 1 y_1 y1 的前面增加一个在 y 0 y_0 y0 结点
P ( y ∣ x ) = 1 Z e x p ∑ i = 1 T F ( y i − 1 , y i , x , i ) F ( y i − 1 , y t , x ) = Δ y i − 1 , x , i + Δ y i , x , i + Δ y i − 1 , y i , x , i P(y | x) = \frac 1 Z exp\sum_{i=1}^T F(y_{i-1}, y_i, x,i) \\ F(y_{i-1}, y_t, x) = \Delta_{y_{i-1}, x,i} + \Delta_{y_i, x,i} + \Delta_{y_{i-1},y_i, x,i} P(y∣x)=Z1expi=1∑TF(yi−1,yi,x,i)F(yi−1,yt,x)=Δyi−1,x,i+Δyi,x,i+Δyi−1,yi,x,i
Δ y i − 1 , x , i , Δ y i , x , i \Delta_{y_{i-1}, x,i} , \Delta_{y_i, x,i} Δyi−1,x,i,Δyi,x,i 为状态函数,表示的最大团中的点。
Δ y i − 1 , y i , x , i \Delta_{y_{i-1},y_i, x,i} Δyi−1,yi,x,i 为转移函数,表示的最大团中的边。
因为 Δ y i − 1 , x , i \Delta_{y_{i-1}, x,i} Δyi−1,x,i 在上一个最大团的表达式中也存在。所以在这里省略 Δ y i − 1 , x , i \Delta_{y_{i-1}, x,i} Δyi−1,x,i。因此,
F ( y i − 1 , y t , x , i ) = Δ y i , x , i + Δ y i − 1 , y i , x , i F(y_{i-1}, y_t, x,i) = \Delta_{y_i, x,i} + \Delta_{y_{i-1},y_i, x,i} F(yi−1,yt,x,i)=Δyi,x,i+Δyi−1,yi,x,i
令
Δ y i − 1 , y i , x , i = ∑ k = 1 K λ k t k ( y i − 1 , y i , x , i ) Δ y i , x , i = ∑ l = 1 L μ l s l ( y i , x , i ) \Delta_{y_{i-1}, \ y_i, \ x,i} = \sum_{k=1}^K \lambda_k t_k(y_{i-1}, \ y_i, \ x, \ i) \\ \Delta_{y_i, x,i} = \sum_{l = 1}^L \mu_l s_l(y_i, x,i) Δyi−1, yi, x,i=k=1∑Kλktk(yi−1, yi, x, i)Δyi,x,i=l=1∑Lμlsl(yi,x,i)
则,
P ( y ∣ x ) = 1 Z e x p ∑ i = 1 T ( ∑ k = 1 K λ k t k ( y i − 1 , y i , x , i ) + ∑ l = 1 L μ l s l ( y i , x , i ) ) = 1 Z e x p [ ∑ k = 1 K λ k ∑ i = 1 T t k ( y i − 1 , y i , x , i ) + ∑ l = 1 L μ l ∑ i = 1 T s l ( y i , x , i ) ) ] Z = ∑ y e x p ∑ i = 1 T ( ∑ k = 1 K λ k t k ( y i − 1 , y i , x , i ) + ∑ l = 1 L μ l s l ( y i , x , i ) ) P(y | x) = \frac 1 Z exp \sum_{i=1}^T(\sum_{k=1}^K \lambda_k t_k(y_{i-1}, \ y_i, \ x, \ i) + \sum_{l = 1}^L \mu_l s_l(y_i, x,i))\\ = \frac 1 Z exp [\sum_{k=1}^K \lambda_k \sum_{i=1}^T t_k(y_{i-1}, \ y_i, \ x, \ i) + \sum_{l = 1}^L \mu_l \sum_{i=1}^T s_l(y_i, x,i))] \\ Z = \sum_y exp \sum_{i=1}^T(\sum_{k=1}^K \lambda_k t_k(y_{i-1}, \ y_i, \ x, \ i) + \sum_{l = 1}^L \mu_l s_l(y_i, x,i)) P(y∣x)=Z1expi=1∑T(k=1∑Kλktk(yi−1, yi, x, i)+l=1∑Lμlsl(yi,x,i))=Z1exp[k=1∑Kλki=1∑Ttk(yi−1, yi, x, i)+l=1∑Lμli=1∑Tsl(yi,x,i))]Z=y∑expi=1∑T(k=1∑Kλktk(yi−1, yi, x, i)+l=1∑Lμlsl(yi,x,i))
K, L为给定值, t k , s l t_k,s_l tk,sl 是特征函数, λ k , μ l \lambda_k,\mu_l λk,μl是对应的权值。
通常,特征函数 t k , s l t_k,s_l tk,sl 取值为0 或 1;当满足特征条件时取值为1,否则为0。条件随机场全由特征函数和对应的权值确定。
简化形式:
令
y = [ y 1 y 2 ⋯ y T ] , x = [ x 1 x 2 ⋯ x T ] , λ = [ λ 1 λ 2 ⋯ λ K ] , η = [ η 1 η 2 ⋯ η L ] t = [ t 1 t 2 ⋯ t K ] , s = [ s 1 s 2 ⋯ s L ] y = \begin{bmatrix} y_1 \\ y_2 \\ \cdots \\ y_T \end{bmatrix}, x = \begin{bmatrix} x_1 \\ x_2 \\ \cdots \\ x_T \end{bmatrix}, \lambda = \begin{bmatrix} \lambda_1 \\ \lambda_2 \\ \cdots \\ \lambda_K \end{bmatrix}, \eta = \begin{bmatrix} \eta_1 \\ \eta_2 \\ \cdots \\ \eta_L \end{bmatrix} \\ t = \begin{bmatrix} t_1 \\ t_2 \\ \cdots \\ t_K \end{bmatrix} , s = \begin{bmatrix} s_1 \\ s_2 \\ \cdots \\ s_L \end{bmatrix} y=⎣⎢⎢⎡y1y2⋯yT⎦⎥⎥⎤,x=⎣⎢⎢⎡x1x2⋯xT⎦⎥⎥⎤,λ=⎣⎢⎢⎡λ1λ2⋯λK⎦⎥⎥⎤,η=⎣⎢⎢⎡η1η2⋯ηL⎦⎥⎥⎤t=⎣⎢⎢⎡t1t2⋯tK⎦⎥⎥⎤,s=⎣⎢⎢⎡s1s2⋯sL⎦⎥⎥⎤
则简化形式为
P ( y ∣ x ) = 1 Z e x p ( λ T ∑ i = 1 T t ( y i − 1 , y i , x , i ) + μ T ∑ i = 1 T s ( y i , x , i ) Z = ∑ y e x p ( λ T ∑ i = 1 T t ( y i − 1 , y i , x , i ) + μ T ∑ i = 1 T s ( y i , x , i ) P(y|x) = \frac 1 Z exp(\lambda^T \sum_{i=1}^Tt(y_{i-1}, y_i, x, i) + \mu^T \sum_{i=1}^Ts(y_i, x, i) \\ Z = \sum_y exp(\lambda^T \sum_{i=1}^Tt(y_{i-1}, y_i, x, i) + \mu^T \sum_{i=1}^Ts(y_i, x, i) P(y∣x)=Z1exp(λTi=1∑Tt(yi−1,yi,x,i)+μTi=1∑Ts(yi,x,i)Z=y∑exp(λTi=1∑Tt(yi−1,yi,x,i)+μTi=1∑Ts(yi,x,i)
令
W = ( λ η ) K + L F ( y , x ) = ( ∑ i = 1 T t ( y i − 1 , y i , x , i ) ∑ i = 1 T s ( y i , x , i ) ) K + L W = \binom{\lambda}{\eta}_{K+L} \\ \ \\ F(y, x) = \binom{\sum_{i=1}^T t(y_{i-1}, y_i,x,i)}{\sum_{i=1}^T s( y_i,x,i)}_{K+L} W=(ηλ)K+L F(y,x)=(∑i=1Ts(yi,x,i)∑i=1Tt(yi−1,yi,x,i))K+L
则內积的形式:
P ( y ∣ x ) = 1 Z e x p ( w ⋅ F ( y , x ) ) Z = ∑ y e x p ( w ⋅ F ( y , x ) ) P(y|x) = \frac 1 Z \ exp(w \cdot F(y,x)) \\ Z = \sum_yexp(w \cdot F(y,x)) P(y∣x)=Z1 exp(w⋅F(y,x))Z=y∑exp(w⋅F(y,x))
条件随机场的矩阵形式:
条件随机场还可以由矩阵表示。对每个标记序列引进特殊的起点和终点状态标记 y 0 = s t a r t , y T + 1 = s t o p y_0 = start,y_{T+1} = stop y0=start,yT+1=stop
P ( y ∣ x ) = 1 Z e x p [ ∑ i = 1 T ( ∑ k = 1 K λ k t k ( y i − 1 , y i , x , i ) + ∑ l = 1 L μ l s l ( y i , x , i ) ] = 1 Z ∏ i = 1 T + 1 e x p [ ∑ k = 1 K λ k t k ( y i − 1 , y i , x , i ) + ∑ l = 1 L μ l s l ( y i , x , i ) ] P(y | x) = \frac 1 Z exp[ \sum_{i=1}^T(\sum_{k=1}^K \lambda_k t_k(y_{i-1}, \ y_i, \ x, \ i) + \sum_{l = 1}^L \mu_l s_l(y_i, x,i)] \\ = \frac 1 Z \ \prod_{i=1}^{T+1}exp [\sum_{k=1}^K \lambda_k t_k(y_{i-1}, \ y_i, \ x, \ i) + \sum_{l = 1}^L \mu_l s_l(y_i, x,i)] P(y∣x)=Z1exp[i=1∑T(k=1∑Kλktk(yi−1, yi, x, i)+l=1∑Lμlsl(yi,x,i)]=Z1 i=1∏T+1exp[k=1∑Kλktk(yi−1, yi, x, i)+l=1∑Lμlsl(yi,x,i)]
令K=K 1 +K 2 (这里的 K是K1,L是K2)
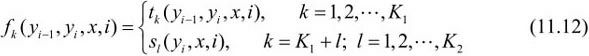
M i ( y i − 1 , y i , x ) = e x p ( W i ( y i − 1 , y i ∣ x ) ) W i ( y i − 1 , y i ∣ x ) = ∑ k = 1 K f k ( y i − 1 , y i , x ) M_i(y_{i-1}, \ y_i, \ x)=exp(W_i(y_{i-1}, \ y_i| x)) \\ W_i(y_{i-1}, \ y_i| x) = \sum_{k=1}^{K}f_k(y_{i-1}, \ y_i, \ x) Mi(yi−1, yi, x)=exp(Wi(yi−1, yi∣x))Wi(yi−1, yi∣x)=k=1∑Kfk(yi−1, yi, x)
因此,条件概率 P w ( y ∣ x ) P_w(y|x) Pw(y∣x)是:
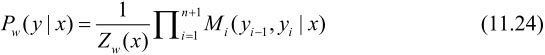
规范化因子 Z w ( x ) Z_w (x) Zw(x)是以start为起点stop为终点通过状态的所有路径 y 1 y 2 … y n y_1 y_2…y_n y1y2…yn 的非规范化 概率![]() 之和。
之和。
对观测序列 x 的每一个位置 i = 1 , 2 , . . . , n + 1 i = 1,2,...,n + 1 i=1,2,...,n+1,由于 y i − 1 y_{i-1} yi−1 和 y i y_i yi 在 m 个标记中取值,所以可以定义一个 m 阶矩阵随机变量.
M i ( x ) = [ M i ( y i − 1 , y i , x ) ] m ∗ m M_i(x) = [M_i(y_{i-1}, \ y_i, \ x)]_{m *m} Mi(x)=[Mi(yi−1, yi, x)]m∗m
这里的 M i M_i Mi 就是隐马尔可夫模型中的状态转移概率矩阵A,但是条件随机场打破了齐次马尔可夫性,即状态转移概率不随时间的变化而变化。这里在不同时间/位置的状态转移概率矩阵是不同的,还有一点就是,HMM中的状态转移概率矩阵是规范化的概率分布,每一行的和为1。而条件随机场是非规范的概率分布,因为并没有计算归一化因子,所以矩阵的每一行的和不为1。
条件随机场的三个问题
和隐马尔可夫模型一样,条件随机场也有三个问题:估计(evaluation),学习(learning),解码(decoding)/预测。