国王游戏
时间限制: 1 Sec 内存限制: 128 MB
题目描述
恰逢H国国庆,国王邀请n 位大臣来玩一个有奖游戏。首先,他让每个大臣在左、右手上面分别写下一个整数,国王自己也在左、右手上各写一个整数。然后,让这n 位大臣排成一排,国王站在队伍的最前面。排好队后,所有的大臣都会获得国王奖赏的若干金币,每位大臣获得的金币数分别是:排在该大臣前面的所有人的左手上的数的乘积除以他自己右手上的数,然后向下取整得到的结果。
国王不希望某一个大臣获得特别多的奖赏,所以他想请你帮他重新安排一下队伍的顺序,使得获得奖赏最多的大臣,所获奖赏尽可能的少。注意,国王的位置始终在队伍的最前面。
输入
第一行包含一个整数n ,表示大臣的人数。
第二行包含两个整数a 和b ,之间用一个空格隔开,分别表示国王左手和右手上的整数。
接下来n 行,每行包含两个整数a 和b ,之间用一个空格隔开,分别表示每个大臣左手和右手上的整数。
输出
输出只有一行,包含一个整数,表示重新排列后的队伍中获奖赏最多的大臣所获得的金币数。
样例输入
复制样例数据
3 1 1 2 3 7 4 4 6
样例输出
2
提示
按1、2、3 号大臣这样排列队伍,获得奖赏最多的大臣所获得金币数为2;
按1、3、2 这样排列队伍,获得奖赏最多的大臣所获得金币数为2;
按2、1、3 这样排列队伍,获得奖赏最多的大臣所获得金币数为2;
按2、3、1 这样排列队伍,获得奖赏最多的大臣所获得金币数为9;
按3、1、2 这样排列队伍,获得奖赏最多的大臣所获得金币数为2;
按3、2、1 这样排列队伍,获得奖赏最多的大臣所获得金币数为9。
因此,奖赏最多的大臣最少获得2 个金币,答案输出2 。
【数据范围】
对于20%的数据,有1≤ n≤ 10,0 < a、b < 8;
对于40%的数据,有1≤ n≤20,0 < a、b < 8;
对于60%的数据,有1≤ n≤100;
对于60%的数据,保证答案不超过 10^9;
对于100%的数据,有 1 ≤ n ≤1,000,0 < a、b < 10000。
证明贪心:
假设有两个橙子A,B,并且到取完A,B后最大的奖赏为S,且前面的人左手乘积为W(左手为l,右手为r):
1.如果A在B的前面,那么S = 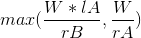 ;
;
2.如果B在A的前面,那么S =  ;
;
那么到底选什么呢?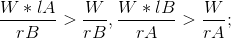 肯定成立,那么就只要比较
肯定成立,那么就只要比较 就行了,我们要求最大值最小,那么,当 lA*rA < lB*rB 时,A在B的前面,正确;当 IB*rB < lA*rA 时,B在A的前面,正确。贪心证明正确。。。。
就行了,我们要求最大值最小,那么,当 lA*rA < lB*rB 时,A在B的前面,正确;当 IB*rB < lA*rA 时,B在A的前面,正确。贪心证明正确。。。。
然后因为n的值有1000,a,b的值有10000,那么可能乘起来有4000位。。。大数相乘。。。。
/**/
#include
#include
#include
#include
#include
#include
#include
![]() 肯定成立,那么就只要比较
肯定成立,那么就只要比较![]() 就行了,我们要求最大值最小,那么,当 lA*rA < lB*rB 时,A在B的前面,正确;当 IB*rB < lA*rA 时,B在A的前面,正确。贪心证明正确。。。。
就行了,我们要求最大值最小,那么,当 lA*rA < lB*rB 时,A在B的前面,正确;当 IB*rB < lA*rA 时,B在A的前面,正确。贪心证明正确。。。。