在某些应用中,要将n个不同的元素分成一组不相交的集合。不相交集合上有两个重要操作,即找出给定的元素所属的集合和合并两个集合。
一:不相交集合的操作
不相交集合教据结构维护一组不相交的动态集合的集合S={S1, S2, ..., SK}。每个集合通过一个代表来识别,代表是集合中的某个成员,在某些应用中,哪一个成员被选作代表是无所谓的,但是必须保证在两次寻找某一集合的代表两次,得到的答案应该是相同的。在另一些应用中,关于如何选择代表可能存在着预先说明的规则,例如选择集合中的最小元素(当然假定集合中的元素是可以排序的)。
集合中的每一个元素是由一个对象表示。设x表示一个对象,希望支持以下操作:
MAKE-SET(x):建立一个新的集合,其唯一成员(因而其代表)就是x。因为各集合是不相交的,故x不会出现在其他集合中。
UNION(x,y):将包含x和y的动态集合Sx和Sy合并为一个新的集合(即这两个集合的并集)。在经过此操作后,原来的集合Sx和 Sy需要从总集合S中删除。
FIND-SET(x):返回一个指针,指向包含x的(唯一)集合的代表。
不相交集合数据结构有多种应用,其中之一是用于确定一个无向图中连通子图,如下图:
求联通子图代码如下,计算过程见上图:
CONNECTED-COMPONENTS对图形进行预处理,然后SAME-COMPONENT回答两个顶点是否在同一个连通分量。
二:不相交集合的链表表示
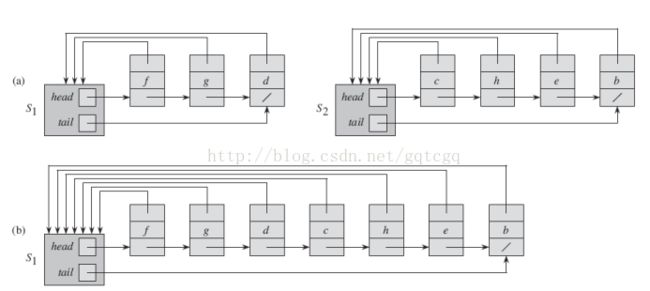
下图给出了实现不相交集合数据结构的简单方法:每个集合用一个自己的链表来表示,每个集合的对象包含head属性和tail属性,head属性指向表的第一个对象,tail指向表的最后一个对象。链表中的每个对象包含一个集合成员,一个指向链表中下一个对象的指针和一个指回到集合对象的指针。链表中的对象以任意的次序出现。
在链表的实现方法中,MAKE-SET操作需要O(1)的时间,只需要创造一个只有x对象的新的链表即可。FIND-SET需要O(1)的时间,仅沿着x对象的返回指针返回到集合对象,然后返回head指向对象的成员。比如在上图(a)中,FIND-SET(g)返回f。
在上图(b)中,体现了UNION(x,y)的结果。利用x所在链表的tail指针,可以迅速的找到拼接y所在的位置,之后,删除y链表即可。但是对于y中的每个对象,需要更新指向集合对象的指针,花费的时间与y所在的链表长度呈线性关系。
如果知道每个表的长度,并且拼接次序可以任意的话,可以总是把较短的表拼接到较长的表中。这叫做加权合并启发式策略。
三:不相交集合森林
在不相交集合的另一种更快的实现中,用有根树来表示集合,树中的每个结点都包含集合的一个成员,每棵树表示一个集合。在一个不相交集合森林中,每个成员仅指向其父结点。每棵树的根包含了集合的代表,并且是它自己的父结点。如下图:
虽然采用了这种表示的算法并不比采用链表表示的算法更快,但是,通过引人两种启发式策略:“按秩合并”和“路径压缩”。就可以获得目前己知的、渐近意义上最快的不相交集合数据结构了。通过同时使用这两种启发式策略,可以获得一个几乎与总的操作数m成线性关系的运行时间。
第一种启发式策略是按秩合并:它与我们用于链表表示中的加权合并启发式是相似的。其思想是使包含较少结点的树的根指向包含较多结点的树的根。我们并不显式地记录每个结点为根的子树的大小,而是对每个结点,用秩表示结点高度的一个上界。在按秩合井中。具有较小秩的根在UNION操作中要指向具有较大秩的根。
第二种启发式即路径压缩。在FIND-SET操作中,利用这种启发式策略,来使查找路径上的每个结点都直接指向根结点。路径压缩并不改变结点的秩。如下图;
为了实现一个按秩合并启发式的不相交集合森林,要记录下秩的变化。对每个结点x,维护一个属性x.rank表示x的高度的一个上界。
当由MAKE-SET创建了一个单元素集合时,对应的树中唯一结点的初始秩为0。每个FIND-SET操作不改变任何秩。当对两棵树应用UNION时,有两种情况,具体取决于根是否有相等的秩。当两个秩不相等时,我们使具有较高秩的根成为具有较低秩的根的父结点。但秩本身保持不变。两个秩相同时.任选一个根作为父结点,并增加其秩的值。代码如下:
过程FIND-SET是一种两越方法,执行完FIND-SET操作后,查找路径上每个结点都直接指向了根。