深入理解Hashtable

一、基本知识

Hashtable它是一个散列表，它存储的内容是键值对映射。

Hashtale继承于Dictionary，实现了Map、Cloneable、Java.io.Serializable接口。

Hashtable的函数是同步的，这意味着它是线程安全的。它的key、value都不可以为null。此外，Hashtable中的映射不是有序的。

二、优势所在

将数据存储在数组中，并通过数组下标搜索会出现两个问题：

1.如果所有元素是16-bits且不带正负号的整数，我们可以用一个拥有65536个元素的arry A，初值全部为0，每个元素值代表相应元素出现的次数（如果插入元素i，就执行A[i]++,如果删除元素i，就执行A[i]--,如果搜查元素i，就检查A[i]是否为0）。于是，不论是插入、删除、搜索每个操作都在常数时间内完成。但是，若元素是32-bits,我们所准备的arry A的大小就必须是2^32 = 4GB，这就大的不太切合实际。

2.如果元素形态是字符串或其他，而非整数，将无法被拿来作为arry的索引。

此问题的解决：

    例如：数值1234是由阿拉伯数字1,2,3,4构成的一样，字符串“jjhou”是由字符‘j’,‘j’，‘h’，‘o’，‘u’构成，那么，既然数值1234是1*10^3+2*10^2+3*10^1+4*10^0,我们也可以将字符编码，每个字符以一个7-bits数值表示（也就是ASCII编码），从而将字符串“jjhou”表现为：

'j'*128^4 + 'j'*128^3 + 'h'*128^2 + 'o'*128^1 + 'u'*128^0

所以，“jjhou”的索引值是：

106*128^4 + 106*128^3 + 104*128^2 + 111*128^1 + 117*128^0 = 28678174709

这是一个非常大的数值，随着字符串长度的增加，数值会更加大，所以这又回归到第一个问题：关于arry的大小。

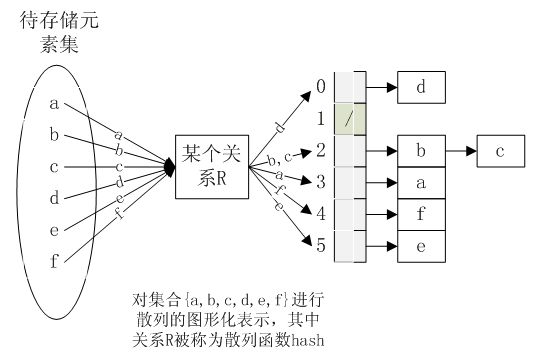
那么，如何避免使用一个大的荒谬的arry呢？办法之一就是使用某种函数映射，将大数映射为小数，负责将某一元素映射为一个“大小可接受的索引”，这样的函数称之为‘散列函数’

三、基本原理

使用一个下标范围比较大的数组来存储元素。可以设计一个函数（哈希函数，也叫散列函数），使得每个元素的关键字都与一个函数值（即数组下标，hash值）相对应，于是用这个数组单元来存储这个元素；也可以理解为，按照关键字为每一个元素分类，然后将这个元素存储在相应类所对应的地方，称为“桶”。但是不能保证每个元素的关键字与函数值是一一对应的，因此极有可能出现对于不同的元素，却计算出了相同的函数值，这样就产生了冲突，换句话说就是把不同的元素分在了相同的类中。总的来说，“直接定址”与“解决冲突”是哈希表的两大特点。

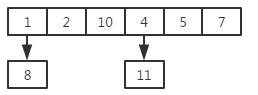
现在有如下几个数：1,2,4,5,7,8,10,11;现在为了方便查找我们可以这样做：

这里的存放规则很简单：

1%7 = 1，放到数组的第一个位置；

2%7 = 2，放到数组的第二个位置；

……

11%7 = 4，放到数组的第四个位置；

这里元素的值对7求余就是所选择的hash函数。如果我们要找数组中是否存在某个数x，可以用x%7求得一个数，这个数就是在这个数组中应该存的位置，此时直接通过这个位置定位数组中的这个元素，就可以很快的判断这个数哎数组中存不存，而不需要一个个遍历数组。

图中可以看到1和8对7求余的余数是相同的，导致他们被放到了同一个位置上，这就是属于冲突的情况。

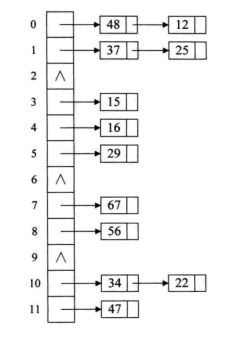
哈希表中解决冲突的方法：

如下图：

除了上述方法外还有

（1）开放寻址发：Hi = （H（key）+ di）MOD m,i=1,2……,K（k<=m-1）.

        ****其中H(key)为散列函数，m为散列表长，di为增量序列，可以有下列三种取法：

                i.di = 1,2,3,...,m-1,称线性探测再散列；

                ii.di = 1^2,-1^2,2^2,-2^2,(3)^2,....,+-(k)^2,(k<=m/2)称二次探测再散列

                iii.di = 伪随机数序列，称为伪随机探测再散列

（2）再散列法：Hi = RHi(key),i=1,2,.....,k RHi均是不同的散列函数，即在同义词产生地址冲突时计算另一个散列函数地址，直到冲突不再发生，这种方法不易产生“聚集”，但增加了计算时间

（3）建立一个公共溢出区。