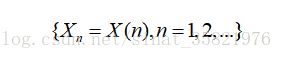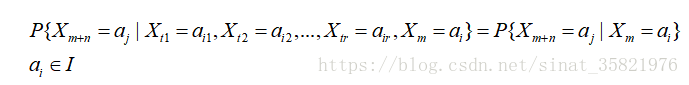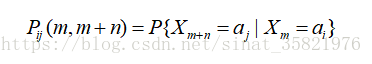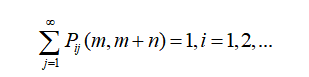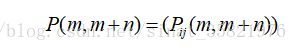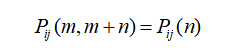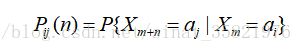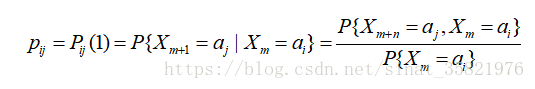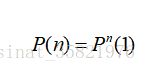一步转移概率矩阵的实现
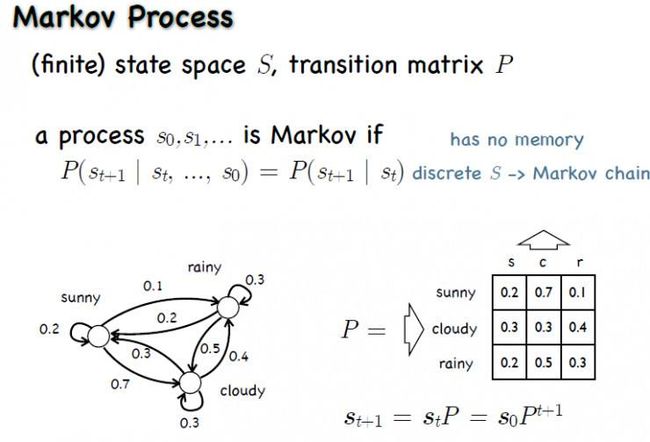
时间和状态都是离散的马尔科夫过程称为马尔科夫链，简称马氏链。记为
它可以看做在时间集
上对离散的马氏过程相继观察的结果。我们约定记链的状态空间为
在链的状态下，马尔科夫性通常用条件分布律来表示，即满足
有
记上式右端为
我们称条件概率
为马氏链在时刻m处于状态ai条件下，在时刻m+n转移到aj的转移概率。
由于链在时刻m从任何一个状态ai出发，到另一时刻m+n，必然转移到a1,a2......诸状态中的某一个,所以
由转移概率组成的矩阵
称为马氏链的转移概率矩阵,由上面的公式知道此矩阵的每一行元素之和等于1.
当转移概率
只与i,j及时间间距n相关时，把它记为
即
并称此转移概率具有平稳性。同时也成此链是齐次的或时齐的。在马氏链在其次的情况下转移概率为
称为马氏链的n步转移概率，当n = 1时为一步转移概率，这是特别重要的。由一步转移概率组成到的矩阵叫一步转移概率矩阵
下面介绍一步转移概率矩阵的实现方法：
1.首先计算每一种状态的概率
2.计算m时刻状态为ai,m+1时刻状态为aj的概率
3.计算转移概率
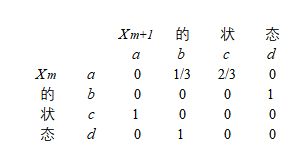
举个例子，有一个序列X= {a,c,a,c,a,b,d,b};
1.首先它的状态空间为I = {a,b,c,d},计算每一种状态的概率 p(a) = 3/8,p(b) = 2/8,p(c) = 2/8,p(d) = 1/8;
2.计算m时刻状态为ai且m+1时刻状态为aj的概率，比如，计算当前时刻为a下一时刻为c的转移概率
由于举的例子状态数比较少很容易知道 p = 1/4;
3.经过上面的计算就可以得出转移概率p(a->c) = p/p(a) = 2/3.
如果上面的过程不好理解，可以用古典概型来计算，为了求p(a->c)可以分别求出当前状态为a时
下一状态为b、c、d的次数：
a->a 0次； a->b 1次；a->c 2次；a->d 0次；
p(a->c)=2/(0+1+2+0)=2/3
为了更好的理解，下面给出序列X的一步转移概率矩阵
如果需要求多步转移概率矩阵，也很简单，对于齐次马氏链而言，n步转移概率矩阵是一步转移概率矩阵的n次方，即
P.S. 马尔科夫一步转移概率矩阵的代码
import operator as op
import numpy as np
x = np.array([1, 3, 1, 3, 1, 2, 4, 2])
count = {}
for i in x[0:len(x) - 1]:
count[i] = count.get(i, 0) + 1
count = sorted(count.items(), key=op.itemgetter(0), reverse=False)
markov_marix = np.zeros([len(count), len(count)])
for j in range(len(x) - 1):
for m in range(len(count)):
for n in range(len(count)):
if x[j] == count[m][0] and x[j + 1] == count[n][0]:
markov_marix[m][n] += 1
for t in range(len(count)):
markov_marix[t, :] /= count[t][1]
print(markov_marix)