pytorch学习 之二 pytorch的一些基础的概念
几个pytorch的基本概念
文章目录
- 几个pytorch的基本概念
- Tensor
- 动态计算图
- 定义自动微分变量
- PyTorch的autograd的简介
- requires_grad属性
- Function类
- backward函数
- autograd的一些其他知识点
- 梯度
Tensor
这个类型是人工智能的重要概念
其实就是一个多维数组,类似numpy里面ndarray

使用张量来进行一些矩阵操作,几乎跟numpy的ndarray一模一样,确实挺方便的。
import torch
x = torch.rand(5,3)
y = torch.ones(5,3)
z = x + y
a = torch.rand(5,3)
print(x)
b = torch.zeros( 5,3,dtype=torch.long )
print(b)
c = torch.tensor([5.5,3])
print(c)
#下面是生成一个类型为double的5,3的矩阵张量,同时,还可以指定类型。
x = x.new_ones( 5,3,dtype=torch.double)
print(x)
y = torch.randn_like(x)
print(y)
x.size()
输出是
tensor([[1.1943, 1.7771, 1.9026],
[1.7972, 1.5472, 1.3902],
[1.0869, 1.4934, 1.1207],
[1.3406, 1.0982, 1.9051],
[1.5109, 1.0314, 1.4367]])
看,几乎跟numpy一样。按照视频教程所说的,numpy中所有关于ndarray的操作都可以用到tensor上,那为什么还要用tensor这个数据类型呢?我们都知道numpy可以被CPU多核加速,而tensor更厉害,它可以被CUDA或者说GPU加速

用上述语句就可以使用CUDA进行矩阵加法,我实际体验,速度还有点慢,这是肯定的,应该是CUDA初始化要消耗时间。
动态计算图
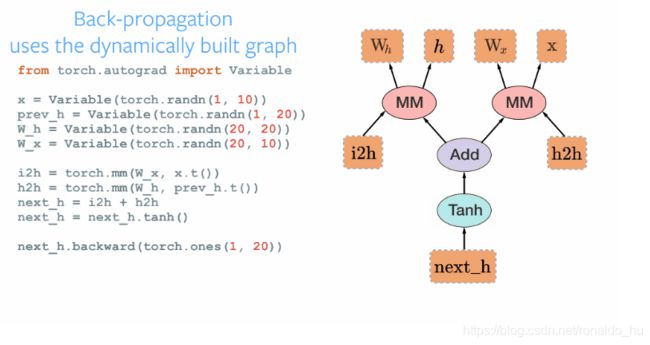
- 动态计算图(Dynamic Computation Graph)是PyTorch的最主要的特性
- 它可以让我们的计算模型更灵活、复杂
- 它可以让反向传播算法随时进行

动态计算图就是一种算法模型。让我们很清晰的构建自己的算法,如上图,椭圆表示pytorch中一系列的计算过程,而方块表示变量,箭头表示依赖关系
定义自动微分变量
这个概念挺有趣的,这也是我之前看不大懂莫烦第一课教程的原因,网上查了一下,准备详细学习一下
在训练一个神经网络的时候,梯度的计算是一个关键的步骤,它为神经网络的优化提供了关键的数据。但是在面临复杂神经网络的时候,导数的计算就会成为一个难题,要求人们解出复杂的、高维的方程式不现实的。这就是自动微分出现的原因,当前最流行的深度学习框架如PyTorch、Tensorflow等都提供了自动微分的支持,让人们只需要少量的工作就能自动计算出复杂函数的梯度
PyTorch的autograd的简介
Tensor是PyTorch实现多维数组计算和自动微分的关键数据结构,一方面,它类似于numpy的ndarray,用户可以对Tensor进行各种数学计算;另一方面,当设置.requires_grad=True之后,在其上进行的各种操作就会被记录下来,用于后续的梯度计算,其内部实现的机制被称为动态计算图.
Variable变量:在pyTorch早期版本中,Tensor只负责多维数组的计算,自动微分的功能是由Variable来完成的。在现在的版本中,二者合二为一了
autograd机制能够记录作用于Tensor上的所有操作,生成一个动态计算图,图的叶子节点是输入的数据,根节点是输出的结果。当在根节点上调用.backward()的时候,就会从根到叶应用链式法则计算梯度。默认情况下,只有.require_grad和is_leaf两个属性都为True的节点才会被计算导数,并存储到grad中。
requires_grad属性
requires_grad属性默认为False,也就是Tensor变量默认是不需要求导的。如果一个节点的requires_grad是True,那么所有依赖它的节点requires_grad也会是True.换而言之,如果一个节点依赖的所有节点都不需要求导,那么它的requires_grad也会是FAlse。在反向传播的过程中,该节点所在的子图会被排除在外。
>>> x = torch.randn(5, 5) # requires_grad=False by default
>>> y = torch.randn(5, 5) # requires_grad=False by default
>>> z = torch.randn((5, 5), requires_grad=True)
>>> a = x + y
>>> a.requires_grad
False
>>> b = a + z
>>> b.requires_grad
True
Function类
我们已经知道PyTorch使用动态计算图(DAG)记录计算的全过程,那么DAG是怎么建立的呢?一些博客认为DAG的节点是Tensor(或说Variable),这其实是不正确的。DAG的节点是Function对象,表示数据依赖,从输出指向输入。因此,Function类在PyTorch自动微分中位居核心地位,但是用户通常不会直接去使用,导致人们对Function类了解并不多。
每当对Tensor施加一个运算的时候,就会产生一个Function对象,它产生运算的结果,记录运算的发生,并且记录运算的输入。Tensor使用.grad_fn属性记录这个计算图的入口。反向传播的过程中,autograd引擎会按照逆序,通过Function的backward依次计算梯度。
backward函数
backward函数是反向传播的入口点,在需要被求导的节点上调用backward函数会计算梯度值到相应的节点上。backward需要一个重要的参数grad_tensor,但如果节点只含有一个标量值,这个参数就可以省略(例如最普遍的loss.backward()与loss.backward(torch.tensor(1))等价),否则就会报如下的错误:
Backward should be called only on a scalar (i.e. 1-element tensor) or with gradient w.r.t. the variable
torch.autograd本质上应该是一个向量-雅克比乘积的计算引擎,计算vT⋅J,而所谓的参数
grad_tensor就是这里的v。由定义容易知道,参数grad_tensor需要与Tensor本身有相同的size。通过恰当地设置grad_tensor,容易计算任意的骗到组合。
反向传播的过程一般用来传递上游传来的梯度,从而实现链式法则,简单的推导如下:

注意梯度是累加的
backward函数本身没有返回值,它计算出来的梯度存放在叶子节点的grad属性中。Pytorch文档中提到,如果grad属性不为空,新计算出来的梯度值会直接加到旧值上面。
为什么不直接覆盖旧的结果呢?这是因为 有些Tensor可能有多个输出,那么就需要调用多个backward。叠加的处理方式使得backward不需要考虑之前有没有被计算过导数,只需要加上去就行了,这使得设计变得更简单,因此我们用户在反向传播之前,常常需要用zero_grad函数对导数进行手动清零,确保计算出来的是正确的结果。
autograd的一些其他知识点
要阻止一个张亮被跟踪历史,可以调用.detach()方法将其与计算历史分离,并阻止它未来的计算记录被跟踪。
为了防止跟踪历史记录(和使用内存),可以将代码块包装在 with torch.no_grad() :中。在评估模型时特别有用,因为模型可能具有requires_grad = True的可训练的参数,但是我们不需要在此过程中队他们进行梯度计算。
还有一个类对于autograd的实现非常重要:Function。
Tensor和Function互相连接生成了一个非循环图,它编码了完整的计算历史。每个张量都有一个.grad_fn属性,它引用了一个创建这个Tensor的Function(除非这个张量是用户手动创建的,即这个张量的grad_fn是None),我的理解是每一个计算的过程都会生成一个新的张量,这个张量的Function就是跟该计算过程相关的.
如果需要计算导数,可以在Tensor上调用.backward()。如果Tensor是一个标量(即它包含一个元素的数据),则不需要为backward()指定任何参数,但是如果它有更多的元素,则需要指定一个gradient参数,它是形状(size)匹配的张量。
例子
x = torch.ones( 2,2,requires_grad=True )
print(x)
输出
tensor(
[[1.,1.],
[1.,1.]], requires_grad=True )
对这个张量做一次运算。
y = x + 2
print(y)
输出
tensor([[3., 3.],
[3., 3.]], grad_fn=)
y是计算的结果,所以它有grad_fn属性。
printf(y.grad_fn)
输出:
猜想这个应该是一个关于加法的function
再对y进行更多的操作
z = y * y * 3
out = z.mean()
print( z,out )
输出:
tensor([[27., 27.],
[27., 27.]], grad_fn=) tensor(27., grad_fn=)
看看,从名字上看z这个张量的对应的grad_fn是一个关于乘法的function,而out是一个关于均值的grad_fn
.requires_grad_(…)可以原地改变现有张量的requires_grad标志。如果没有指定的话,默认输入的这个标志是False。
梯度
因为out是一个标量,所以让我们直接进行反向传播,out.backward()和out.backward(torch.tensor(1.))等价
out.backward()
输出导数d(out)/dx
print(x.grad)
#输出
tensor([[4.5000, 4.5000],
[4.5000, 4.5000]])
数学上,若有向量值函数y = f(x),那么y相对于 x的梯度是一个雅克比矩阵:

通常来说,torch.autograd是计算雅克比向量积的一个“引擎”。也就是说,给定任意向量v =
![]()
计算乘积J.v 。如果v恰好是一个标量函数![]() 即v=
即v=

根据链式法则,雅克比向量积应该是l对x的导数
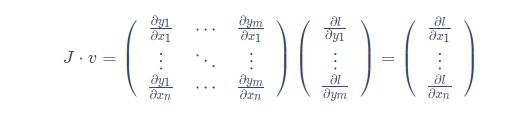
雅克比向量积的这一特性使得将外部梯度输入到具有非标量输出的模型中变得很方便
x =torch.randn(3,requires_grad=True)
y = x*2
while y.data.norm() < 1000:
y = y * 2
print(y)
#上面的y函数是一个标量函数,autograd不能直接计算完整的雅克比矩阵,但是只想要雅克比向量积,只
#需要将这个向量作为参数传给backward
v = torch.tensor( [0.1,1.0,0.001],dtype =torch.float )
y.backward(v)
print(x.grad)