神经网络模型学习笔记（ANN,BPNN）

人工神经网络（Artificial Neural Network，即ANN ），是20世纪80 年代以来人工智能领域兴起的研究热点。它也是目前各种神经网络模型的基础。本文主要对BPNN模型进行学习。

什么是神经网络？

  神经网络是一种运算模型，由大量的节点（或称神经元）之间相互联接构成。每个节点代表一种特定的输出函数，称为激励函数（activation function）。每两个节点间的连接都代表一个对于通过该连接信号的加权值，称之为权重，这相当于人工神经网络的记忆。网络的输出则依网络的连接方式，权重值和激励函数的不同而不同。而网络自身通常都是对自然界某种算法或者函数的逼近，也可能是对一种逻辑策略的表达。

---

目前已有的数十种神经网络模型，目前主要有以下几种类型：前向型、反馈型、随机型和竞争型。

神经网络可分类以下四种类型：

前向型

  前馈神经网络是指神经元分层排列，由输入层，隐藏层和输出层构成，其中隐藏层可能会有多层。这种神经网络的每一层的神经元只接受前一层神经元的输入，后面的层对于前面的层没有信号反馈。每一层对于输入数据进行一定的转换，然后将输出结果作为下一层的输入，直到最后输出结果。

  其中，目前广泛应用的BPNN（Back Propagation Neural Network, 后向传播神经网络）就属于这种网络类型。

反馈型

  反馈网络又称回归网络，输入信号决定反馈系统的初始状态，系统经过一系列状态转移后逐渐收敛于平衡状态，因此，稳定性是反馈网络最重要的指标之一，比较典型的是Hopfield神经网络。

  Hopfield神经网络用于非线性动力学问题分析，已在联想记忆和优化计算中得到成功的应用.

随机型

  具有随机性质的模拟退火(SA)算法解决了优化计算过程陷于局部极小的问题，并已在神经网络的学习及优化计算中得到成功的应用.

竞争型

  自组织神经网络是无教师学习网络，它模拟人脑行为，根据过去经验自动适应无法预测的环境变化，由于无监督，这类网络通常采用竞争原则进行网络学习，自动聚类。目前广泛用于自动控制、故障诊断等各类模式识别中.

---

  这里学习的BPNN就是前向型神经网络的一种。

---

神经元

  为了描述神经网络，我们先从最简单的神经网络讲起，这个神经网络仅由一个“神经元”构成，以下即是这个“神经元”的图示：

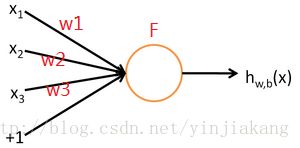
  这个神经元是由x₁，x₂，x₃和一个偏置b = +1 作为输入，w₁，w₂，w₃是他们的权重，输入节点后，经过激活函数F，得到输出。其中函数 被称为“激活函数”。
  这里，我们以sigmoid函数作为激活函数f(x)：

  它的函数图像如下所示：

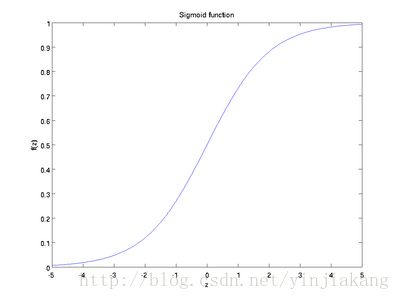
  它的取值范围为 [0, 1]。所以，对于一个神经元来说，整个过程就是，向神经元输入数据，然后经过激活函数，对数据做某种转换，最终得到一个输出结果。

---

神经网络

  所谓神经网络就是将许多个单一“神经元”联结在一起，这样，一个“神经元”的输出就可以是另一个“神经元”的输入。例如，下图就是一个简单的神经网络：

图1

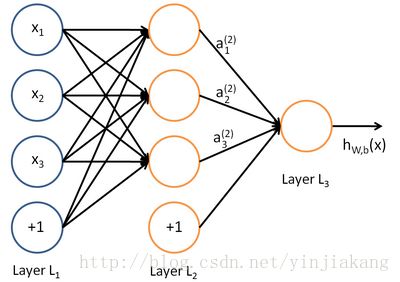
  最左边一层是输入层，中间是隐藏层，右侧是输出层。输入层以及隐藏层均有3个节点，每个节点代表一个神经元。输入层有3个输入节点，x1, x2, x3， 以及一个偏置节点（标有+ 1的圆圈）。每一层和下一层之间对应的也有一个权重矩阵w。

  对于这样一个简单的神经网络来说，我们的整个过程就是，将输入x与权重矩阵w结合，以wx + b的形式输入隐藏层（Layer L₂），经过激活函数f(x)的处理，得到输出结果a1, a2, a3， 然后与对应的权重，偏置结合，作为输出层（Layer L₃）的输入，经过激活函数，得到最终输出结果。

---

  好了，在了解完一些基础的神经网络的网络结构以及计算流程之后。我们来介绍一下本文学习的BPNN模型。

  那什么是BPNN呢？

---

BPNN算法理解及原理

  BPNN全称Back Propagation Neural Network，后向传播神经网络。前文有介绍，他也属于前馈型神经网络的一种。BP神经网络就是在前馈型网络的结构上增加了后向传播算法（Back Propagation）。那它和前馈型神经网络又有什么区别呢？

  我们知道，前馈型神经网络，就像流水一样，从水的源头一路流到尽头，没有倒流。前馈就是信号向前传递的意思。BP网络的前馈表现为输入信号从输入层（输入层不参加计算）开始，每一层的神经元计算出该层各神经元的输出并向下一层传递直到输出层计算出网络的输出结果， 前馈只是用于计算出网络的输出，不对网络的参数进行调整。

  而后向传播是用于训练时网络权值和阈值的调整，该过程是需要监督学习的。在你的网络没有训练好的时候，输出肯定和你想象的不一样，那么我们会得到一个偏差，并且把偏差一级一级向前传递，逐层得到 δ ⁽ⁱ⁾，这就是反馈。

  反馈是用来求偏导数的，偏导数是用来作梯度下降的，梯度下降是为了求得代价函数的极小值，使得期望和输出之间的误差尽可能的减小。

BPNN的算法流程

  下面我们来介绍一下算法流程。如下图所示：

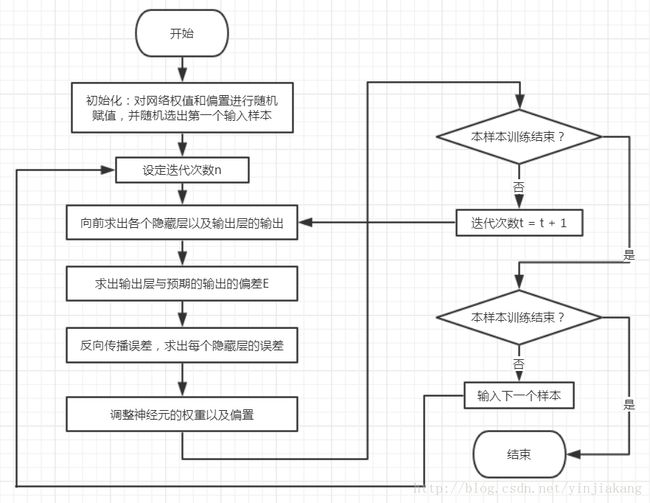
  大致可以分为五个步骤：

  1.初始化网络权重以及偏置。我们知道不同神经元之间的连接权重（网络权重）是不一样的。这是在训练之后得到的结果。所以在初始化阶段，我们给予每个网络连接权重一个很小的随机数（一般而言为-1.0~1.0或者-0.5~0.5），同时，每个神经元有一个偏置（偏置可看做是每个神经元的自身权重)，也会被初始化为一个随机数。

  2.进行前向传播。输入一个训练样本，然后通过计算得到每个神经元的输出。每个神经元的计算方法相同，都是由其输入的线性组合得到。我们以文中神经网络部分中的图1为例：

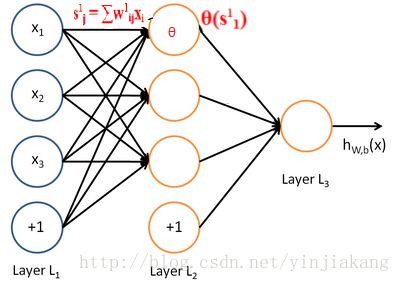
  我们用 Wlij 表示第 l 层的第 i 个节点与第 l+1 层的第 j 个节点之间的权重，其中我们将第 l 层记为L _l ，本图中L₁与L₂层之间的权重即为 W1ij ，L₂与L₃层之间的权重即为 W2ij .。
  我们用 bli 代表第 l+1 层第 i 个节点的偏置项。
  我们用 slj 表示第 l+1 层第 j 个节点的输入值。当 l=1 时， s1j=∑mi=1W1ij⋅xi+b1j 。
  我们 θ(slj) 代表第 l+1 层第 j 个节点经过激活函数 θ(x) 后的输出值。

  那我们可以得到如下公式：

s(1)1s(1)2s(1)3hW,b(x)=W(1)11x1+W(1)21x2+W(1)31x3+b(1)1=W(1)12x1+W(1)22x2+W(1)32x3+b(1)2=W(1)13x1+W(1)23x2+W(1)33x3+b(1)3=θ(s(2)1)=θ(W(2)11θ(s(1)1)+W(2)21θ(s(1)2)+W(2)31θ(s(1)3)+b(2)1)

  这样就完成了一次的训练，我们得到了输出结果 hW,b(x) 。

  3.计算误差并进行反向传播。这也正是这个算法的学习过程。那我们要学习什么呢？当然是希望我们算法的输出能和我们的真实值最大程度的一致了。当我们的输出值与真实值不一致时，必然会产生一个误差，误差越小，也就代表我们算法预测的效果越好。那么什么东西在影响输出？显然，输入的数据是已知的，变量只有那些个连接权重了，那这些连接权重如何影响输出呢？

  我们假设输入层第i个节点到隐层第j个节点的连接权重发生了一个很小的变化 Δwij ，那么这个 Δwij 将会对 sj 产生影响，导致 sj 也出现一个变化 Δsj ，然后产生 Δθ(sj) ，然后传到各个输出层，最后在所有输出层都产生一个误差Δe。所以说，权重的调整将会使得输出结果产生变化，那么如何使这些输出结果往正确方向变化呢？这就是接下来的任务：如何调整权重。

  对于一个给定的样本，我们知道其正确的输出以及神经网络的输出，两者将会产生一个误差，显然误差越小，网络的效果越好。那怎么使得误差做小呢？一般情况下，我们用最小化均方根差来衡量误差大小，公式如下：

L(e)=12SSE=12∑kj=1e2j=12∑kj=1(yj¯¯¯−yj)2

  有了误差，我们如何将其最小化？利用梯度下降的方法。也就是让每个样本的权重都向其负梯度方向变化。也即求误差L对于对于权重W的梯度。

  对于输入层到隐藏层的权重，我们有

∂L∂W1ij=∂L∂s1j∗∂s1j∂W1ij   （1）
  由于
s1j=∑mi=1W1ij⋅xi+b1j   （2）
  所以
∂s1j∂W1ij=xi   （3）
  带入 （1）中可得：
∂L∂W1ij=∂L∂s1j⋅xi   （4）
  然后我们需要求 ∂L∂s1j ，因为所有的 s1j 对于 s2i 都有影响：
s2i=∑nj=1W2ji⋅θ(s1j)+b2i   （5）
  我们可以将 ∂L∂s1j 转化为：
∂L∂s1j=∑ki=1∂L∂s2i⋅∂s2i∂s1j   （6）
  又根据（5），我们得到：
∂s2i∂s1j=∂s2i∂θ(s1j)⋅∂θ(s1j)∂s1j=W2ji⋅θ'(s1j)   （7）
  带入（6）可以得到：
∂L∂s1j=θ'(s1j)∑ki=1∂L∂s2i⋅W2ji   （8）
  现在，我们记
δli=∂L∂sli   （9）
  我们有：
δ1j=θ'(s1j)∑i=1δ2i⋅W2ji   （10）
  因为：

δ2i=∂L∂s2i=∂∑kj=012(yj¯¯¯−yj)2∂s2i=(yi¯¯¯−yi)⋅∂yi¯¯¯∂s2i=ei⋅∂yi¯¯¯∂s2i=ei⋅∂θ(s2i)∂s2i=ei⋅θ′(s2i)

  计算到这一步，我们可以看出来反向传播体现在哪里了，就是 ei 。反向传播时，我们可以将输出层看作输入层，那么这里每个输出层节点的 ei 其实就是我们的输入，经过激活函数 θ′(s2i) ，得到输出层的反向输出 δ2i 。然后将 δ2i 与连接权重结合，作为隐藏层的反向输入，得到隐藏层的反向输出 δ1j ，即：
δ1j=θ'(s1j)∑i=1δ2i⋅W2ji
  有了反向输出后我们就可以计算第一层的权重梯度了：
∂L∂W1ij=δ1j⋅xi
  以及第二层的权重梯度
∂L∂W2ij=∂L∂s2j⋅∂s2j∂W2ij=δ2j⋅θ(s1i)

  我们可以看到一个规律：每一层的权重梯度都等于这一层权重所连的前一层的输入 乘以 所连的后一层的反向输出。 比如输入层与隐藏层之间所连的权重梯度就等于输出层的输入 xi 乘以 隐藏层的反向输出 δ1j ， 也即 δ1j⋅xi 。

  4.网络权重与神经网络元偏置调整。有了权重梯度后，我们就可以很容易的更新我们的权重了.

Wlij=Wlij−α∂L∂Wlij

  5.判断结束。对于每个样本，我们判断其误差如果小于我们设定的阈值或者已经达到迭代次数。我们就结束训练，否则继续回到第二步继续进行训练。

  到此BPNN的训练过程就已结束。训练成熟后的神经网络即可拿来使用。

---

BPNN优缺点

优点：

1. 实现了输入输出的非线性映射。也就是说我们可以利用神经网络来逼近任何一个非线性的连续函数。这非常适合我们在进行数据挖掘时进行多维的特征构造。

2. BP神经网络使用了梯度下降算法。使得我们可以对参数进行优化以减小误差，得到更优的结果。

3. **具有一定的泛化能力。**BP神经网络可以以较少的样本数据来训练生成一个网络，而这个网络能在一定的范围内保证一定的精度。而且BP神经网络的泛化能力是与各种参数有关系的，当新的数据进入网络进行训练的时候，神经网络能够在调整权值以适应更多的数据。

4. 不同的传递函数。与其他神经元模型不同的是，BP神经元模型的传递函数采取了可微单调递增函数，如sigmoid的logsig、tansig函数和线性函数pureline。BP网络的最后一层神经元的特性决定了整个网络的输出特性。当最后一层神经元采用sigmoid类型的函数时，那么整个神经元的输出都会被限制在一个较小的范围内，如果最后一层的神经元采用pureline型函数，则整个网络的输出可以是任意值。

缺点：

1. 局部极小化问题。因为BP神经网络采用的是梯度下降的算法。众所周知，梯度下降有可能会产生局部最小值。而我们需要的是全局最小值。这种特性会使我们的算法陷入局部极值，权值收敛到局部极小点，从而导致网络训练失败。

2. BP 神经网络算法的收敛速度慢。由于BP神经网络算法本质上为梯度下降法，它所要优化的目标函数是非常复杂的，因此，必然会出现“锯齿形现象”，这使得BP算法低效；又由于优化的目标函数很复杂，它必然会在神经元输出接近0或1的情况下，出现一些平坦区，在这些区域内，权值误差改变很小，使训练过程几乎停顿；BP神经网络模型中，为了使网络执行BP算法，不能使用传统的一维搜索法求每次迭代的步长，而必须把步长的更新规则预先赋予网络，这种方法也会引起算法低效。以上种种，导致了BP神经网络算法收敛速度慢的现象。

3. 网络结构的设计。即隐含层的数目以及每个隐含层节点的个数的选择，目前无理论指导;

4. BP神经网络预测能力和训练能力的矛盾问题。预测能力也称泛化能力或者推广能力，而训练能力也称逼近能力或者学习能力。一般情况下，训练能力差时，预测能力也差，并且一定程度上，随着训练能力地提高，预测能力会得到提高。但这种趋势不是固定的，其有一个极限，当达到此极限时，随着训练能力的提高，预测能力反而会下降，也即出现所谓“过拟合”现象。出现该现象的原因是网络学习了过多的样本细节导致，学习出的模型已不能反映样本内含的规律，所以我们在实战中应该把握好度。

---

BP神经网络的应用场景

1.模式识别。

  模式识别通常是指对表征事物或现象的各种形式的(数值的、文字的和逻辑关系的)信息进行处理和分析，以便确定他们属于哪种类别。

2.函数逼近。

  对于一些表达式过于复杂的函数，或者是难以表达的函数，我们可以利用神经网络来无限逼近他们，对他们进行模拟。

3.预测。

  先利用一些已知的数据对网络进行训练，然后再利用这个训练好的网络来对新来的数据进行预测。相比于传统的方法来说，神经网络提高了准确度，并且只需要较少的数据。

4.数据压缩。

  数字图像压缩实际上是以较少的比特数有损或者无损的来表示原来像素矩阵的一种图像处理技术,实际上就是减少图像数据中的时间冗余,空间冗余,频谱冗余等等作为目的,从而同过减少上述的一种或者多种冗余的信息而达到更加高效的存储与传输数据.图像的压缩系统其实无论采用什么样的具体的架构或者技术方法,基本的过程都是一致的,主要还是可以概述为编码,量化,解码这三个部分。

  从理论上讲,编解码问题其实就可以归结为映射与优化的问题,从神经网络的方面来看无非就是实现了从输入到输出的一个非线性的映射关系,并且衡量性能的标准可以从并行处理能力是否高效,容错率是否合适,以及是否具有鲁棒性.分析图像压缩的基本原理其实和上述的BP神经网络的原理一样。所以我们可以利用BP神经网络来解决图像压缩问题。

参与资料及引用内容出处：
http://www.cnblogs.com/chamie/p/5579884.html
http://blog.csdn.net/dengjiexian123/article/details/22829509
http://ufldl.stanford.edu/wiki/index.php/%E7%A5%9E%E7%BB%8F%E7%BD%91%E7%BB%9C
http://blog.csdn.net/zhongkejingwang/article/details/44514073
https://www.zhihu.com/question/22553761
http://blog.csdn.net/heyongluoyao8/article/details/48213345
http://blog.csdn.net/mysteryhaohao/article/details/51386235
http://www.docin.com/p-1625054975.html
http://blog.csdn.net/fengbingchun/article/details/50274471
http://www.jianshu.com/p/f129d1d73a1d