机器学习深度学习基础笔记(3)——Backpropagation算法讲解

• 该系列是笔者在机器学习深度学习系列课程学习过程中记录的笔记，简单粗暴，仅供参考。
• 下面的算法代码来自https://github.com/mnielsen/neural-networks-and-deep-learning
• 再次强调，代码不是笔者自己写的，是从上面的链接下载的！
• 看懂该节内容需要了解一点编程和SVM分类器。

两个识别算法

在开始讲Backpropagation算法前，先讲解两个简单的识别算法：

1.平均灰度衡量

用784个像素点传入神经网络太繁杂，于是改用平均灰度衡量。

平均灰度衡量（Average Darkness）：28×28个像素点的值全部相加然后除以784。10个类别中，每一个类别的灰度平均值都不一样。输入图片后得到的灰度与哪一个类别的灰度平均值接近就判断为那个类别。

• 算法主体

from collections import defaultdict

import mnist_loader

def main():
    training_data, validation_data, test_data = mnist_loader.load_data()
    # training phase: compute the average darknesses for each digit,
    # based on the training data
    avgs = avg_darknesses(training_data)
    # testing phase: see how many of the test images are classified
    # correctly
    num_correct = sum(int(guess_digit(image, avgs) == digit)
                      for image, digit in zip(test_data[0], test_data[1]))
    print "Baseline classifier using average darkness of image."
    print "%s of %s values correct." % (num_correct, len(test_data[1]))

解释：
training_data, validation_data, test_data = mnist_loader.load_data()：通过load_data()方法获取 training_data, validation_data, test_data 三个数据集
avgs = avg_darknesses(training_data)：training_data计算图片平均灰度值
num_correct ：统计算对了多少图

• 求平均灰度

def avg_darknesses(training_data):
    """ Return a defaultdict whose keys are the digits 0 through 9.
    For each digit we compute a value which is the average darkness of
    training images containing that digit.  The darkness for any
    particular image is just the sum of the darknesses for each pixel."""
    digit_counts = defaultdict(int)
    darknesses = defaultdict(float)
    for image, digit in zip(training_data[0], training_data[1]):
        digit_counts[digit] += 1
        darknesses[digit] += sum(image)
    avgs = defaultdict(float)
    for digit, n in digit_counts.iteritems():
        avgs[digit] = darknesses[digit] / n
    return avgs

解释：
digit_counts：定义一个defaultdict变量，下标对应类别0~9，存储的值为每个类别的平均灰度值。
digit：0~9
digit_counts：类别key
darknesses：灰度value
sum(image)：灰度值总和
iteritems()：输出字典的键值对，就是key和value
avgs[digit]：digit类别所有图片的灰度平均值

• 判断(识别)类别

def guess_digit(image, avgs):
    """Return the digit whose average darkness in the training data is
    closest to the darkness of ``image``.  Note that ``avgs`` is
    assumed to be a defaultdict whose keys are 0...9, and whose values
    are the corresponding average darknesses across the training data."""
    darkness = sum(image)
    distances = {k: abs(v-darkness) for k, v in avgs.iteritems()}
    return min(distances, key=distances.get)

if __name__ == "__main__":
    main()

解释：
darkness：一张图片(输入的图片)的灰度值总和
abs()：求绝对值
distances：每个类别的平均灰度值减去输入图片的灰度值的绝对值——距离，存入dict中
min(distances, key=distances.get)：返回灰度距离最小的key
运行结果：

2225 of 10000 values correct

也就是说，准确率达到了22.25%，相比较随机猜测的10%概率而言，有所提高，不过还是然并卵。

2.SVM

代码如下：

import mnist_loader 

from sklearn import svm

def svm_baseline():
    training_data, validation_data, test_data = mnist_loader.load_data()
    # train
    clf = svm.SVC()
    clf.fit(training_data[0], training_data[1])
    # test
    predictions = [int(a) for a in clf.predict(test_data[0])]
    num_correct = sum(int(a == y) for a, y in zip(predictions, test_data[1]))
    print "Baseline classifier using an SVM."
    print "%s of %s values correct." % (num_correct, len(test_data[1]))

if __name__ == "__main__":
    svm_baseline()

clf = svm.SVC()：导入SVM分类器
clf.fit(training_data[0], training_data[1])：学习训练，PS：training_data[0]是输入x，training_data[1]是类别y。
predictions：输入测试集图片，把判断类别的结果存到a里面。
num_correct：识别对了多少图片。
运行结果：

9435 of 10000 values correct.

也就是说，准确率达到了94.35%。

以上就是两个不同分类器识别准确率的对比。

Backpropagation

Backpropagation于1970年被提出

Backpropagation算法核心解决的问题：针对cost函数C，计算 ∂C∂w和∂C∂b

特殊标记

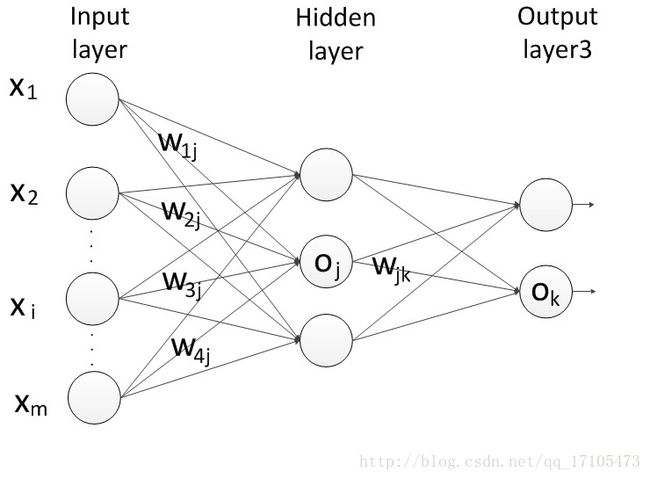
进入正题前先说明一下特殊标记(以下图为例)：

权重的标记： wljk
l：第l层和l-1层之间
j：第l-1层的第j个神经元
k：第l层的第k个神经元

偏移量的标记： blj
l：第l层(b所在层)
j：第j个神经元

同理，激活值： alj=σ(∑kwljkal−1j+blj)
eg： a31=σ(∑kw31ka21+b31)
就是把第2层所有神经元激活值进行 σ() 运算之后累加起来。

简单概括一下，就是两步：
①wa+b；②sigmoid函数

对于每一层(l)定义一个weight matrix权重矩阵： wl
wl ：每一层一个 wl 矩阵（这里的层是两层之间）
例如： w3 就是第2层和第三层之间的所有权重放入 w3 矩阵中。

wljk ：连接l和l-1层之间，矩阵 第j行、第k列 的元素。

对于每一层(l)定义一个bias vector偏移向量： bl
bl ：每一层一个 bl 向量（这里的层就是层）
blj ：第l层、第j个元素

同理，对于每一次(l)的激励值： al ， alj

al=σ(zl)=σ(wlal−1+bl)
alj=σ(∑kwljkal−1j+blj)
用矩阵和向量表示会简单很多，对于每一层，只需要乘以权重矩阵再加上偏移向量就可以了

中间变量： zl ， zlj

zl≡wlal−1+bl
zlj=∑kwljkal−1j+blj

---

详解：
vectorizing a function(向量化一个方程)
σ(v)j=σ(vj)
例如：f(x)= x2

f([23])=[f(2)f(3)]=[49]

---

关于Cost函数的两个假设：

• 回顾Cost函数：

C=12n∑x∥∥y(x)−aL(x)∥∥2
n：所有训练实例的个数
x：训练实例
y(x)：每一个训练实例对应的标签，实际的标签
L：是输出层的层数
aL(x) ：最后输出的值，预测得标签
求和是对于所有单个的训练实例x加起来，然后求平均Cost

假定1：Cost函数可以写成如下形式
平均Cost： C=1n∑xCx
对于单个x的Cost： Cx=12∥∥y−aL∥∥2

因为对于Backpropagation， ∂C∂w和∂C∂b 的计算是通过单个实例x完成的。

Cost可以被写成神经网络输出的一个函数。

1.我们定义的这个二次cost方程满足这点：
Cx=12∥∥y−aL∥∥2=12∑j(yj−aLj)2

2.The Hadamard product，s⊙t
对应元素分别相乘
[1 2]⊙[34]=[1∗32∗4]=[38]

Backpropagation的四个关键公式：

首先定义一个量，表示误差error： δlj （l：第几层，j：第几个神经元）

然后定义一个变量： Δzlj
把它加入到sigma中，使本来的输出 σ(zlj) ，变为 σ(zlj+Δzlj) （每一个神经元多加了一个量），最终造成Cost变为： ∂C∂ΔzljΔzlj

假设现在通过找到一个 Δzlj 来降低cost，
如果 ∂C∂zlj 太大，通过找到合适的 Δzlj 来降低cost；如果cost接近0，就无法改进太多，接近最优，所以 ∂C∂zlj 可以作为一个error的一个衡量

于是，我们定义： δlj≡∂C∂zlj

• 第一个重要的公式：

一个对于error在输出层的方程：

δLj=∂C∂aljσ′(zlj)

等式右边第一项 ∂C∂alj 衡量Cost变化对于第j个activation输出（第j个activation值的变化引起的Cost变化）。我们理想的情况是，C不因为某一个特定的输出神经元而变化太大，所以error就比较小。
等式右边第二部分 σ′(zlj) 是衡量activation方程变化对于中间变量 (zlj 的变化

δLj 转化为矩阵的表达方式（第一个关键公式）：

δL=▽aC⊙σ′(zL)

▽aC ：是根据输出层activation变化而变化的变化率， ▽aC=(aL−y) 。

对于二次Cost方程：

δL=(aL−y)⊙σ′(zL)

一个因下一层error变化引起的当前层error变化的方程（第二个关键公式）：

δl=((wl+1)Tδl+1)⊙σ′(zL)

第l层的下一层的权重矩阵的转置 乘以 第l层的下一层的error，理解为error往回传递，再求与 ⊙σ′(zL) 的Hadamard product，计算出对于l层的error

交替使用：

δLj=∂C∂aljσ′(zlj)

和

δl=((wl+1)Tδl+1)⊙σ′(zL)

δLj=∂C∂aljσ′(zlj) 得出输出层的误差
δl=((wl+1)Tδl+1)⊙σ′(zL) 得出往前一层的误差

这样交替使用这两个公式就可以得出所有神经网络中每一层每一个神经元对应的的误差。

一个关于cost变化率根据偏向bias的方程（第三个关键公式）：

∂C∂blj=δlj

简化：

∂C∂b=δ

一个关于cost变化率根据权重weight的方程（第四个关键公式）：

∂C∂wljk=al−1kδlj

简化：

∂C∂w=ainδout

就是说，根据a和error来求偏导 ∂C∂w
当 ain 很小时，偏导数也很小，所以权重更新会慢(学习的慢)，结论就是：从low activation来更新权重，学习过程会比较慢

根据 δLj=∂C∂aljσ′(zlj) 和sigmoid函数的图像

可以看出，函数值接近1或者0的时候，曲线都很平，说明 σ′(zlj 接近0，结论就是：当输出层的权重学习比较慢，如果输出层的activation很高或很低时，对于bias也一样。

• 总结四个方程：

BP1：输出层的error

δL=▽aC⊙σ′(zL)

BP2：除了输出层的error外，其它每一层的error

δl=((wl+1)Tδl+1)⊙σ′(zL)

BP3：bias的偏导

∂C∂blj=δlj

BP4：weight的偏导

∂C∂wljk=al−1kδlj

Backpropagation 算法数学形式步骤：

1.输入x：设置输入层activation a

2.正向更新：对于l=1,2,3,4，……，L计算

• zl=wlal−1+bl
• al=σ(zl)

3.计算出输出层error

• δL=▽aC⊙σ′(zL)

4.反向更新error（Backpropagate error)

• δl=((wl+1)Tδl+1)⊙σ′(zL)

5.输出

• ∂C∂wljk=al−1kδlj
• ∂C∂blj=δlj

Backpropagation 算法总体思路：

1.迭代处理训练集中的实例
2.对比经过神经网络输入层预测值（predicted value)与真实值（target value）之间
3.反方向（从输出层=>隐藏层=>输入层）以最小化误差（error）来更新每个连接的权重（weight）
4.算法详细介绍

• 输入：D：数据集，l：学习率（learning rate），一个多层前向神经网络
• 输出：一个训练好的神经网络（a trained
  neural network）

(1)初始化权重（weight)和偏向bias：随机初始化在-1到1之间。或者-0.5到0.5之间，每个单元有一个偏向
(2)对于每一个训练实例X，执行以下步骤（下面的公式用了别的符号来表达）：
①由输入层向前传递

Ij=∑iwijOi+θj
I ：就是中间变量z

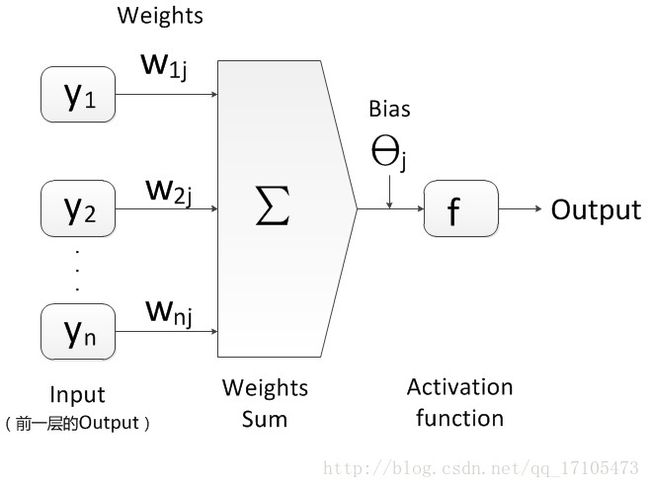
下一层神经元的值：
Oj=11+e−Ij

②根据误差error反向传递

• 对于输出层：

Errj=Oj(1−Oj)(Tj−Oj)

Errj 就是前面关键公式1中的 δL
(Tj−Oj) 就是前面关键公式1中的 ▽aC ； Tj 是真实值， Oj 是预测值
Oj(1−Oj) 就是前面关键公式1中的 σ′(zL)

前面关键公式1： δL=▽aC⊙σ′(zL)

• 对于隐藏层：

Errj=Oj(1−Oj)∑kErrkwjk

∑kErrkwjk 就是前面关键公式2中的 ((wl+1)Tδl+1)

前面关键公式2： δl=((wl+1)Tδl+1)⊙σ′(zL)

• 权重更新：

Δwij=(l)ErrjOi

wij=wij+Δwij

(l) 就是学习率
Errj 就是前面关键公式4中的 δlj
Oj 就是前面关键公式4中的 al−1k
前面关键公式4： ∂C∂wljk=al−1kδlj

• 偏向更新：

Δθj=(l)Errj

θj=θj+Δθj

前面关键公式3： ∂C∂blj=δlj

(3)终止条件有三种：
①权重的更新低于某个阈值，学习结束
②预测得错误率低于某个阈值，学习结束
③达到预设定的循环次数，学习结束

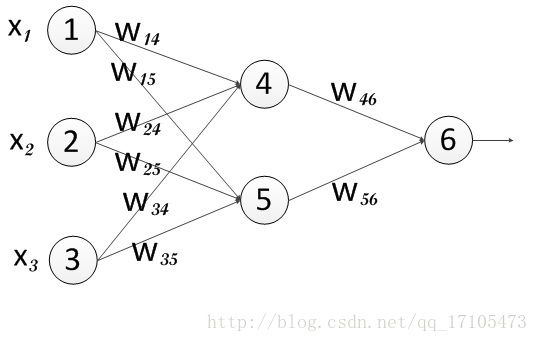
Backpropagation 算法举例：

• 随机给定

输入分别是：
x1 =1
x2 =0
x3 =1
权重分别是：
w14 =0.2
w15 =-0.3
w24 =0.4
w25 =0.1
w34 =-0.5
w35 =-0.2
w46 =-0.3
w56 =-0.2
偏向分别是：
θ4 =-0.4
θ5 =0.2
θ6 =0.1

• 正向传播的计算为：

Unit j	Net input , Ij	output , Oj
4	0.2+0-0.5-0.4=-0.7	11+e0.7=0.332
5	-0.3+0+0.2+0.2=0.1	11+e−0.1=0.525
6	(-0.3)(0.332)-(0.2)(0.525)+0.1=-0.105	11+e0.105=0.474

上表中第二行数据的计算如下：
j=4时，
I4=(w14O1+θ4)+(w24O2+θ4)+(w34O3+θ4)=0.2+0−0.5−0.4=−0.7
O4=11+e−I4=11+e0.7=0.332

• 反向更新的计算为：

输出层： Errj=Oj(1−Oj)(Tj−Oj)

隐藏层： Errj=Oj(1−Oj)∑kErrkwjk

权重更新：
wij=wij+Δwij
Δwij=(l)ErrjOi

偏向更新：
θj=θj+Δθj
Δθj=(l)Errj

---

–计算error：

6是输出层，所以使用第一个公式代入运算
Err6=O6(1−O6)(T6−O6)=0.474(1−0.474)(1−0.474)
4和5是隐藏层，所以使用第二个公式代入运算
Err5=O5(1−O5)Err6w56=0.525(1−0.525)(0.1311)(−0.2)
计算得出下表：

Unit j	Errj
6	(0.474)(1-0.474)(1-0.474)=0.1311
5	(0.525)(1-0.525)(0.1311)(-0.2)=-0.0065
4	(0.332)(1-0.332)(0.1311)(-0.2)=-0.0087

---

–权重更新和偏向更新：

令学习率 (l)=(0.9) ，则

w46=w46+Δw46=w46+(l)Err6O4=−0.3+(0.9)(0.1311)(0.332)=−0.261

计算得出下表：

Unit j	Errj
w46	-0.3+(0.9)(0.1311)(0.332)=-0.261
w56	-0.2+(0.9)(0.1311)(0.525)=-0.138
w14	0.2+(0.9)(-0.0087)(1)=-0.192
w15	-0.3+(0.9)(0.0065)(1)=-0.306
w24	0.4+(0.9)(-0.0087)(0)=0.4
w25	0.1+(0.9)(-0.0065)(0)=0.1
w34	-0.5+(0.9)(-0.0087)(1)=-0.508
w35	0.2+(0.9)(-0.0065)(1)=0.194
θ6	0.1+(0.9)(0.1311)=0.218
θ5	0.2+(0.9)(-0.0065)=0.194
θ4	-0.4+(0.9)(-0.0087)=-0.408

如此往复就可以不断更新权重和偏向。

• 最后提一下，这个是笔者的听课学习笔记，简单粗暴，仅供参考，如有错误，欢迎指正，谢谢。
• 下一节将是关于Backpropagation算法的实现。