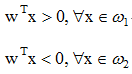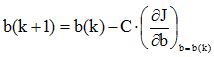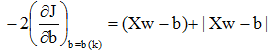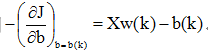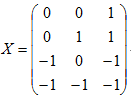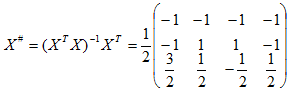判别函数(六)之最小平方误差(LMSE)算法
即使在模式可分的情况下,也很难事先算出达到收敛时所需要的迭代次数。这样,在模式分类过程中,有时候会出现一次又一次迭代却不见收敛的情况,白白浪费时间。为此需要知道:发生迟迟不见收敛的情况时,到底是由于收敛速度过慢造成的呢,还是由于所给的训练样本集不是线性可分造成的呢?最小平方误差(LMSE)算法,除了对可分模式是收敛的以外,对于类别不可分的情况也能指出来。
分类器的不等式方程
求两类问题的解相当于求一组线性不等式的解,因此,若给出分别属于ω1和ω2的两个模式样本的训练样本集,即可求出其权向量w的解,其性质应满足:
其中,0是零向量, 是第i个n维模式样本的增广向量,即
H-K算法:
H-K算法是求解Xw=b,式中b=( b1, b2,…, bn)T,b的所有分量都是正值。这里要同时计算w和b,我们已知X不是N*N的方阵,通常是行多于列的N*(n+1)阶的长方阵,属于超定方程,因此一般情况下,Xw=b没有唯一确定解,但可求其线性最小二乘解。
设Xw=b的线性最小二乘解为w*,即使||Xw*-b||=极小
采用梯度法,定义准则函数:
当Xw=b的条件满足时,J达到最小值。由于上式中包括的![]() 项为两个数量方差的和,且我们将使其最小化,因此也称之为最小均方误差算法。
项为两个数量方差的和,且我们将使其最小化,因此也称之为最小均方误差算法。
使函数J同时对变量w和b求最小。对于w的梯度为:
使![]() ,得XT(Xw-b)=0,从而XTXw=XTb。因为XTX为(n+1)*(n+1)阶方阵,因此可求得解:
,得XT(Xw-b)=0,从而XTXw=XTb。因为XTX为(n+1)*(n+1)阶方阵,因此可求得解:
w = (XTX)-1XTb= X#b
这里X#= (XTX)-1XT称为X的伪逆,X是N*(n+1)阶的长方阵。
由上式可知,只要求出b即可求得w。利用梯度法可求得b的迭代公式为:
根据上述约束条件,在每次迭代中,b(k)的全部分量只能是正值。由J的准则函数式,J也是正值,因此,当取校正增量C为正值时,为保证每次迭代中的b(k)都是正值,应使为非正值。在此条件下,准则函数J的微分为:
该式满足以下条件:
若[Xw(k) – b(k)]> 0,则
若[Xw(k) – b(k)]< 0,则
由b的迭代式和微分,有:
b(k+1) = b(k) +δb(k)
δb(k) = C[Xw(k) –b(k) + | Xw(k) – b(k)|]
将此式代入w=X#b,有:
w(k+1) = X#b(k+1)= X#[b(k) +δb(k)] = w(k) + X#δb(k)
为简化起见,令e(k) = Xw(k) – b(k),可得H-K算法的迭代式。
设初值为b(1),其每一分量均为正值,则:
w(1) = X#b(1)
e(k) =Xw(k) – b(k)
w(k+1) = w(k) + X#{C[Xw(k)– b(k) + |Xw(k) – b(k)|]}
= w(k) + CX#[e(k) + |e(k)|]
由于
X#e(k)= X#[Xw(k) – b(k)] = (XTX)-1XT[Xw(k)– b(k)]
= w(k) –X#b(k) = 0
因此
w(k+1)= w(k) + CX#|e(k)|
b(k+1)= b(k) + C[Xw(k) – b(k) + |Xw(k) – b(k)|]
= b(k) + C[e(k) + |e(k)|]
模式类别可分性的判别
当不等式组Xw>0有解时,该算法对收敛,可求得解w。
(i) 若e(k)=0,即Xw(k)=b(k)>0,有解。
(ii) 若e(k)>0,此时隐含的条件,有解。若继续进行迭代,可使e(k)->0。
(iii) 若e(k)的全部分量停止变为正值(但不是全部为零),表明该模式类别线性不可分。因此,若e(k)没有一个分量为正值,则b(k)不会再变化,所以不能求得解。
l LMSE算法实例
1.有解情况:已知模式样本集:ω1: {(0 0)T, (0 1)T},ω2: {(1 0)T, (1 1)T};模式的增广矩阵X为:
其伪逆矩阵为:
取b(1)=(1 1 1 1)T和C=1,由H-K算法的迭代式:
w(1)=X#b(1)=(-2 0 1)T
因Xw(1)=(1 1 1 1)T,即e(1)= Xw(1)-b(1)= (0 0 0 0)T,故w(1)是解。
2.无解情况
已知模式样本集:ω1: {(0 0)T, (1 1)T},ω2: {(0 1)T, (1 0)T};模式的增广矩阵X为:
其伪逆矩阵为:
取b(1)=(1 1 1 1)T和C=1,由H-K算法的迭代式:
w(1)=X#b(1)=(0 0 0)T
则:e(1)= Xw(1)-b(1)= (-1 -1 -1 -1)T,全部分量均为负,无解。LMSE算法:相对复杂,需要对XTX求逆(维数高时求逆比较困难),但对两类情况,提供了线性可分的测试特征。