Tensorflow2 自动求导机制

https://tf.wiki/zh/basic/basic.html

TensorFlow 引入了 tf.GradientTape() 这个 “求导记录器” 来实现自动求导

如何使用 tf.GradientTape() 计算函数 y(x) = x^2 在 x = 3 时的导数：

import tensorflow as tf

x = tf.Variable(initial_value=3.) #初始化一个tensor x，因求x=3的导数，因此初值为3
with tf.GradientTape() as tape:  # 在 tf.GradientTape() 的上下文内，所有计算步骤都会被记录以用于求导
    y = tf.square(x)  #在with上下文内 写计算式

#with上下文之外
y_grad = tape.gradient(y, x)        # 计算y关于x的导数
print([y, y_grad])

只要进入了 with tf.GradientTape() as tape 的上下文环境，则在该环境中计算步骤都会被自动记录。比如在上面的示例中，计算步骤 y = tf.square(x) 即被自动记录。离开上下文环境后，记录将停止，但记录器 tape 依然可用，因此可以通过 y_grad = tape.gradient(y, x) 求张量 y 对变量 x 的导数。

以下代码展示了如何使用 tf.GradientTape() 计算函数

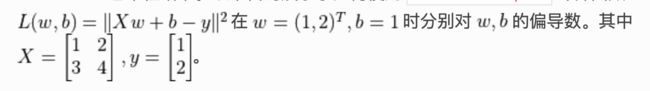
X = tf.constant([[1., 2.], [3., 4.]])   #shape(2, 2)
y = tf.constant([[1.], [2.]])           #shape(2, 1)
w = tf.Variable(initial_value=[[1.], [2.]])   #shape(2, 1)
b = tf.Variable(initial_value=1.)       #shape(1)  矩阵加法的时候用了broadcast机制
with tf.GradientTape() as tape:
    L = 0.5 * tf.reduce_sum(tf.square(tf.matmul(X, w) + b - y))
    
w_grad, b_grad = tape.gradient(L, [w, b])        # 计算L(w, b)关于w, b的偏导数
print([L.numpy(), w_grad.numpy(), b_grad.numpy()])

实现 线性回归

使用 tape.gradient(ys, xs) 自动计算梯度；  
#单纯求导数，返回值是一个tensor。ys一般是loss，xs一般是需要更新的variables。ys分别对variables中每一个参数求导数
使用 optimizer.apply_gradients(grads_and_vars) 自动更新模型参数。
#grads_and_vars=[(grad, x)] 输入参数(gradient,variable) 每一个grad和variable以元组形式输入  一般 grads_and_vars=zip(grads, variables)

import tensorflow as tf


#设置随机数据
x = tf.range(10)
y = tf.range(10,)

x = tf.cast(x, dtype=tf.float32)  #转为float
y = 2 * tf.cast(y, dtype=tf.float32) + tf.random.normal([10,])  #增加随机扰动[10,]表示shape

#参数初始化
w = tf.Variable(initial_value=0.)  
b = tf.Variable(initial_value=0.)
#定义优化器
optimizer = tf.keras.optimizers.Adam(lr=0.05)   
#需要更新的参数
variables = [w, b]

for _ in tf.range(500):

    with tf.GradientTape() as tape:
        L = tf.reduce_mean(tf.square(tf.multiply(w,x) + b - y))  #loss

    L_gradx = tape.gradient(L, variables) #针对loss和需要更新参数求梯度
    optimizer.apply_gradients(grads_and_vars=zip(L_gradx, variables))  #针对（梯度和参数） 进行参数更新

    tf.print([L])  #打印loss

在这里，我们使用了前文的方式计算了损失函数关于参数的偏导数。同时，使用 tf.keras.optimizers.SGD(learning_rate=1e-3) 声明了一个梯度下降 优化器 （Optimizer），其学习率为 0.05。优化器可以帮助我们根据计算出的求导结果更新模型参数，从而最小化某个特定的损失函数，具体使用方式是调用其 apply_gradients() 方法。

注意到这里，更新模型参数的方法 optimizer.apply_gradients() 需要提供参数 grads_and_vars，即待更新的变量（如上述代码中的 variables ）及损失函数关于这些变量的偏导数（如上述代码中的 grads ）。具体而言，这里需要传入一个 Python 列表（List），列表中的每个元素是一个 （变量的偏导数，变量） 对。比如上例中需要传入的参数是 [(grad_a, a), (grad_b, b)] 。我们通过 grads = tape.gradient(loss, variables) 求出 tape 中记录的 loss 关于 variables = [a, b] 中每个变量的偏导数，也就是 grads = [grad_a, grad_b]，再使用 Python 的 zip() 函数将 grads = [grad_a, grad_b] 和 variables = [a, b] 拼装在一起，就可以组合出所需的参数了。