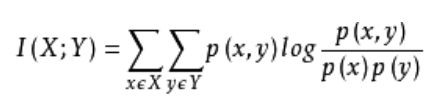机器学习笔记八——特征工程之特征选择
特征选择
- 1、概述
- 2、特征选择过程
- 3、特征选择方法
-
- 3.1 过滤式(filter)特征选择
-
- 3.1.1 Pearson相关系数法
- 3.1.2卡方经验
- 3.1.3 互信息法
- 3.1.4 方差选择法
- 3.2包裹式(wrapper)特征选择
-
- 3.2.1 递归特征消除法
- 3.3 嵌入式(Embedded)特征选择
-
- 3.3.1 基于惩罚项的特征选择法
- 3.3.2 基于学习模型的特征选择
1、概述
1、为什么要进行特征选择?
在现实生活中,一个对象往往具有很多属性(以下称为特征),这些特征大致可以被分成三种主要的类型:
相关特征: 对于学习任务(例如分类问题)有帮助,可以提升学习算法的效果;
无关特征:对于我们的算法没有任何帮助,不会给算法的效果带来任何提升;
冗余特征: 不会对我们的算法带来新的信息,或者这种特征的信息可以由其他的特征推断出;
进行特征选择的主要目的:
-
降维: 属性或者特征过多会造成维数过多问题,如果可以选择重要的特征,使得仅需要一部分特征就可以构建模型,可以大大减轻维数灾难问题,从这个意义上讲,特征选择和降维技术有相似的动机,事实上它们也是处理高维数据的两大主流技术。
-
降低学习任务的难度 去除无关特征可以降低学习任务的难度,也同样让模型变得简单,降低计算复杂度。
-
提升模型的效率
2、特征选择是什么?
特征选择是特征工程里的一个重要问题。
特征选择是选取原始特征集合的一个有效子集,使得基于这个特征子集训练出来的模型准确率最高。简单地说,特征选择就是保留有用特征,移除冗余或无关的特征。
2、特征选择过程
1、特征选择最重要的是确保不丢失重要的特征, 否则就会因为缺少重要的信息而无法得到一个性能很好的模型。
-
给定数据集,学习任务不同,相关的特征很可能也不相同,因此特征选择中的不相关特征指的是与当前学习任务无关的特征。
-
有一类特征称作冗余特征(redundant feature),它们所包含的信息可以从其他特征中推演出来。
-
冗余特征通常都不起作用,去除它们可以减轻模型训练的负担;
-
但如果冗余特征恰好对应了完成学习任务所需要的某个中间概念,则它是有益的,可以降低学习任务的难度。
2.在没有任何先验知识,即领域知识的前提下,要想从初始特征集合中选择一个包含所有重要信息的特征子集,唯一做法就是遍历所有可能的特征组合。
但这种做法并不实际,也不可行,因为会遭遇组合爆炸,特征数量稍多就无法进行。
一个可选的方案是:
-
产生一个候选子集,评价出它的好坏。
-
基于评价结果产生下一个候选子集,再评价其好坏。
-
这个过程持续进行下去,直至无法找到更好的后续子集为止。
对于一个有N个特征的对象,可以产生2^N个特征子集,特征选择就是从这些子集中选出对于特定任务最好的子集。特征选择主要包括四个过程:
- 生成过程: 生成候选的特征子集也就是子集搜索的过程;
- 评价函数:评价特征子集的好坏;
- 停止条件: 决定什么时候该停止;
- 验证过程: 特征子集是否有效;
子集搜索方法步骤如下:
-
给定特征集合 A={A1,A2,…,Ad} ,首先将每个特征看作一个候选子集(即每个子集中只有一个元素),然后对这 d 个候选子集进行评价。
-
假设 A2 最优,于是将 A2 作为第一轮的选定子集。
-
然后在上一轮的选定子集中加入一个特征,构成了包含两个特征的候选子集。
-
假定 A2,A5 最优,且优于 A2 ,于是将 A2,A5 作为第二轮的选定子集。
-
….
-
假定在第 k+1 轮时,本轮的最优的特征子集不如上一轮的最优的特征子集,则停止生成候选子集,并将上一轮选定的特征子集作为特征选择的结果。
1、这种逐渐增加相关特征的策略称作前向 forward搜索
2、类似的,如果从完整的特征集合开始,每次尝试去掉一个无关特征,这种逐渐减小特征的策略称作后向backward搜索
3、也可以将前向和后向搜索结合起来,每一轮逐渐增加选定的相关特征(这些特征在后续迭代中确定不会被去除),同时减少无关特征,这样的策略被称作是双向bidirectional搜索。
4、子集评价
给定数据集 D,假设所有属性均为离散型。对属性子集 A,假定根据其取值将 D 分成了 V 个子集:
D 1 , D 2 , D 3 , . . . , D V D_1,D_2,D_3,...,D_V D1,D2,D3,...,DV
可以计算属性子集 A 的信息增益:
g ( D , A ) = H ( D ) − H ( D ∣ A ) = H ( D ) − ∑ v = 1 V ∣ D V ∣ ∣ D ∣ H ( D V ) g(D,A)=H(D)-H(D|A)=H(D)-\sum_{v=1}^V\frac{|D_V|}{|D|}H(D_V) g(D,A)=H(D)−H(D∣A)=H(D)−∑v=1V∣D∣∣DV∣H(DV)
其中H(D)为信息熵,计算公式如下:
H ( D ) = − ∑ v = 1 V ∣ D V ∣ ∣ D ∣ l o g 2 ∣ D V ∣ ∣ D ∣ H(D)=-\sum_{v=1}^V\frac{|D_V|}{|D|}log_2\frac{|D_V|}{|D|} H(D)=−∑v=1V∣D∣∣DV∣log2∣D∣∣DV∣
H(D|A)为条件熵,计算公式如下:
H ( D ∣ A ) = ∑ v = 1 V ∣ D V ∣ ∣ D ∣ H ( D V ) = ∑ v = 1 V ∣ D V ∣ ∣ D ∣ ∑ k = 1 k ∣ D i k ∣ ∣ D i ∣ l o g 2 ∣ D i k ∣ ∣ D i ∣ H(D|A)=\sum_{v=1}^V\frac{|D_V|}{|D|}H(D_V)=\sum_{v=1}^V\frac{|D_V|}{|D|}\sum_{k=1}^k\frac{|D_ik|}{|D_i|}log_2\frac{|D_ik|}{|Di|} H(D∣A)=∑v=1V∣D∣∣DV∣H(DV)=∑v=1V∣D∣∣DV∣∑k=1k∣Di∣∣Dik∣log2∣Di∣∣Dik∣
**信息增益越大,表明特征子集 A 包含的有助于分类的信息越多。**所以对于每个候选特征子集,可以基于训练集 D 来计算其信息增益作为评价准则。
将特征子集搜索机制与子集评价机制结合就能得到特征选择方法。
3、特征选择方法
-
过滤式(filter): 先进行特征选择,然后去训练学习器,所以特征选择的过程与学习器无关。相当于先对特征进行过滤操作,然后用特征子集来训练分类器。
-
包裹式(wrapper): 实际上就是一个分类器,直接把最后要使用的分类器作为特征选择的评价函数,对于特定的分类器选择最优的特征子集。
-
嵌入式(embedding): 把特征选择的过程与分类器学习的过程融合一起,在学习的过程中进行特征选择。最常见的使用L1正则化进行特征选择。
本文中使用sklearn中的IRIS(鸢尾花)数据集来对特征选择方法进行说明。IRIS数据集由Fisher在1936年整理,包含4个特征(Sepal.Length(花萼长度)、Sepal.Width(花萼宽度)、Petal.Length(花瓣长度)、Petal.Width(花瓣宽度)),特征值都为正浮点数,单位为厘米。目标值为鸢尾花的分类(Iris Setosa(山鸢尾)、Iris Versicolour(杂色鸢尾),Iris Virginica(维吉尼亚鸢尾))。导入IRIS数据集的代码如下:
from sklearn.datasets import load_iris
#导入IRIS数据集
iris = load_iris()
#特征矩阵
iris.data
#目标向量
iris.target
3.1 过滤式(filter)特征选择
该方法先对数据集进行特征选择,然后再训练学习器。特征选择过程与后续学习器无关。也就是先采用特征选择对初始特征进行过滤,然后用过滤后的特征训练模型。
-
优点是计算时间上比较高效,而且对过拟合问题有较高的鲁棒性;
-
缺点是倾向于选择冗余特征,即没有考虑到特征之间的相关性。
该方法设计了一个相关统计量来度量特征的重要性。
- 该统计量是一个向量,其中每个分量都对应于一个初始特征。特征子集的重要性则是由该子集中每个特征所对应的相关统计量分量之和来决定的。
- 最终只需要指定一个阈值 k,然后选择比 k 大的相关统计量分量所对应的特征即可。也可以指定特征个数 m ,然后选择相关统计量分量最大的 m 个特征。
可用的相关统计量—度量特征,基于不同的相关统计量可以过滤式(filter)特征选择可以分为以下几种方法
3.1.1 Pearson相关系数法
皮尔森相关系数是一种最简单的,能帮助理解特征和响应变量之间关系的方法,该方法衡量的是变量之间的线性相关性,结果的取值区间为 [-1,1] , [-1] 表示完全的负相关(这个变量下降,那个就会上升), [1] 表示完全的正相关, [0] 表示没有线性相关。Pearson Correlation速度快、易于计算,经常在拿到数据(经过清洗和特征提取之后的)之后第一时间就执行。Scipy的pearsonr方法能够同时计算相关系数和p-value,
import numpy as np
from scipy.stats import pearsonr
np.random.seed(0)
size = 300
x = np.random.normal(0, 1, size)
print("Lower noise", pearsonr(x, x + np.random.normal(0, 1, size)))
print("Higher noise", pearsonr(x, x + np.random.normal(0, 10, size)))
Pearson相关系数的一个明显缺陷是,作为特征排序机制,他只对线性关系敏感。如果关系是非线性的,即便两个变量具有一一对应的关系,Pearson相关性也可能会接近 [0] 。
3.1.2卡方经验
经典的卡方检验是检验定性自变量对定性因变量的相关性。假设自变量有N种取值,因变量有M种取值,考虑自变量等于i且因变量等于j的样本频数的观察值与期望的差距,构建统计量:
X 2 = ∑ ( A − E ) 2 E X^2=\sum\frac{(A-E)^2}{E} X2=∑E(A−E)2
不难发现,这个统计量的含义简而言之就是自变量对因变量的相关性。用sklearn中feature_selection库的SelectKBest类结合卡方检验来选择特征的代码如下:
from sklearn.datasets import load_iris
from sklearn.feature_selection import SelectKBest
from sklearn.feature_selection import chi2
iris = load_iris()
X, y = iris.data, iris.target
#选择K个最好的特征,返回选择特征后的数据
X_new = SelectKBest(chi2, k=2).fit_transform(X, y)
print(X_new)
3.1.3 互信息法
经典的互信息也是评价定性自变量对定性因变量的相关性的,互信息公式如下:
为了处理定量数据,最大信息系数法被提出,使用feature_selection库的SelectKBest类结合最大信息系数法来选择特征的代码如下:
from sklearn.feature_selection import SelectKBest
from minepy import MINE
#由于MINE的设计不是函数式的,定义mic方法将其为函数式的,返回一个二元组,二元组的第2项设置成固定的P值0.5
def mic(x, y):
m = MINE()
m.compute_score(x, y)
return (m.mic(), 0.5)
#选择K个最好的特征,返回特征选择后的数据
SelectKBest(lambda X, Y: array(map(lambda x:mic(x, Y), X.T)).T, k=2).fit_transform(iris.data, iris.target)
3.1.4 方差选择法
过滤特征选择法还有一种方法不需要度量特征 x i x_i xi 和类别标签 y y y的信息量。这种方法先要计算各个特征的方差,然后根据阈值,选择方差大于阈值的特征。
例如,假设我们有一个具有布尔特征的数据集,并且我们要删除超过80%的样本中的一个或零(开或关)的所有特征。布尔特征是伯努利随机变量,这些变量的方差由下式给出:
v a r ( x ) = p ( 1 − p ) var(x)=p(1-p) var(x)=p(1−p)
VarianceThreshold是特征选择的简单基线方法。它删除方差不符合某个阈值的所有特征。默认情况下,它会删除所有零差异特征,即所有样本中具有相同值的特征。使用feature_selection库的VarianceThreshold类来选择特征的代码如下:
rom sklearn.feature_selection import VarianceThreshold
#方差选择法,返回值为特征选择后的数据
#参数threshold为方差的阈值
VarianceThreshold(threshold=3).fit_transform(iris.data)
3.2包裹式(wrapper)特征选择
包裹式特征选择直接把最终将要使用的学习器的性能作为特征子集的评价原则。其目的就是为给定学习器选择最有利于其性能、量身定做的特征子集。
-
优点是直接针对特定学习器进行优化,考虑到特征之间的关联性,因此通常包裹式特征选择比过滤式特征选择能训练得到一个更好性能的学习器,
-
缺点是由于特征选择过程需要多次训练学习器,故计算开销要比过滤式特征选择要大得多。
3.2.1 递归特征消除法
递归消除特征法使用一个基模型来进行多轮训练,每轮训练后,消除若干权值系数的特征,再基于新的特征集进行下一轮训练。使用feature_selection库的RFE类来选择特征的代码如下:
from sklearn.feature_selection import RFE
from sklearn.linear_model import LogisticRegression
#递归特征消除法,返回特征选择后的数据
#参数estimator为基模型
#参数n_features_to_select为选择的特征个数
RFE(estimator=LogisticRegression(), n_features_to_select=2).fit_transform(iris.data, iris.target)
3.3 嵌入式(Embedded)特征选择
嵌入式特征选择是将特征选择与学习器训练过程融为一体,两者在同一个优化过程中完成的。即学习器训练过程中自动进行了特征选择。
3.3.1 基于惩罚项的特征选择法
通过L1正则项来选择特征:L1正则方法具有稀疏解的特性,因此天然具备特征选择的特性,但是要注意,L1没有选到的特征不代表不重要,原因是两个具有高相关性的特征可能只保留了一个,如果要确定哪个特征重要应再通过L2正则方法交叉检验。
3.3.2 基于学习模型的特征选择
这种方法的思路是直接使用你要用的机器学习算法,针对每个单独的特征和响应变量建立预测模型。假如某个特征和响应变量之间的关系是非线性的,可以用基于树的方法(决策树、随机森林)、或者扩展的线性模型等。基于树的方法比较易于使用,因为他们对非线性关系的建模比较好,并且不需要太多的调试。但要注意过拟合问题,因此树的深度最好不要太大,再就是运用交叉验证。通过这种训练对特征进行打分获得相关性后再训练最终模型。
参考资料:
1、https://zhuanlan.zhihu.com/p/32749489
2、https://scikitlearn.org/stable/modules/feature_selection.html#feature-selection