白话机器学习算法理论+实战之EM聚类
1. 写在前面
如果想从事数据挖掘或者机器学习的工作,掌握常用的机器学习算法是非常有必要的,比如我之前写过的一篇十大机器学习算法的小总结,在这简单的先捋一捋, 常见的机器学习算法:
- 监督学习算法:逻辑回归,线性回归,决策树,朴素贝叶斯,K近邻,支持向量机,集成算法Adaboost等
- 无监督算法:聚类,降维,关联规则, PageRank等
为了详细的理解这些原理,曾经看过西瓜书,统计学习方法,机器学习实战等书,也听过一些机器学习的课程,但总感觉话语里比较深奥,读起来没有耐心,并且理论到处有,而实战最重要, 所以在这里想用最浅显易懂的语言写一个白话机器学习算法理论+实战系列。
个人认为,理解算法背后的idea和使用,要比看懂它的数学推导更加重要。idea会让你有一个直观的感受,从而明白算法的合理性,数学推导只是将这种合理性用更加严谨的语言表达出来而已,打个比方,一个梨很甜,用数学的语言可以表述为糖分含量90%,但只有亲自咬一口,你才能真正感觉到这个梨有多甜,也才能真正理解数学上的90%的糖分究竟是怎么样的。如果这些机器学习算法是个梨,本文的首要目的就是先带领大家咬一口。
另外还有下面几个目的:
- 检验自己对算法的理解程度,对算法理论做一个小总结
- 能开心的学习这些算法的核心思想, 找到学习这些算法的兴趣,为深入的学习这些算法打一个基础。
- 每一节课的理论都会放一个实战案例,能够真正的做到学以致用,既可以锻炼编程能力,又可以加深算法理论的把握程度。
- 也想把之前所有的笔记和参考放在一块,方便以后查看时的方便。
学习算法的过程,获得的不应该只有算法理论,还应该有乐趣和解决实际问题的能力!
今天是白话机器学习算法理论+实战的第九篇之EM聚类。 听到这个名字,就知道这是一个无监督学习算法了,如果使用基于最大似然估计的模型,模型中存在隐变量的时候,就要用到EM算法去做估计。所以这个算法就是含有隐变量的概率模型参数的极大似然估计法,可能我说的这些话你还听不太懂,什么隐变量,什么极大似然乱七八糟的? 没事,通过今天的学习,就能够快速的掌握EM算法的工作原理,还能理解极大似然,还能最后通过调用工具实现EM算法并完成一个王者荣耀英雄人物的聚类(玩游戏的时候,是不是会遇到对手抢了你擅长的英雄的情况啊, 那你该如何选一个和这个英雄整体实力差不多的呢?)。 哈哈 ,是不是迫不及待了啊? 我们开始吧。
大纲如下:
- 从一个生活场景引出EM算法的核心思想(分菜均匀,你该如何划分?)
- 白话EM算法的工作原理,并举例子说明(抛硬币都玩过吧)
- 看看EM聚类(和KMeans有何不同?)
- EM算法实战 - 对王者荣耀的英雄角色进行聚类(实行聚类之后,我们就可以找到可以互相替换的英雄,也就不怕你的对手选择了你擅长的英雄了)
OK, let’s go!
2. EM算法,还是先从分菜开始吧!
提起EM算法(英文叫做Expectation Maximization,最大期望算法),你可能是第一次听说过, 但是你知道吗? 你在生活中可能不止一次用过这个思想了吧, 正所谓我之前常说的算法来源于生活。 啥? 不信? 那我们看看下面这个场景:
假设,你炒了一份菜,我想要你把它平均分到两个碟子里,该怎么分?
你一听平均分? 总不能拿个称来称一称,计算出一半的分量进行平分吧,如果你真这样做,那不得不承认你是个天才,不用学机器学习了。 反正我感觉大部分人的方法是这样做的:
先分一部分到碟子 A 中,然后再把剩余的分到碟子 B 中,再来观察碟子 A 和 B 里的菜是否一样多,哪个多就匀一些到少的那个碟子里,然后再观察碟子 A 和 B 里的是否一样多……
整个过程一直重复下去,直到份量不发生变化为止。
你是采用的哪种方法呢? 如果是后者,那么恭喜你,你已经初步认识了EM算法,并且和它打交道不止一次了。下面的知识对你来说已经洒洒水了。轻松愉快的往下走吧。
在这个例子中你能看到三个主要的步骤: 初始化参数,观察预期和重新估计。首先是先给每个碟子初始化一些菜量,然后再观察预期,这两个步骤实际上就是期望步骤(Expectation)简称E步。如果结果存在偏差就需要重新估计参数,这个就是最大化步骤(Maximization)简称M步。这两个步骤加起来也就是 EM 算法的过程。

哈哈,是不是豁然开朗了啊,趁着这个时候,看看EM算法的具体工作原理吧。
3. EM算法的工作原理
说到 EM 算法,我们需要先来看一个概念“最大似然”,英文是 Maximum Likelihood,Likelihood 代表可能性,所以最大似然也就是最大可能性的意思。
什么是最大似然呢?
举个例子,有一男一女两个同学,现在要对他俩进行身高的比较,谁会更高呢?根据我们的经验,相同年龄下男性的平均身高比女性的高一些,所以男同学高的可能性会很大。这里运用的就是最大似然的概念。
那还有一个问题:最大似然估计是什么呢?
它指的就是一件事情已经发生了,然后反推更有可能是什么因素造成的。还是用一男一女比较身高为例,假设有一个人比另一个人高,反推他可能是男性。最大似然估计是一种通过已知结果,估计参数的方法。
上面说的这些是啥?EM 算法到底是什么?它和最大似然估计又有什么关系呢?(你这三连问,我有点不知所措)
其实,EM 算法是一种求解最大似然估计的方法,通过观测样本,来找出样本的模型参数。
再回过来看下开头我给你举的分菜的这个例子,实际上最终我们想要的是碟子 A 和碟子 B 中菜的份量,你可以把它们理解为想要求得的模型参数。然后我们通过 EM 算法中的 E 步来进行观察,然后通过 M 步来进行调整 A 和 B 的参数,最后让碟子 A 和碟子 B 的参数不再发生变化为止。
然后,你恍然大悟,哦,原理EM算法就这么简单啊,哈哈,不要太高估自己了, 实际我们遇到的问题,比分菜复杂的多。 不行,那再看看我给你举的下面这个例子:
抛硬币大家都玩过吧,假设我们有 A 和 B 两枚硬币,我们做了 5 组实验,每组实验投掷 10 次,每次只能只有A或者B一枚硬币。 那么我们统计出现每组实验正面的次数,实验结果如下:
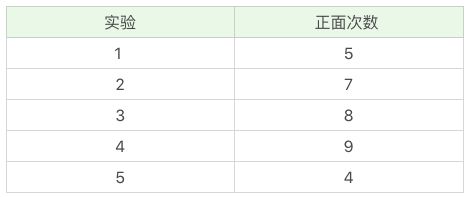
我想问你,你知道,A硬币和B硬币各自正面朝上的概率吗?
怎么样? 蒙了吧, 你说这咋求,每一组实验,我都不知道用的是A或者B抛的。 我怎么算? 那么好,我假设把这个表再给你完善一下:
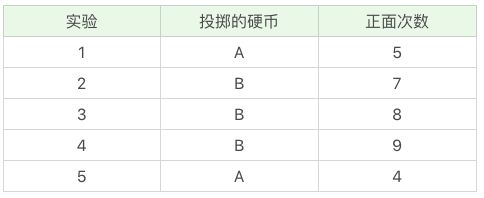
这你能告诉我答案了吧? 你说: 这还不简单, 我们不就可以直接求了,令A正面朝上的概率是θA, B正面朝上的概率是θB,然后:

哈哈, 漂亮! 你知道吗? 一开始我提到这样一句话:
如果使用基于最大似然估计的模型,模型中存在隐变量的时候,就要用到EM算法去做估计
这里的第二列,就是隐含的数据,而A和B就是隐变量。 实际中我们是不知道这一列的,就是开始给你的只有实验组数和正面的次数, 那么你该怎么办呢?
也就是说,我们如果不知道每一组扔的是A还是B,那么我们就无法去估计θA和θB, 而如果想知道每一组扔的是A还是B,我们就必须先知道A和B正面朝上的概率θA和θB,然后利用极大似然的思想,根据每一组实验正面朝上的次数去估计出这一轮究竟用的A还是B。 有点绕哈! 你会发现这是一个鸡生蛋蛋生鸡的问题,无法求解!
那么说了半天,应该怎么办呢? 这里就采用了EM算法的思想。
我先随机初始化一个θA和θB, 有了这两个参数,我们就能按照极大似然估计出每一组用的是A还是B,然后基于每一组用的是A还是B,我们又能按照极大似然反过来计算出θA和θB,然后又能去估计新的用的是A还是B,然后又能计算新的θA和θB,这样一轮轮的下去, 当计算出的新的θA和θB与我们前一轮θA和θB一样的时候,说明这个θA和θB有可能就是真实的值了。这个就是EM初级版。
好了,根据我上面说的,我们看看怎么实行吧。

这里有两个问题需要解答一下:
- 新估计出的θA和θB一定会更接近真实的θA和θB?
答案是:没错,一定会更接近真实的θA和θB,数学可以证明,但这超出了本文的主题,请参阅其他书籍或文章。(这就类似你均匀分菜,总会有分好的那一个点吧)- 迭代一定会收敛到真实的θA和θB吗?
答案是:不一定,取决于θA和θB的初始化值,一般是会的。
其实,上面介绍的这个只是一个初始的版本,为什么这么说呢?因为我们上面第一次计算概率的时候,我们算出:

这时候我们直接取得第一次用硬币A(下面几组实验同理)。
你没有发现,这样做决定太硬,太绝对了吗? 虽然B出现正面次数为5的概率比A的小,但是也不是0啊,就是也有可能出现啊。这时候我们应该考虑进这种可能的情况,那么这时候,第一轮实验用的A的概率就是: 0.246 / (0.246 + 0.015) = 0.9425;用B的概率就是1-0.9425 = 0.0575。
相比于前面的方法,我们按照最大似然概率,直接将第1轮估计为用的硬币A,此时的我们更加谨慎,我们只说,有0.9425的概率是硬币A,有0.0575的概率是硬币B,不再是非此即彼。这样我们在估计θA和θB时,就可以用上每一轮实验的数据,而不是某几轮实验的数据,显然这样会更好一些。
这一步,我们实际上估计的是用A或者B的一个概率分布,这步就称作E步。
这样,每一轮实验,我们会求出这样一个表来,分别有A和B的概率:

然后,我们在结合着统计结果,
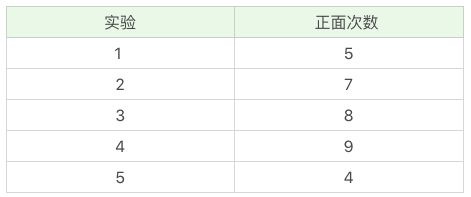
按照最大似然概率的法则重新估计新的θA和θB:
以硬币A为例, 第一轮的正面次数为5相当于 5次正面,5次反面
- 0.9425 * 5 = 4.7125(这是正面)
- 0.9425 * 5 = 4.7125(这是反面)
那么对于硬币A来说, 可以把五轮的表格画成下面的形式:
这样, 新的thetaA = 4.22 / (4.22+7.98)=0.35 这样,改变了硬币A和B的估计方法之后,会发现,新估计的thetaA会更加接近真实的值,因为我们使用了每一轮的数据,而不是某几轮的数据。
PS: 上面这个表我只是为了说明意思,截取过来的一个图,真实数据并不是这样的数据,看第一轮也能看出来,真实数据是我上面计算的那个,按照那个计算方法,计算出每一轮的硬币A的时候正面和反面的数据,硬币B的正面和方面的数据,然后求新的θA和θB会更加准确一些。
这步中,我们根据E步求出了硬币A和B在每一轮实验中的一个概率分布,依据最大似然法则结合所有的数据去估计新的θ1和θ2, 被称作M步。
这个就是进阶版的EM算法。
说到这,EM算法的工作原理可算是介绍完了, 你明白了吗?
简单的总结下上面的步骤:
你能看出 EM 算法中的 E 步骤就是通过旧的参数来计算隐藏变量。然后在 M 步骤中,通过得到的隐藏变量的结果来重新估计参数。直到参数不再发生变化,得到我们想要的结果。
下面,我们看看EM算法聚类的原理,前面介绍过KMeans聚类,同是聚类,有什么区别?
4. EM聚类的工作原理
EM算法一般用于聚类,也就是无监督模型里面,因为无监督学习没有标签(即y值),EM算法可以先给无监督学习估计一个隐状态(即标签),有了标签,算法模型就可以转换成有监督学习,这时就可以用极大似然估计法求解出模型最优参数。其中估计隐状态流程应为EM算法的E步,后面用极大似然估计为M步。
相比于 K-Means 算法,EM 聚类更加灵活,比如下面这两种情况,K-Means 会得到下面的聚类结果。
因为 K-Means 是通过距离来区分样本之间的差别的,且每个样本在计算的时候只能属于一个分类,称之为是硬聚类算法。而 EM 聚类在求解的过程中,实际上每个样本都有一定的概率和每个聚类相关,叫做软聚类算法。
你可以把 EM 算法理解成为是一个框架,在这个框架中可以采用不同的模型来用 EM 进行求解。常用的 EM 聚类有 GMM 高斯混合模型和 HMM 隐马尔科夫模型。GMM(高斯混合模型)聚类就是 EM 聚类的一种。比如上面这两个图,可以采用 GMM 来进行聚类。
和 K-Means 一样,我们事先知道聚类的个数,但是不知道每个样本分别属于哪一类。通常,我们可以假设样本是符合高斯分布的(也就是正态分布)。每个高斯分布都属于这个模型的组成部分(component),要分成 K 类就相当于是 K 个组成部分。这样我们可以先初始化每个组成部分的高斯分布的参数,然后再看来每个样本是属于哪个组成部分。这也就是 E 步骤。
再通过得到的这些隐含变量结果,反过来求每个组成部分高斯分布的参数,即 M 步骤。反复 EM 步骤,直到每个组成部分的高斯分布参数不变为止。
这样也就相当于将样本按照 GMM 模型进行了 EM 聚类。

所以说很多KMeans解决不了的问题,EM聚类是可以解决的。在 EM 框架中,我们将潜在类别当做隐藏变量,样本看做观察值,把聚类问题转化为参数估计问题,最终把样本进行聚类。
最后再多啰嗦一句,EM 算法相当于一个框架,你可以采用不同的模型来进行聚类,比如 GMM(高斯混合模型),或者 HMM(隐马尔科夫模型)来进行聚类。
- GMM 是通过概率密度来进行聚类,聚成的类符合高斯分布(正态分布)。
- 而 HMM 用到了马尔可夫过程,在这个过程中,我们通过状态转移矩阵来计算状态转移的概率。HMM 在自然语言处理和语音识别领域中有广泛的应用。
好了,也说了EM算法聚类的原理了,下面让我们实战吧!
5. EM算法实战 - 王者荣耀英雄的聚类
上面是EM算法的原理,懂了原理之后,趁热打铁,做一个实际的小项目,看看EM算法的威力吧!
5.1 如何使用EM工具包
在 Python 中有第三方的 EM 算法工具包。由于 EM 算法是一个聚类框架,所以你需要明确你要用的具体算法,比如是采用 GMM 高斯混合模型,还是 HMM 隐马尔科夫模型。
我们主要是用GMM,所以需要引入工具包
from sklearn.mixture import GaussianMixture
那么如何创建GMM聚类呢?
gmm = GaussianMixture(n_components=1, covariance_type=‘full’, max_iter=100)来创建, 参数如下:
- n_components:即高斯混合模型的个数,也就是我们要聚类的个数,默认值为 1。如果你不指定 n_components,最终的聚类结果都会为同一个值。
- covariance_type:代表协方差类型。一个高斯混合模型的分布是由均值向量和协方差矩阵决定的,所以协方差的类型也代表了不同的高斯混合模型的特征。协方差类型有 4 种取值:
- covariance_type=full,代表完全协方差,也就是元素都不为 0;
- covariance_type=tied,代表相同的完全协方差;
- covariance_type=diag,代表对角协方差,也就是对角不为 0,其余为 0;
- covariance_type=spherical,代表球面协方差,非对角为 0,对角完全相同,呈现球面的特性。
- max_iter:代表最大迭代次数,EM 算法是由 E 步和 M 步迭代求得最终的模型参数,这里可以指定最大迭代次数,默认值为 100。
创建完GMM聚类器之后,可以传入数据让它进行迭代拟合。
我们使用 fit 函数,传入样本特征矩阵,模型会自动生成聚类器,然后使用 prediction=gmm.predict(data) 来对数据进行聚类,传入你想进行聚类的数据,可以得到聚类结果 prediction。
你能看出来拟合训练和预测可以传入相同的特征矩阵,这是因为聚类是无监督学习,你不需要事先指定聚类的结果,也无法基于先验的结果经验来进行学习。只要在训练过程中传入特征值矩阵,机器就会按照特征值矩阵生成聚类器,然后就可以使用这个聚类器进行聚类了。
5.2如何用 EM 算法对王者荣耀数据进行聚类
首先我们知道聚类的原理是“人以群分,物以类聚”。通过聚类算法把特征值相近的数据归为一类,不同类之间的差异较大,这样就可以对原始数据进行降维。通过分成几个组(簇),来研究每个组之间的特性。或者我们也可以把组(簇)的数量适当提升,这样就可以找到可以互相替换的英雄,比如你的对手选择了你擅长的英雄之后,你可以选择另一个英雄作为备选。
5.2.1 数据集的介绍
看看数据的样子: 数据集在这里下载

这里我们收集了 69 名英雄的 20 个特征属性,这些属性分别是最大生命、生命成长、初始生命、最大法力、法力成长、初始法力、最高物攻、物攻成长、初始物攻、最大物防、物防成长、初始物防、最大每 5 秒回血、每 5 秒回血成长、初始每 5 秒回血、最大每 5 秒回蓝、每 5 秒回蓝成长、初始每 5 秒回蓝、最大攻速和攻击范围等。
5.2.2执行流程
- 首先加载数据源
- 在准备阶段,我们需要对数据进行探索,包括采用数据可视化技术,让我们对英雄属性以及这些属性之间的关系理解更加深刻,然后对数据质量进行评估,是否进行数据清洗,最后进行特征选择方便后续的聚类算法
- 聚类阶段:选择适合的聚类模型,这里我们采用 GMM 高斯混合模型进行聚类,并输出聚类结果,对结果进行分析。
5.2.3 实战操作
- 首先导入包
import pandas as pd
import csv
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.preprocessing import StandardScaler
from sklearn.mixture import GaussianMixture
- 加载数据
# 数据加载,避免中文乱码问题
data_ori = pd.read_csv('dataset/heros.csv', encoding = 'gb18030')
features = [u'最大生命',u'生命成长',u'初始生命',u'最大法力', u'法力成长',u'初始法力',u'最高物攻',u'物攻成长',u'初始物攻',u'最大物防',u'物防成长',u'初始物防', u'最大每5秒回血', u'每5秒回血成长', u'初始每5秒回血', u'最大每5秒回蓝', u'每5秒回蓝成长', u'初始每5秒回蓝', u'最大攻速', u'攻击范围']
data = data_ori[features]
- 数据可视化的探索
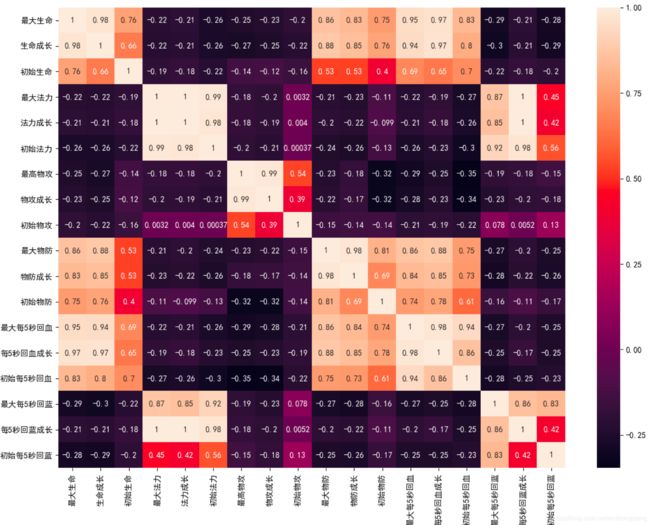
我们将 20 个英雄属性之间的关系用热力图呈现了出来,中间的数字代表两个属性之间的关系系数,最大值为 1,代表完全正相关,关系系数越大代表相关性越大。从图中你能看出来“最大生命”“生命成长”和“初始生命”这三个属性的相关性大,我们只需要保留一个属性即可。同理我们也可以对其他相关性大的属性进行筛选,保留一个。你在代码中可以看到,我用 features_remain 数组保留了特征选择的属性,这样就将原本的 20 个属性降维到了 13 个属性。
# 对英雄属性之间的关系进行可视化分析
# 设置plt正确显示中文
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号
# 用热力图呈现features_mean字段之间的相关性
corr = data[features].corr()
plt.figure(figsize=(14,14))
# annot=True显示每个方格的数据
sns.heatmap(corr, annot=True)
plt.show()
- 特征工程
# 相关性大的属性保留一个,因此可以对属性进行降维
features_remain = [u'最大生命', u'初始生命', u'最大法力', u'最高物攻', u'初始物攻', u'最大物防', u'初始物防', u'最大每5秒回血', u'最大每5秒回蓝', u'初始每5秒回蓝', u'最大攻速', u'攻击范围']
data = data_ori[features_remain]
- 数据规范化
我们能看到“最大攻速”这个属性值是百分数,不适合做矩阵运算,因此我们需要将百分数转化为小数。我们也看到“攻击范围”这个字段的取值为远程或者近战,也不适合矩阵运算,我们将取值做个映射,用 1 代表远程,0 代表近战。然后采用 Z-Score 规范化,对特征矩阵进行规范化。
data[u'最大攻速'] = data[u'最大攻速'].apply(lambda x: float(x.strip('%'))/100)
data[u'攻击范围']=data[u'攻击范围'].map({
'远程':1,'近战':0})
# 采用Z-Score规范化数据,保证每个特征维度的数据均值为0,方差为1
ss = StandardScaler()
data = ss.fit_transform(data)
- 建模并产生结果,写入文件
# 构造GMM聚类
gmm = GaussianMixture(n_components=30, covariance_type='full')
gmm.fit(data)
# 训练数据
prediction = gmm.predict(data)
print(prediction)
# 将分组结果输出到CSV文件中
data_ori.insert(0, '分组', prediction)
## 结果如下:
[28 14 8 9 5 5 15 8 3 14 18 14 9 7 16 18 13 3 5 4 19 12 4 12
12 12 4 17 24 2 7 2 2 24 2 2 24 6 20 22 22 24 24 2 2 22 14 20
14 24 26 29 27 25 25 28 11 1 23 5 11 0 10 28 21 29 29 29 17]
我们采用了 GMM 高斯混合模型,并将结果输出到 CSV 文件中。这里我将输出的结果截取了一段(设置聚类个数为 30):

第一列代表的是分组(簇),我们能看到张飞、程咬金分到了一组,牛魔、白起是一组,老夫子自己是一组,达摩、典韦是一组。聚类的特点是相同类别之间的属性值相近,不同类别的属性值差异大。因此如果你擅长用典韦这个英雄,不防试试达摩这个英雄。同样你也可以在张飞和程咬金中进行切换。这样就算你的英雄被别人选中了,你依然可以有备选的英雄可以使用。
聚类和分类不一样,聚类是无监督的学习方式,也就是我们没有实际的结果可以进行比对,所以聚类的结果评估不像分类准确率一样直观,那么有没有聚类结果的评估方式呢?这里我们可以采用 Calinski-Harabaz 指标,代码如下:
from sklearn.metrics import calinski_harabaz_score
print(calinski_harabaz_score(data, prediction))
指标分数越高,代表聚类效果越好,也就是相同类中的差异性小,不同类之间的差异性大。当然具体聚类的结果含义,我们需要人工来分析,也就是当这些数据被分成不同的类别之后,具体每个类表代表的含义。
另外聚类算法也可以作为其他数据挖掘算法的预处理阶段,这样我们就可以将数据进行降维了。
6. 总结
到这终于写完了, 我的天啊,每次写都是这么多,这可以慢慢的干货啊,虽然多,但真的可以学到东西。 赶紧来总结一下,今天首先从分菜的例子出发,感受了一下EM算法。
然后,我们从抛硬币的例子,知道了初级EM和升级版EM。然后解释了EM的工作原理,EM 算法中的 E 步骤就是通过旧的参数来计算隐藏变量。然后在 M 步骤中,通过得到的隐藏变量的结果来重新估计参数。直到参数不再发生变化,得到我们想要的结果。
接下来,就是对比了EM和KMeans的区别,知道了EM可以解决Kmeans不能解决的一些问题,并且EM是个框架,具体实现包括高斯混合模型和隐马尔可夫模型,后期会具体讲隐马尔可夫。
最后,调用sklearn的EM算法工具完成了一个王者荣耀英雄的聚类任务, 知道了一个衡量聚类结果的函数。
希望通过今天的学习可以对EM算法在感性上有一个了解,至于理性方面, 可以看看西瓜书或者统计学习方法进行深一步的学习了。
最后就是感谢一下陈旸老师,听了他的《数据分析实战45讲》之后,感觉不仅让之前学习的算法理论变得更加的真实,并且还能够活学活用,还能get到认知和思维,哈哈,推荐。
参考:
- 极客时间数据分析实战45讲(上面网格图片的出处和实践项目都是摘自于此)
- 西瓜书EM算法的笔记
- 无监督学习之EM算法
- EM算法原理
PS: 由于统计学习方法中的EM算法还没整理好,所以这里的参考笔记先不放统计学习方法,后期补上。
什么,还没看够? 哈哈,可以看看其他的系列,也同样有趣又能学习到知识
- 白话机器学习算法理论+实战之决策树 - 帮你搞定相亲选择的烦恼
- 白话机器学习算法理论+实战之关联规则 - 带你领略导演拍戏一般会喜欢哪些演员的
- 白话机器学习算法理论+实战之PageRank算法 - 帮你分析与你对象交往的人员之间的关系紧密程度
- 白话机器学习算法理论+实战之AdaBoost算法 - 带你实现三个臭皮匠顶个诸葛亮的故事
- 白话机器学习算法理论+实战之朴素贝叶斯 - 帮你获得上帝的视角
- 白话机器学习算法理论+实战之支持向量机(SVM) - 教你检测是否有乳腺癌
- 白话机器学习算法理论+实战之K近邻算法 - 教你识别手写数字
- 白话机器学习算法理论+实战之KMearns聚类算法 - 帮你完成图像分割
- 白话机器学习算法理论+实战之PCA降维 - 带你玩一下人脸识别的降维